Giải bài tập SGK Toán 9 Bài 1: Sự xác định đường tròn. Tính chất đối xứng của đường tròn

Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.

Phương pháp giải

+) Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm này cùng cách đều một điểm.

+) Sử dụng tính chất của hình chữ nhật: ABCD là hình chữ nhật, hai đường chéo cắt nhau tại O thì ta có \(OA=OB=OC=OD=\dfrac{AC}{2}=\dfrac{BD}{2}\)

+) Định lí Pytago: \(\Delta{ABC}\)vuông tại C thì \(BC^2=AB^2+AC^2.\)

Hướng dẫn giải

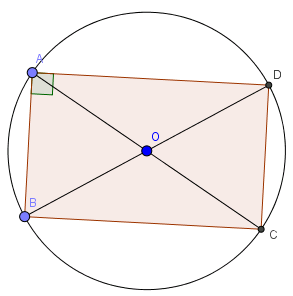
Gọi O là giao điểm của hai đường chéo AC và BD.

Ta có 
\(\left\{ \begin{aligned} & OA=OC,OB=OD \\ & AC=BD \\ \end{aligned} \right.\) (tính chất đường chéo hình chữ nhật)

Suy ra OA = OB = OC = OD

Vậy bốn điểm A, B, C, D thuộc cùng một đường tròn (tâm O, bán kính OA)

Áp dụng định lí Pytago trong tam giác vuông ABC có:
\(AC=\sqrt{A{{B}^{2}}+B{{C}^{2}}}=\sqrt{{{12}^{2}}+{{5}^{2}}}=\sqrt{169}=13\,\left( cm \right)\)

Suy ra bán kính đường tròn là OA = 13 : 2 = 6,5 cm

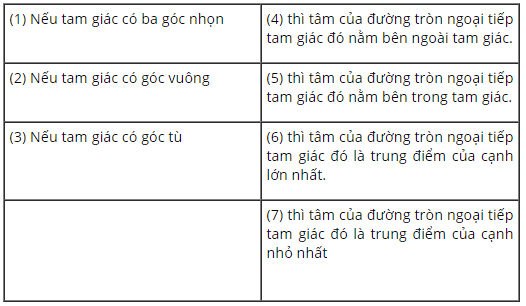
Hãy nối mỗi ô ở cột trái với mỗi ô ở cột phải để được khẳng định đúng.

Phương pháp giải

+) Tâm của đường tròn ngoại tiếp tam giác là giao của ba đường trung trực.

+) Sử dụng tính chất đường trung tuyến trong tam giác vuông: \(\Delta{ABC}\) vuông tại A, có AM là trung tuyến, khi đó: \(AM=BM=CM=\dfrac{BC}{2}\)

Hướng dẫn giải

+) Nối (1) với (5): Vì trong tam giác nhọn, giao của ba đường trung trực nằm bên trong tam giác nên tâm đường tròn ngoại tiếp nằm bên trong ta giác. 

+) Nối (2) với (6): Vì trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó. Tức là trung điểm cạnh huyền cách đều 3 điểm A, B, C

+ Nối (3) với (4): Vì trong tam giác tù, giao của ba đường trung trực nằm bên ngoài tam giác nên tâm đường tròn ngoại tiếp nằm bên ngoài ta giác.

Chứng minh các định lý sau:

a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.

b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

Phương pháp giải

Sử dụng tính chất:

a) Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh đó. 

b) Tam giác có đường trung tuyến ứng với cạnh huyền bằng nửa cạnh đó thì là tam giác vuông.

Hướng dẫn giải

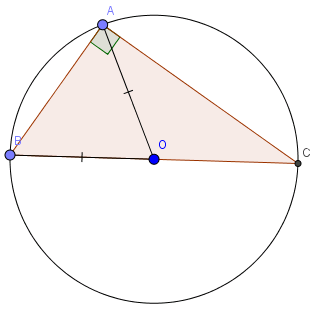
a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.

Ta có OA = OB = OC (tính chất trung tuyến trong tam giác vuông)

Suy ra O là tâm của đường tròn đi qua A, B, C.

Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)

b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:

OA = OB = OC

Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)

Trên mặt phẳng tọa độ Oxy, hãy xác định vị trí của mỗi điểm A(-1; -1), B(-1; -2), C\((\sqrt 2; \sqrt 2)\) đối với đường tròn tâm O bán kính 2.

Phương pháp giải

+) Khoảng cách d từ gốc tọa độ O(0; 0) đến điểm A(x;y) được tính theo công thức \(d=\sqrt{x^{2}+y^{2}}\).            (1)

+) Cho đường tròn tâm O bán kính R, khi đó: 

a) Nếu OM=R thì M nằm trên đường tròn.

b) Nếu OM > R thì M nằm ngoài đường tròn.

c) Nếu OM < R thì M nằm trong đường tròn.

Hướng dẫn giải

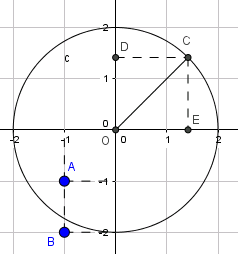
Áp dụng công thức (1) tính khoảng cách từ một điểm đến gốc tọa độ , ta có: 

\(OA=\sqrt {{{( - 1)}^2} + {{( - 1)}^2}} =\sqrt{2}< 2\Rightarrow A\) nằm trong đường tròn (O;2).

\(OB=\sqrt {{{( - 1)}^2} + {{( - 2)}^2}} =\sqrt{5}> 2\Rightarrow B\) nằm ngoài đường tròn (O;2).

\(OC=\sqrt {{{\left( {\sqrt 2 } \right)}^2} + {{\left( {\sqrt 2 } \right)}^2}} =2\Rightarrow C\) nằm trên đường tròn (O;2).

Một tấm bìa hình tròn không còn dấu vết của tâm. Hãy tìm lại tâm của hình tròn đó.

Phương pháp giải

Sử dụng các tính chất: 

+) Giao của ba đường trung trực là tâm đường trong ngoại tiếp tam giác.

+) Trong một đường tròn, các đường kính cắt nhau tại tâm đường tròn.

Hướng dẫn giải

- Gấp tấm bìa sao cho hai phần của hình tròn trùng nhau, nếp gấp là một đường kính.

- Lại gấp như trên theo nếp gấp khác, ta được một đường kính thứ hai. Giao điểm của hai đường kính này là tâm của đường tròn.