Toán 8 Chương 3 Bài 1: Định lí Ta-lét trong tam giác

a) Định nghĩa

- Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.

- Tỉ số của hai đoạn thẳng AB và CD được kí hiệu là \(\dfrac{{AB}}{{C{\text{D}}}}\)

b) Chú ý: Tỉ số của hai đoạn thẳng không phụ thuộc vào các chọn đơn vị đo.

Định nghĩa: Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A'B' và C'D' nếu có tỉ lệ thức

\(\dfrac{{AB}}{{C{\text{D}}}} = \dfrac{{A'B'}}{{C'D'}}\;\;hay\;\;\dfrac{{AB}}{{A'B'}} = \dfrac{{C{\text{D}}}}{{C'D'}}\)

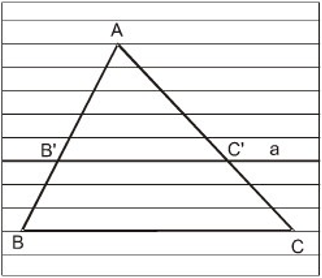
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.

Tổng quát : Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC

Ta có: \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}};\frac{{AB'}}{{BB'}} = \frac{{AC'}}{{C'C}};\frac{{BB'}}{{AB}} = \frac{{CC'}}{{AC}}\)

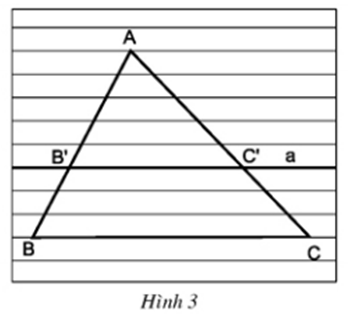
Vẽ tam giác \(ABC\) trên giấy kẻ học sinh như trên hình 3. Dựng đường thẳng \(a\) song song với cạnh \(BC\), cắt hai cạnh \(AB, AC\) theo thứ tự tại \(B'\) và \(C'\).

Đường thẳng \(a\) định ra trên cạnh \(AB\) ba đoạn thẳng \(AB',B'B\) và \(AB\), và định ra trên cạnh \(AC\) ba đoạn thẳng tương ứng là \(AC',C'C\) và \(AC\).

So sánh các tỉ số:

\(a)\,\dfrac{{AB'}}{{AB}}\) và \(\dfrac{{AC'}}{{AC}}\)

\(b)\,\,\dfrac{{AB'}}{{B'B}}\) và \(\dfrac{{AC'}}{{C'C}}\)

\(c)\,\,\dfrac{{B'B}}{{AB}}\) và \(\dfrac{{C'C}}{{AC}}\)

Hướng dẫn giải

\(a)\,\dfrac{{AB'}}{{AB}}=\dfrac{{AC'}}{{AC}}=\dfrac{5}{8}\)

\(b)\,\,\dfrac{{AB'}}{{B'B}}=\dfrac{{AC'}}{{C'C}}=\dfrac{5}{3}\)

\(c)\,\,\dfrac{{B'B}}{{AB}}=\dfrac{{C'C}}{{AC}}=\dfrac{3}{8}\)

Viết tỉ số của các cặp đoạn thẳng có độ dài như sau:

a) \(AB = 5cm\) và \(CD =15 cm\)

b) \(EF = 48 cm\) và \(GH = 16 dm\)

c) \(PQ = 1,2m\) và \(MN = 24 cm\)

Hướng dẫn giải

a) Ta có \(AB = 5cm\) và \(CD = 15 cm\)

 \(\Rightarrow \dfrac{AB}{CD}= \dfrac{5}{15}= \dfrac{1}{3}\).

b) \(EF= 48 cm, GH = 16 dm = 160 cm\)

\( \Rightarrow \dfrac{EF}{GH}= \dfrac{48}{160}= \dfrac{3}{10}\)

c) \(PQ= 1,2m = 120cm, MN= 24cm\)

\(\Rightarrow \dfrac{PQ}{MN} = \dfrac{120}{24} = 5.\)

Cho biết độ dài cùa \(AB\) gấp \(5\) lần độ dài của \(CD\) và độ dài của \(A'B'\) gấp \(12\) lần độ dài của \(CD\). Tính tỉ số của hai đoạn thẳng \(AB\) và \(A'B'\).

Hướng dẫn giải

Độ dài \(AB\) gấp \(5\) lần độ dài \(CD\) nên \(AB= 5CD\).

Độ dài \(A'B'\) gấp \(12\) lần độ dài \(CD\) nên \(A'B'= 12CD\).

\( \Rightarrow \) Tỉ số của hai đoạn thẳng \(AB\) và \(A'B'\) là: 

\(\dfrac{AB}{A'B'}= \dfrac{5CD}{12CD} = \dfrac{5}{12}\)

Câu 1: Viết tỉ số của các cặp đoạn thẳng sau:

a) \(AB = 125cm, CD = 625 cm\);

b) \(EF = 45cm, E’F’ = 13,5dm\);

c) \(MN = 555cm, M’N’ = 999cm\);

d) \(PQ = 10101cm, P’Q’ = 303,03m\).

Câu 2: Đoạn thẳng \(AB\) gấp năm lần đoạn thẳng \(CD\); đoạn thẳng \(A’B’\) gấp bảy lần đoạn thẳng \(CD\).

a. Tính tỉ số của hai đoạn thẳng \(AB\) và \(A’B’\).

b. Cho biết đoạn thẳng \(MN = 505cm\) và đoạn thẳng \(M’N’ = 707cm\), hỏi hai đoạn thẳng \(AB , A’B’\) có tỉ lệ với hai đoạn thẳng \(MN\) và \(M’N’\) hay không?

Câu 3: Cho hình thang \(ABCD\) có \(AB // CD\) và \(AB < CD\).

Đường thẳng song song với đáy \(AB\) cắt các cạnh bên \(AD, BC\) theo thứ tự tại \(M\) và \(N.\)

Chứng minh rằng:

a. \(\displaystyle{{MA} \over {AD}} = {{NB} \over {BC}}\)

b. \(\displaystyle{{MA} \over {MD}} = {{NB} \over {NC}}\)

c. \(\displaystyle{{MD} \over {DA}} = {{NC} \over {CB}}\)

HD: Kéo dài các tia \(DA, CB\) cắt nhau tại \(E\) (h.3), áp dụng định lí Ta-lét trong tam giác và tính chất của tỉ lệ thức để chứng minh.

Câu 4: Cho tam giác \(ABC\). Từ điểm \(D\) trên cạnh \(BC\), kẻ các đường thẳng song song với các cạnh \(AB\) và \(AC\), chúng cắt các cạnh \(AC\) và \(AB\) theo thứ tự tại \(F\) và \(E\)

Chứng minh rằng: \(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}} = 1\)

Câu 1: Dựa vào các yếu tố trên hình vẽ là áp dụng định lí Talet, ta được:

A. x=1

B. x=5

C. x=2

D. x=1,5

Câu 2: Chỉ ra một tỉ số sai nếu ta áp dụng định tí Talet

A. \(\frac{LC}{CB}=\frac{LK}{LA}\)

B. \(\frac{IB}{IK}=\frac{IA}{ID}\)

C. \(\frac{IB}{ID}=\frac{IA}{IK}\)

D. \(\frac{KA}{KL}=\frac{KD}{KC}\)

Câu 3: Cho \(\frac{AB}{A'B'}=\frac{CD}{C'D'}\) (1)

(1) <=> AB.C'D'=A'B'.CD (I)

(2) <=> \(\frac{AB}{CD}=\frac{A'B'}{C'D'}\) (II)

A.(I) và (II) đều sai 

B.(I) và (II) đều đúng 

C.Chỉ có (I) đúng 

D.Chỉ có (II) đúng 

Câu 4: Cho các đoạn thẳng: AB=6cm,CD=4cm,PQ=8cm,EF=10cm,MN=25mm,RS=15mm.Hãy chọn phát biểu đúng trong các phát biểu sau: 

A. Hai đoạn thẳng AB và PQ tỉ lệ với hai đoạn thẳng EF và RS

B. Hai đoạn thẳng AB va RS tỉ lệ với hai đoạn thẳng EF và MN

C. Hai đoạn thẳng CD và AB tỉ lệ với hai đoạn thẳng PQ và EF

D. Cả 3 câu trên đều sai 

Câu 5: Cho các đoạn thẳng: AB=8cm,CD=6cm,MN=12mm,PQ=x.Tìm x để Ab và CD tỉ lệ với MN và PQ

A. x=18mm

B. x=9cm

C. x=0,9cm

D. Cả a,b,c đều sai

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Tỉ số của hai đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo.
• Tỉ số hai đoạn thẳng không phụ thuộc vào cách chọn đơn vị đo (miễn là khi đo chỉ cần chọn cùng một đơn vị đo).
• Học sinh nắm vững về đoạn thẳng tỉ lệ và nội dung của định lý Talet, vận dụng định lý vào việc tìm ra các tỉ số bằng nhau trên hình vẽ trong SGK.