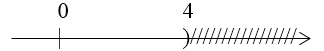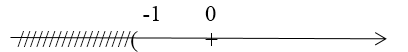Toán 8 Ôn tập chương 4: Bất phương trình bậc nhất một ẩn

Bất đẳng thức là hệ thức có dạng \(a > b\) hoặc \(a < b,a \ge b,a \le b\)

a. Tính chất cộng cùng một số vào hai vế của bất đẳng thức

Khi cộng cùng một số vào hai vế của một bất đẳng thức, ta được một bất đẳng thức mới cùng chiều với hai bất đẳng thức đã cho \( a > b \Rightarrow a + c > b + c\)

b. Tính chất nhân cùng một số vào hai vế của bất đẳng thức

+) Khi nhân cả hai vế của một bất đẳng thức với cùng một số dương, ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

Với \(a > b\)  và \(c > 0 \Rightarrow a.c > b.c\)

+) Khi nhân cả hai vế của một bất đẳng thức với cùng một số âm, ta được một bất đẳng thức mới cùng chiều với bất đẳng thức đã cho.

Với \(a > b\) và \( c < 0 \Rightarrow a.c < b.c\)

c. Tính chất bắc cầu

Nếu a > b và b > c thì a > c

Chú ý: Bất đẳng thức Cô-si

Trung bình cộng của hai số không âm lớn hơn hoặc bằng trung bình nhân của chúng.

\(\dfrac{{a + b}}{2} \ge \sqrt {ab} \)  với \(a \ge 0;b \ge 0\)

Số x = a gọi là nghiệm của một bất phương trình nếu ta thay x = a vào bất phương trình thì được một bất đẳng thức đúng.

Tập hợp tất cả các nghiệm của một bất phương trình gọi là tập nghiệm của bất phương trình. Giải bất phương trình là tìm tập nghiệm của bất phương trình đó.

Bất phương trình tương đương: Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm.

Bất phương trình dạng \(ax + b > 0\) (hoặc \(ax + b < 0,ax + b \ge 0,ax + b \le 0\)) trong đó \(a\) và \(b\) là hai số đã cho, \(a \ne 0\), gọi là bất phương trình bậc nhất một ẩn.

Quy tắc chuyển vế: Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta phải đổi dấu hạng tử đó.

Quy tắc nhân với một số: Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:

+ Giữ nguyên chiều bất phương trình nếu số đó dương;

+ Đổi chiều bất phương trình nếu số đó âm.

Nhắc lại:.

\(\left| a \right| = \left\{ \begin{array}{l}a\;\;khi\;\;a \ge 0\\ - a\;\;khi\;\;a < 0\end{array} \right..\)

Để giải phương trình chứa dấu giá trị tuyệt đối (GTTĐ) dạng \(\left| {A\left( x \right)} \right| = B\left( x \right)\), ta khử dấu GTTĐ bằng cách xét 2 trường hợp :

- Trường hợp 1: \( \left\{ \begin{array}{l}A\left( x \right) \ge 0\\A\left( x \right) = B\left( x \right)\end{array} \right.\)

- Trường hợp 2: \(\left\{ \begin{array}{l}A\left( x \right) < 0\\ - A\left( x \right) = B\left( x \right)\end{array} \right.\)

+) Với phương trình dạng \(\left| {A\left( x \right)} \right| = m\)  với \(m > 0\), ta có:

\(\left| {A\left( x \right)} \right| = m \Leftrightarrow A\left( x \right) = m\) hoặc \(A\left( x \right) =  - m\)

+) Với phương trình dạng \(\left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right|\) ta có:

\( \left| {A\left( x \right)} \right| = \left| {B\left( x \right)} \right|  \Leftrightarrow A\left( x \right) = B\left( x \right)\) hoặc \(A\left( x \right) =  - B\left( x \right)\)

Cho \(m > n\), chứng minh

a) \(m + 2 > n +2\)

b) \(-2m < -2n\)

Hướng dẫn giải

a) Ta có \(m > n\)

Cộng hai vế bất đẳng thức \(m > n\) với \(2\) ta được:

\( m + 2 > n + 2\) (điều phải chứng minh).

b) Ta có \(m > n\)

Nhân hai vế bất đẳng thức \(m > n\) với \((-2)\) ta được:

\(- 2m < - 2n\) (điều phải chứng minh)

Giải các bất phương trình và biểu diễn tập nghiệm trên trục số:

a) \(x - 1 < 3\)

b) \(x + 2  > 1\)

Hướng dẫn giải

a) \(x - 1 < 3  ⇔ x < 1 + 3  ⇔ x < 4\)

Vậy tập nghiệm \(S = \left\{ {x \,|\,x < 4} \right\}\)

Biểu diễn trên trục số:

b) \(x +2 > 1  ⇔ x > 1 – 2  ⇔ x > -1\)

Vậy tập nghiệm  \(S = \left\{ {x \,|\,x > -1} \right\}\)

Biểu diễn trên trục số:

Giải các bất phương trình:

a) \(3 \leqslant \dfrac{{2x + 3}}{5}\)

b) \(\dfrac{{4x - 5}}{3} > \dfrac{{7 - x}}{5}\)

Hướng dẫn giải

a) \(3 \leqslant \dfrac{{2x + 3}}{5}\)

\(\Leftrightarrow 5.3 \leqslant 5.\dfrac{{2x + 3}}{5}\)

\(\Leftrightarrow 15 \le 2x + 3\)

\(⇔15 - 3 \le 2x \)

\(\Leftrightarrow 12 \le 2x\)

\(\Leftrightarrow 6 \le x\)

\(\Leftrightarrow x \ge 6\)

Vậy nghiệm của bất phương trình là: \(x \ge 6\)

b) \(\dfrac{{4x - 5}}{3} > \dfrac{{7 - x}}{5}\)

\(\Leftrightarrow 15.\dfrac{{4x - 5}}{3} > 15.\dfrac{{7 - x}}{5}\)

\(\Leftrightarrow 5\left( {4x - 5} \right) > 3\left( {7 - x} \right)\)

\(⇔20x – 25 > 21 – 3x\)

\(⇔20x + 3x > 21 + 25\)

\(⇔23x > 46\)

\(⇔x > 46 : 23\)            

\(⇔x > 2\) 

Vậy nghiệm của bất phương trình là: \(x > 2\)    

Tìm x sao cho:

a) Giá trị của biểu thức \(x + 3\) nhỏ hơn giá trị của biểu thức \(4x - 5\);

b) Giá trị của biểu thức \(2x +1\) không nhỏ hơn giá trị của biểu thức \(x + 3\);

Hướng dẫn giải

a) Ta có bất phương trình: \(x + 3 < 4x - 5\)

\(⇔x - 4x < -5 - 3\)

\(⇔-3x < -8\)

\(⇔x > \dfrac{8}{3}\)

Vậy để cho \(x + 3\) nhỏ hơn \(4x - 5\) thì \(x >\dfrac{8}{3}\) .

b) Ta có bất phương trình: \(2x +1 ≥ x + 3\)

\(⇔  2x - x ≥ 3 - 1\) 

\(⇔ x ≥ 2\) 

Vậy để cho \(2x +1\) không nhỏ hơn giá trị của biểu thức \(x + 3\) thì \(x ≥ 2\)

Câu 1: Cho \(a > b\), chứng tỏ

a) \(3a + 5 > 3b + 2\) ;

b) \(2 - 4a < 3 - 4b\).

Câu 2: 

a) Chứng tỏ \(2,99\) là nghiệm của bất phương trình \(3 > x\). Hãy kể ra ba số lớn hơn \(2,99\) mà cũng là nghiệm của bất phương trình đó.

b) Chứng tỏ \(4,01\) là nghiệm của bất phương trình \(4 < x\). Hãy kể ra ba số nhỏ hơn \(4,01\) mà cũng là nghiệm của bất phương trình đó.

Câu 3: Giải các bất phương trình và biểu diễn tập nghiệm của chúng trên trục số:

a) \(2\left( {3x - 1} \right) - 2x < 2x + 1\;;\)

b) \(4x - 8 \ge 3\left( {3x - 2} \right) + 4 - 2x.\)

Câu 4: Giải các bất phương trình :

a) \(\displaystyle2x + 1,4 < {{3x - 7} \over 5}\)

b) \(\displaystyle1 + {{1 + 2x} \over 3} > {{2x - 1} \over 6} - 2\)

Câu 1: So sánh \(m^{3}\) và \(m^{2}\) với 0 < m < 1.

A. \(m^{2} > m^{3}\)

B. \(m^{2} < m^{3}\)

C. \(m^{2} = m^{3}\)

D. không so sánh được

Câu 2: Phương trình |x − 1| + |x − 3| = 2x − 1 có số nghiệm là

A. 2     

B. 1

C. 3    

D. 0.

Câu 3: Cho a > b, c > d. Khẳng định nào sau đây đúng?

A. a + d > b + c

B. a + c > b + d

C. b + d > a + c

D. a + b > c + d

Câu 4: Nghiệm nhỏ nhất của phương trình |2 + 3x| = |4x − 3| là

A. \(\frac{1}{7}\)

B. 5

C. -\(\frac{1}{7}\)

D. -5

Câu 5: Cho a > b. Khẳng định nào sau đây đúng?

A. - 3a - 1 > - 3b - 1

B. - 3(a - 1) < - 3(b - 1)

C. - 3(a - 1) > - 3(b - 1)

D. 3(a - 1) < 3(b - 1)

Qua bài học này, các em nắm được một số nội dung chính như sau: 

• Nắm được liên hệ giữa thứ tự và phép nhân , tính chất bắc cầu của thứ tự vận dụng vào giải các bài tập
• Rèn luyện cách trình bày bài tập .
• Vận dụng vào thực tế đời sống