Toán 8 Chương 3 Bài 4: Khái niệm hai tam giác đồng dạng

Tam giác A'B'C' gọi là đồng dạng với tam giác AB nếu:

\(\begin{array}{l} \widehat {A'} = \widehat A;\,\,\,\,\widehat {B'} = \widehat B;\,\,\,\,\widehat {C'} = \widehat C;\\ \frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}}. \end{array}\)

Kí hiệu:\(\Delta A'B'C' \sim \Delta ABC\)

Tỉ số các cạnh tương ứng là \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\) gọi là tỉ số đồng dạng.

Lưu ý: Khi viết kí hiều đồng dạng ta viết theo thứ tự các cặp đỉnh tương ứng.

Hai tam giác \(A'B'C'\) và \(ABC\) đồng dạng có một số tính chất:

\(∆ABC \) đồng dạng \( ∆A'B'C'\)

Nếu \(∆A'B'C'\) đồng dạng \( ∆ABC\) thì \( ∆ABC\) đồng dạng \(∆A'B'C'\)

Nếu \(∆A'B'C'\) đồng dạng \( ∆A"B"C" \) và \(∆A"B"C"\) đồng dạng \( ∆ABC\) thì \(∆A'B'C' \) đồng dạng \( ∆ABC\).

Định lí:

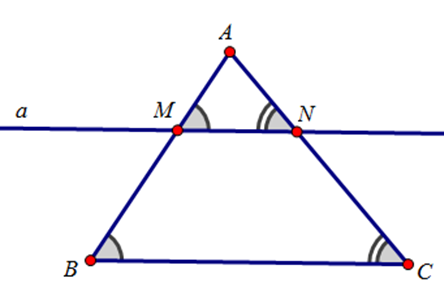
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác ban đầu.

Định lí cũng đúng cho trường hợp đường thẳng a cắt phần kéo dài của hai tam giác song song với cạnh còn lại.

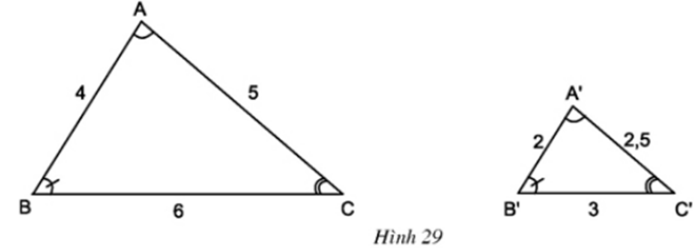
Cho hai tam giác \(ABC\) và \(A’B’C’\) (h.29)

Nhìn vào hình vẽ hãy viết các cặp góc bằng nhau.

Tính các tỉ số \(\dfrac{{A'B'}}{{AB}},{\kern 1pt} {\kern 1pt} \dfrac{{B'C'}}{{BC}},{\kern 1pt} {\kern 1pt} \dfrac{{C'A'}}{{CA}}\) rồi so sánh các tỉ số đó

Hướng dẫn giải

Các cặp góc bằng nhau:

\(\eqalign{& \widehat A = \widehat {A'},\,\,\widehat B = \widehat {B'},\,\,\widehat C = \widehat {C'}  \cr & {{A'B'} \over {AB}} = {2 \over 4} = {1 \over 2}  \cr & {{A'C'} \over {AC}} = {{2,5} \over 5} = {1 \over 2}  \cr & {{B'C'} \over {BC}} = {3 \over 6} = {1 \over 2}  \cr &  \Rightarrow {{A'B'} \over {AB}} = {{A'C'} \over {AC}} = {{B'C'} \over {BC}} \cr} \)

a) Nếu \(ΔA’B’C’ = ΔABC\) thì tam giác \(A’B’C’\) có đồng dạng với tam giác \(ABC\) không ? Tỉ số đồng dạng là bao nhiêu ?

b) Nếu \(ΔA’B’C’\) đồng dạng \(ΔABC\) theo tỉ số \(k\) thì \(ΔABC\) đồng dạng \(ΔA’B’C’\) theo tỉ số nào ?

Hướng dẫn giải

a) Vì \(ΔABC=ΔA’B’C’\) nên \(AB=A'B';AC=A'C';BC=B'C'\) và \(\widehat A=\widehat {A'};\widehat B=\widehat {B'};\)\(\widehat C=\widehat {C'}\) 

Nên \(ΔABC\) đồng dạng \(ΔA’B’C’\) theo tỉ số đồng dạng \(k =\dfrac {AB}{A'B'}= 1\).

b) Nếu \(ΔA’B’C’\) đồng dạng \(ΔABC\) theo tỉ số \(k\) thì ta có: \(\dfrac {A'B'}{AB}=k\) nên \(ΔABC\) đồng dạng \(ΔA’B’C’\) theo tỉ số \(\dfrac {AB}{A'B'}=\dfrac{1}{k}\). 

Cho tam giác \(ABC\). Kẻ đường thẳng \(a\) song song với cạnh \(BC\) và cắt hai cạnh \(AB,AC\) theo thứ tự tại \(M\) và \(N\). Hai tam giác \(AMN\) và \(ABC\) có các góc và các cạnh tương ứng như thế nào?

Hướng dẫn giải

Xét tam giác \(ABC\) có \(MN//BC\)

Hai tam giác \(AMN\) và \(ABC\) có:

\(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị).

\(\widehat {BAC}\) là góc chung.

Mặt khác, theo hệ quả của định lí Ta-lét, hai tam giác \(AMN\) và \(ABC\) có ba cặp cạnh tương ứng tỉ lệ;

\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} = \dfrac{{MN}}{{BC}}\)

Câu 1: Cho hai tam giác \(A’B’C’\) và \(ABC\) đồng dạng với nhau theo tỉ số \(k.\) Chứng minh rằng tỉ số chu vi của hai tam giác cũng bằng \(k.\)

Câu 2: Tam giác \(ABC\) có \(AB = 3cm, BC = 5cm,\) \(CA = 7cm.\)

Tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\) có cạnh nhỏ nhất là \(4,5cm.\)

Tính các cạnh còn lại của tam giác \(A’B’C’.\)

Câu 3: Cho tam giác \(ABC\) có \(AB = 16,2cm, BC = 24,3cm,\) \(AC = 32,7cm.\) Tính độ dài các cạnh của tam giác \(A’B’C’\), biết rằng tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\) và:

a) \(A’B’\) lớn hơn cạnh \(AB\) là \(10,8cm;\)

b) \(A’B’\) bé hơn cạnh \(AB\) là \(5,4cm.\)

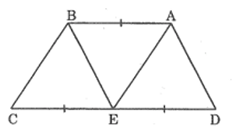
Câu 4: Hình thang \(ABCD\; (AB // CD)\) có \(CD = 2AB.\) Gọi \(E\) là trung điểm của \(DC\) (h21). Chứng minh rằng ba tam giác \(ADE, ABE\) và \(BEC\) đồng dạng với nhau từng đôi một. (Chú ý viết các đỉnh của hai tam giác đồng dạng theo thứ tự tương ứng với nhau).

Câu 1: Chọn câu trả lời đúng 

\(\Delta HKI\sim \Delta EFG\) có hk=5cm,KI=7cm,HI=8cm,EF=2,5cm.Ta có:

A. EG=3,5cm

B. EG=16cm

C. EG=4cm

D. EG=14cm

Câu 2: \(\Delta MNP\sim \Delta EGF\). Phát biểu nào sau đây là sai:

A. \(\widehat{M}=\widehat{E}\)

B. \(\frac{MN}{EG}=\frac{MP}{EF}\)

C. \(\frac{NP}{MP}=\frac{EG}{FG}\)

D. \(\frac{MN}{NP}=\frac{EG}{FG}\)

Câu 3: Tam giác ABC và XYZ đồng dạng, A tương ứng với X,B với Y.Biết AB=3cm, BC=4 và XY=5, vậy YZ bằng:

A. \(3\frac{3}{4}\)

B.6

C.\(6\frac{1}{4}\)

D.\(6\frac{2}{3}\)

Câu 4: Cho hình bình hành ABCD với góc ABC =120, AB=16 và BC=10. Kéo dài CD một đoạn DE=4.Gọi F là giao điểm của AD và BE, độ dài FD gần nhất với:

A. 1

B. 2

C. 3

D. 4

Câu 5: Cho \(\Delta MNP\sim \Delta DEF\) ta có:

A. \(\frac{MN}{DE}=\frac{MP}{EF}\)

B. \(\frac{NP}{MN}=\frac{EF}{DE}\)

C.cả a,b đều đúng 

D. cả a,b đều sai 

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm chắc định nghĩa về 2 tam giác đồng dạng, t/c tam giác đồng dạng, ký hiệu đồng dạng, tỷ số đồng dạng.
• Hiểu được các bước chứng minh định lý.
• Vận dụng định lý để chứng minh tam giác đồng dạng, dựng tam giác đồng dạng với tam giác cho trước theo tỷ số đồng dạng.