Toán 8 Chương 3 Bài 9: Ứng dụng thực tế của tam giác đồng dạng

Giả sử cần phải xác định chiều cao của một tòa nhà, của một ngọn tháp hay của một cây nào đó, ta có thể làm như sau:

Tiến hành đo đạc

• Đặt cọc AC đứng thẳng trên đó có gắn thước ngắm quay được quanh một cái chốt của cọc.
• Điều chỉnh thước ngắm sao cho hướng thước đi qua đỉnh C' của cây (hoặc tháp), sau đó xác định giao điểm B của đường thẳng CC' và AA'.
• Đo khoảng cách BA và BA'.

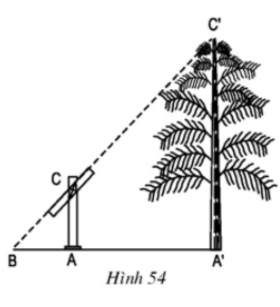
Tính chiều cao cây (hoặc tháp)

Ứng dụng tam giác đồng dạng, ta có: \(\Delta ABC \sim \Delta A'BC'\) với tỉ số đồng dạng \(k=\frac{AC}{A'C'}\)

=> \(A'C'=k.AC\)

Giả sử phải đo khoảng cách AB trong đó địa điểm A có ao hồ bao bọc không thể tới được.

Tiến hành đo đạc

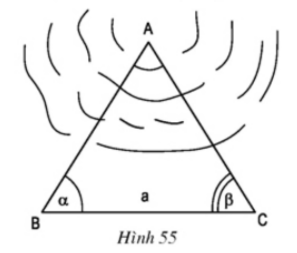
Chọn một khoảng đất bằng phẳng rồi vạch một đoạn BC và đo độ dài của nó (BC = a).

Dùng thước đo góc (giác kế) đo các góc: \(\widehat{ABC}=\alpha ,\widehat{ACB}=\beta\)

Tính khoảng cách AB

• Vẽ trên giấy tam giác A'B'C' sao cho: \(B'C'=a';\widehat{B'}=\alpha ,\widehat{C'}=\beta\)
• Khi đó, \(\Delta ABC \sim \Delta A'B'C'\) theo tỉ số đồng dạng \(k=\frac{AB}{A'B'}\)
• Thay số vào ta tính được AB.   

Ghi chú

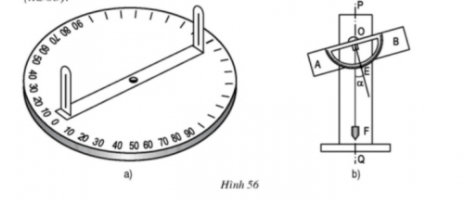
khi đo góc ta dùng giác kế. Giác kế cho phép ta xác định được độ lớn của một góc tuỳ . Có hai loại giác kế: Giác kế ngang (h.56a) và giác kế đứng (h.56b).

Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao 2m và đặt xa cây 15m. Sau khi người ấy lùi ra xa cách cọc 0,8m thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân đến mắt người ấy là 1,6m?

Hướng dẫn giải

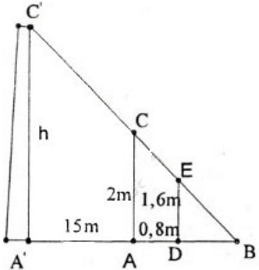
Gọi chiều cao của cây là h = A'C' và chọn một cọc tiêu AC = 2m.

Khoảng cách từ chân đến mắt người đo là DE = 1,6m.

Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.

Ta có: AC // DE (cùng vuông góc với AB)

=> \(\Delta ABC \sim \Delta DEB\) (định lí)

=> \(\frac{DB}{AB}=\frac{DE}{AC}=\frac{1,6}{2}=\frac{4}{5}\)

=> \(\frac{AB-DB}{AB}=\frac{5-4}{5}\)

=> \(\frac{AD}{AB}=\frac{1}{5}=>AB=5.AD=5.0,8=4(m)\)

=> \(A'B=AA'+AB=15+4=19(m)\)

Ta có: AC // A'C'

=> \(\Delta ABC \sim \Delta A'BC'\) (định lí)

=> \(\frac{AB}{A'B}=\frac{AC}{A'C'}\)

=> \(\frac{4}{19}=\frac{2}{A'C'}\)

=> \(A'C'=\frac{2.19}{4}=9,5(m)\)

Vậy chiều cao của cây là 9,5m.

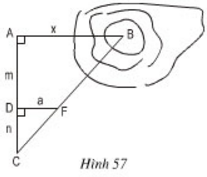
Để đo khoảng cách giữa hai điểm A và B, trong đó B không tới được, người ta tiến hành đo và tính khoảng cách AB như hình 57; AB // DF; AD = m; DC = n; DF = a.

a) Em hãy nói rõ cách đo như thế nào.

b) Tính độ dài x của khoảng cách AB.

Hướng dẫn giải

a) Cách đo

Chọn thêm hai điểm D và C sao cho A, D, C thẳng hàng và AC ⊥ AB.

Chọn điểm F sao cho C, F, B thẳng hàng và DF ⊥ AC.

Đo: AD = m; DC = n; DF = a.

b) Ta có: ∆CDF ∽ ∆CAB (DF // AB)

=> \(\frac{DF}{AB}=\frac{CD}{CA} = > AB = \frac{DF.CA}{CD}= \frac{a(m+n)}{m}\)

Vậy \( x= \frac{DF.CA}{CD}= \frac{a(m+n)}{m}\)

Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước AC được chia đến 1mm và gắn với một bản kim loại hình tam giác ABD, khoảng cách BC = 10mm.

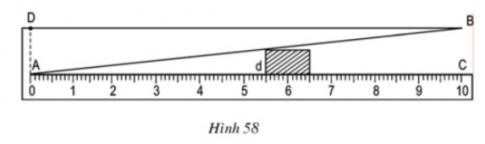
Muốn đo bề dày của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt của thước AC). Khi đó, trên thước AC ta đọc được "bề dày" d của vật (trên hình vẽ ta có có d = 5,5mm).

Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi các vạch trên thước AC (d ≤ 10mm)

Câu 1: Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. ΔABD đồng dạng với tam giác nào dưới đây?

A. ΔAEG.        

B. ΔABC

C. Cả A và B      

D. Không có tam giác nào.

Câu 2: Tỉ số các cạnh bé nhất của 2 tam giác đồng dạng bằng \(\frac{2}{5}\). Tính chu vi p, p′ của 2 tam giác đó, biết p′ − p = 18?

A. p = 12; p′ = 30

B. p = 30; p′ = 12

C. p = 30; p′ = 48

D. p = 48; p′ = 30

Câu 3: Cho tam giác ABC có AB = 9 cm, AC = 16 cm, BC = 20 cm. Khi đó

A. \(\widehat{B} = \frac{\widehat{A}}{3}\)

B. \(\widehat{B} = \frac{2\widehat{A}}{3}\)

C. \(\widehat{B} = \frac{\widehat{A}}{2}\)

D. \(\widehat{B} = \widehat{C}\)

Câu 4: Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC.

Tính các độ dài BD ,BC biết AB = 2cm, AD = 3cm, CD = 8cm

A. BD = 5 cm; BC = 6 cm.

B. BD = 6 cm; BC = 4 cm.

C. BD = 6 cm; BC = 6 cm.

D. BD = 4 cm; BC = 6 cm.

Câu 5: Cho hình bình hành ABCD, điểm F nằm trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn câu đúng nhất.

A. ΔBFE ∽ ΔDEA

B. ΔDEG ∽ ΔBAE  

C. \(AE^{2} = GE.EF\)

D. Cả A, B, C đều đúng.

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm chắc nội dung bài toán thực hành (đo gián tiếp chiều cao của vật, đo khoảng cách giữa hai điểm trong đó có một điểm không thể tới được)
• Nắm chắc các bước tiến hành đo đạt và tính toán trong từng trường hợp, chuẩn bị cho các tiết thực hành tiếp theo.