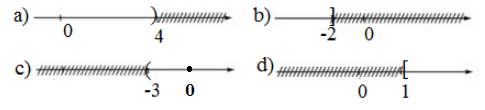Toán 8 Chương 4 Bài 3: Bất phương trình một ẩn

Bất phương trình ẩn \(x \) là hệ thức \(A(x) > B(x)\) hoặc \(A(x) < B(x)\) hoặc \(A(x) ≥ B(x)\) hoặc \(A(x) ≤ B(x)\).

Trong đó: \(A(x)\) gọi là vế trái; \(B(x)\) gọi là vế phải của bất phương trình.

Nghiệm của bất phương trình là giá tri của ẩn thay vào bất phương trình ta được một khẳng định đúng.

Tập hợp tất cả các nghiệm của bất phương trình được gọi là tập nghiệm của bất phương trình đó.

Hai bất phương trình tương đương là hai bất phương trình có cùng tập nghiệm,

Kí hiệu: "\( \Leftrightarrow \)" đọc là tương đương.

a) Hãy cho biết vế trái, vế phải của bất phương trình \({x^2} \leqslant 6x - 5\)      (1)

b) Chứng tỏ các số \(3; 4\) và \(5\) đều là nghiệm, còn số \(6\) không phải là nghiệm của bất phương trình vừa nêu.

Hướng dẫn giải

a) Vế trái của bất phương trình là: \({x^2}\). Vế phải của bất phương trình là: \(6x -5\)

b) Thay  x = 3 vào bất phương trình (1) ta được:

\({3^2} \leqslant 6.3 - 5 \Rightarrow 9 \leqslant 13\) là khẳng định đúng nên \(x = 3\) là nghiệm của bất phương trình (1).

Thay \(x = 4\) vào bất phương trình (1) ta được:

\({4^2} \leqslant 6.4 - 5 \Rightarrow 16 \leqslant 19\) là khẳng định đúng nên \(x = 4\) là nghiệm của bất phương trình (1).

Thay \(x = 5\) vào bất phương trình (1) ta được:

\({5^2} \leqslant 6.5 - 5 \Rightarrow 25 \leqslant 25\) là khẳng định đúng nên \(x = 5\) là nghiệm của bất phương trình (1).

Thay \(x = 6\) vào bất phương trình (1) ta được:

\({6^2} \leqslant 6.6 - 5 \Rightarrow 36 \leqslant 31\) là khẳng định sai nên \(x = 6\) không là nghiệm của bất phương trình (1).

Hãy cho biết vế trái, vế phải và tập nghiệm của bất phương trình \(x > 3\), bất phương trình \(3 < x\) và phương trình \(x = 3\).

Hướng dẫn giải

- Bất phương trình \(x > 3\) có \(VT = x; VP = 3\)

Nghiệm của bất phương trình \(x > 3\) là tập hợp các số lớn hơn \(3\), tức là tập hợp \(\{x|x > 3\}\).

- Bất phương trình \(3 < x\) có \(VT = 3; VP = x\)

Nghiệm của bất phương trình \(3 < x\) là tập hợp các số lớn hơn \(3\), tức là tập hợp \(\{x|x > 3\}\)

- Bất phương trình \(x = 3\) có \(VT = x; VP = 3\)

Nghiệm của bất phương trình \(x = 3\) là \(\{3\}\)

Trong đó: VT là vế trái

               VP là vế phải.

Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau:

a) \(x < 4\);          b) \(x ≤ -2\);           c) \(x > -3\);              d) \(x  ≥ 1\).

Hướng dẫn giải

\(\eqalign{
& a)\,\,\,S = {\rm{\{ }}x|x < 4\} \cr
& b)\,\,\,S = {\rm{\{ }}x|x \le - 2\} \cr
& c)\,\,\,S = {\rm{\{ }}x|x > - 3\} \cr
& d)\,\,S = {\rm{\{ }}x|x \ge 1\} \cr} \) 

Biểu diễn các tập nghiệm trên trục số: 

Câu 1: Biểu diễn tập nghiệm của bất phương trình sau trên trục số :

a) \(x > 5\)                                  b) \(x < -3\)

c) \(x ≥ 4\)                                  d) \(x ≤ -6\)

Câu 2: Cho tập \(A= \{-10, -9, -8, -7, -6, -5, -4, …,\) \( 8, 9, 10\}.\) Hãy cho biết giá trị nào của \(x\) trong tập \(A\) sẽ là nghiệm của bất phương trình :

a) \(\left| x \right| < 3\)                               b) \(\left| x \right|> 8\)

c) \(\left| x \right|≤ 4\)                               d) \(\left| x \right|≥ 7\)

Câu 3: Hãy đưa ra hai số nguyên là nghiệm của bất phương trình sau:

a) \( - 4x + 5 > 10\)

b) \(2x + 100 < 90\)

Câu 4: Viết thành bất phương trình và chỉ ra một nghiệm của nó từ các mệnh đề sau:

a) Tổng của một số nào đó và \(5\) lớn hơn \(7.\)

b) Hiệu của \(9\) và một số nào đó nhỏ hơn \(–12.\)

Câu 1: x=0,3 là nghiệm của bất phương trình:

A. 2x+5>7-0,3

B. 5x-1>0,4

C. 13(x+0,7)<4-(\(-\frac{1}{5}\))

D. \(\frac{1}{3}\)x+5

Câu 2: Chọn câu trả lời sai. x=-2,1 là nghiệm của bất phương trình 

A. 2(x-2,9)>5x-8

B. x-9 \(\geq\) x-13

C. 3x

D. x+5>3x

Câu 3: Cho bất phương trình -11x>5. Kết quả nào sau đây là đúng:

A. x=-1 là một nghiệm của bất phương trình 

B. x=1 là một nghiệm của bất phương trình 

C. x=-\(\frac{1}{2}\) là một nghiệm của bất phương trình 

D. x=0 không phải là nghiệm của bất phương trình 

Câu 4: Cho bất phương trình \(x^{2}

A. x=0 không phải là nghiệm của bất phương trình 

B. x=-1 là nghiệm của bất phương trình 

C. x=1 không phải là nghiệm của bất phương trình 

D. x=\(\frac{1}{2}\) là nghiệm của bất phương trình 

Câu 5: x=\(\frac{1}{3}\) là nghiệm của bất phương trình 

A. 12x<2-x

B. \(\frac{1}{3}\)x<-x

C. x+\(\frac{5}{7}\)>\(2\frac{1}{4}\)

D. 3x+5>6+x

Qua bài học này, các em nắm được một số nội dung chính như sau:

• Nắm được khái niệm bất phương trình một ẩn, tập nghiệm của bất phương trình
• Nắm được khái niệm bất phương trình tương đương