Toán 8 Chương 1 Bài 11: Hình thoi

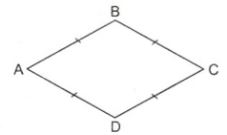
- Hình thoi là tứ giác có bốn cạnh bằng nhau.

Ví dụ: Hình thoi ABCD có bốn cạnh AB = BC = CD = AD.

- Từ định nghĩa này, ta suy ra: Hình thoi là hình bình hành có hai cạnh kề bằng nhau.

- Vì hình thoi cũng là hình bình hành nên hình thoi có tất cả tính chất của hình bình hành (chẳng hạn: Trong hình thoi hai đường chéo cắt nhau tại trung điểm của mỗi đường, các góc đối bằng nhau…)

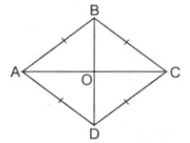
- Định lí:Trong hình thoi:

• Hai đường chéo vuông góc với nhau.
• Hai đường chéo là đường phân giác các góc của nó.

Ví dụ: ABCD là hình thoi \( \Rightarrow AB = BC = CD = DA\)

\(\begin{array}{l}AC \bot BD,OA = OC,OC = OB\\\widehat {{A_1}} = \widehat {{A_2}}.\end{array}\)

- Hình thoi có một tâm đối xứng là giao điểm của hai đường chéo.

- Hình thoi có hai trục đối xứng là hai đường chéo.

Để chứng minh một tứ giác là hình thoi, ta chứng minh nó có một trong các tính chất sau:

• Có bốn cạnh bằng nhau.
• Là hình bình hành có hai cạnh kề bằng nhau
• Là hình bình hành có hai đường chéo vuông góc với nhau.
• Là hình bình hành có một đường chéo là phân giác của một góc ở đỉnh.

Câu 1: Từ các đỉnh của một hình chữ nhật, ta kẻ các đường thẳng vuông góc với các đường chéo của hình chữ nhật. Chứng minh rằng các đường thẳng này cắt nhau tạo thành một hình thoi.

Hướng dẫn giải

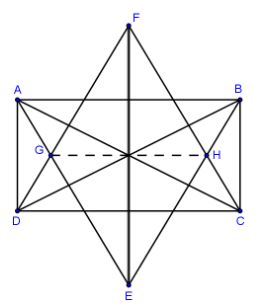
Dễ thấy FH // GE và GF//HE

\( \Rightarrow \) EHFG là hình bình hành (1)

\(\Delta AEB\) cân, \(\Delta CFD\) cân \( \Rightarrow \) F, E nằm trên trục đối xứng của hình chữ nhật. Tương tự, G, H nằm trên trục đối xứng thứ hai

\( \Rightarrow {\rm{EF}} \bot {\rm{GH}}\)    (2)

Từ (1) và (2) suy ra đpcm.

Câu 2: Cho hai đoạn thẳng MN và PQ bằng nhau và giao nhau tại trung điểm O của mỗi đoạn thẳng. Tại các đầu mút của mỗi đoạn thẳng, ta vẽ các đường thẳng vuông góc với đoạn thẳng ấy, các đường thẳng này cắt nhau theo thứ tự tại các điểm A, B, C,D.

a. Chứng minh rằng B và D đối xứng với nhau qua tâm O.

b. Chứng minh rằng B và D đối xứng với nhau qua trục AC.

c. Suy ra tứ giác ABCD là hình thoi.

Hướng dẫn giải

a. \(\Delta BMO = \Delta BQO \Rightarrow BM = BQ\)

Kết quả với \(BM \bot OM,BQ \bot OQ\)

Suy ra OB là tia phân giác của góc MOG

Tương tự, OD là tia phân giác của góc PON.

Hai góc MOQ và PON là hai góc đối đỉnh, vậy OB và OD là hai tia đối nhau, suy ra B, O, D thẳng hàng (1)

\(\Delta BMO = \Delta DNO \Rightarrow OB = OD\) (2)

Từ (1) và (2) suy ra B và D đối xứng với nhau qua tâm O.

b. Tương tự, ta chứng minh được OC là tia phân giác của góc QON và ba điểm A, O, C thẳng hàng OA = OC.

\(\widehat {MOQ}\) và \(\widehat {QON}\) là hai góc kề bù nên \(OB \bot OC\)  hay \(BD \bot AC\)

Kết hợp với OB = OD suy ra AC là trung trực của BD hay B và D đối xứng với nhau qua trục AC

c. BD là trung trực của đoạn thẳng AC.

AC là trung trực của đoạn thẳng BD

Vậy ABCD là hình thoi.

Câu 3: Cho hình thang cân ABCD. Gọi M, N, P, Q theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA.

a. Chứng minh MNPQ là hình thoi.

b. Chứng minh rằng một trong hai đường chéo của hình thopi MNPQ đi qua giao điểm của hai đường chéo của hình thang ABCD.

Hướng dẫn giải

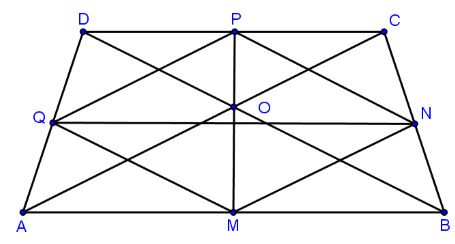
a. Ta có:

\(\begin{array}{l}PN = \frac{1}{2}DB;\,\,\,\,\,\,QM = \frac{1}{2}DB\\NM = \frac{1}{2}AC;\,\,\,\,\,PQ = \frac{1}{2}AC\end{array}\)

ABCD là  hình thang cân nên AC = BD.

Suy ra PN = MN = MQ = QP \( \Rightarrow \) MNPQ là hình thoi.

b. Gọi O là giao điểm của hai đường chéo AC, BD của hình thang.

Dễ dàng chứng minh được OA = OB; OC = OD \( \Rightarrow \) điểm O nằm trên đường trung trực của hai cạnh đáy hình thang ABCD \(O \in PM\) mà PM là một đường chéo của hình thoi MNPQ.

Câu 1: Trên các cạnh AB, BC, CD, DA của hình bình hành ABCD ta lấy các điểm E, M, N, F sao cho BM = DN và BE = DF. Gọi O, P, K, Q, R theo thứ tự là trung điểm của các đoạn thẳng BD, ED, BF, FE và MN.

a. Chứng minh OPQK là hình thoi

b. Chứng minh ba điểm Q, O, R thẳng hàng.

c. Trường hợp nào thì cả 5 điểm A, Q, O, R, C thẳng hàng.

Câu 2: Cho hình thoi ABCD. Trên tia đối của tia BA ta lấy điểm M; trên tia đối của tia CB lấy điểm N, trên tia đối của tia DC lấy điểm P và trên tia đối của tia AD lấy điểm Q sao cho BM = CN = DP = AQ.

a. Chứng minh tứ giác MNPQ là hình bình hành.

b. Chứng minh hình bình hành MNPQ và hình thoi ABCD có cùng một tâm đối xứng.

c. Hình thoi ABCD phải có điều kiện gì để MNPQ là hình vuông?

Câu 3: Giao điểm của hai đường chéo của hình bình hành ABCD là điểm O. Gọi M, N, P, Q theo thứ tự là các giao điểm của các đường phân giác trong của các tam giác OAB, OBC, OCD, ODA.

a. Chứng minh tứ giác MNPQ là hình thoi

b. Hình bình hành ABCD phải có điều kiện gì để MNPQ là hình vuông?

Câu 1: Chọn ý đúng

A. Hình thoi là tứ giác có các cạnh đối song song

B.  Hình thoi là tứ giác có ba góc vuông

C.  Hình thoi là tứ giác có bốn cạnh bằng nhau

D.  Hình thoi là tứ giác có 2 cạnh đối song song và bằng nhau

Câu 2:  Chọn ý sai

A.  Tứ giác có bốn cạnh bằng nhau là hình thoi

B.  Hình bình hành có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình thoi

C.  Hình bình hành có hai cạnh kề bằng nhau là hình thoi

D.  Hình bình hành có một đường chéo là đường phân giác của một góc là hình thoi

Câu 3: Cho hình thoi có hai đường chéo lần lượt là 6 cm và 8 cm, độ dài cạnh hình thoi nhận giá trị nào sau đây?

A. 2 cm

B. 7 cm

C. 12 cm

D.  5 cm

Câu 4:  Cạnh của một hình thoi có độ dài \(\sqrt {74} \)  thì độ dài hai đường chéo lần lượt là?

A. 10 cm;14 cm

B.  10cm; 12 cm

C. 14cm ; 16 cm

D. 12 cm; 16 cm

Câu 5:  Hình thoi có chu vi là 32 cm, cạnh hình thoi có giá trị là ?

A. 6 cm

B. 8 cm

C. 12 cm

D.  16 cm

Qua bài học này, các em cần nắm được những nội dung sau:

• Nhận biết được hình thoi.
• Ghi nhớ được tính chất của hình thoi.
• Vận dụng kiến thức giải được một số bài toán liên quan.