Toán 8 Chương 1 Bài 4: Đường trung bình của tam giác, của hình thang

- Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

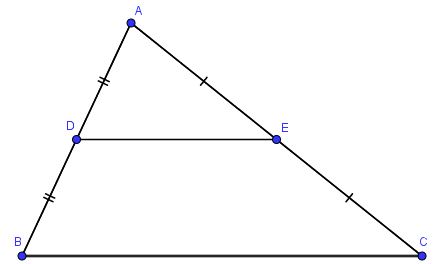
Ví dụ: Ở hình trên ta gọi DE là đường trung bình cùa tam giác ABC.

- Các định lí:

• Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

• Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

- Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm của hai cạnh bên của hình thang.

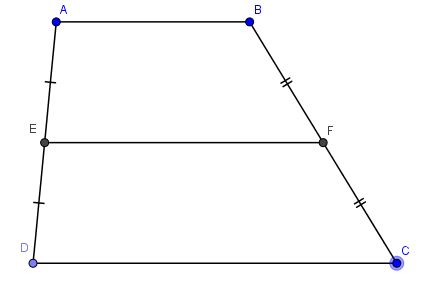
 Ví dụ: Ở hình trên ta gọi EF là đường trung bình của hình thang ABCD.

- Các định lí:

• Đường thẳng đi qua trung điểm một cạnh bên của hình thang và sông sông với hai đáy thì đi qua trung điểm cânhj bên thứ hai.

• Đường trung bình của hình thang thì song song với hai đáy và có độ dài bằng một nửa tổng hai đáy.

Câu 1: Cho tam giác ABC có D,E,F lần lượt là trung điểm của các danh AB,AC,BC. gọi G là trung điểm của AF. Chứng minh D,G,E thẳng hàng và G là trung điểm DE.

Hướng dẫn giải

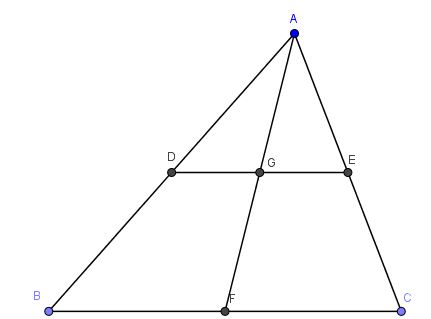
• Chứng minh D, G, E thẳng hàng

Xét tam giác ABF có:

D là trung điểm AB

G là trung điểm AF 

⇒DG là đường trung bình của tam giác ABF

\( \Rightarrow DG\parallel BF\) và \(DG = \frac{1}{2}BF\)

Xét tam giác AFC có:

G là trung điểm AF

E là trung điểm AC

⇒GE là đường trung bình của tam giác AFC

\( \Rightarrow GE\parallel FC\) và \(GE = \frac{1}{2}FC\)

Ta có: \( DG\parallel BF\) và \( GE\parallel FC\)  ⇒D, G, E thẳng hàng (tiên đề Euclid)

• Chứng minh G là trung điểm của DE

Ta có: \(DG = \frac{1}{2}BF\) và \(GE = \frac{1}{2}FC\)

Mà BF=CF (F là trung điểm BC)

⇒DG=GE

Mà D,E,G thẳng hàng

⇒G là trung điểm của DE

Câu 2: Cho tam giác ABC có BD và CE là các đường trung tuyến cắt nhau tại G, gọi I, K lần lượt theo hứ tự là trung điểm của GB và GC. Chứng minh rằng \(DE\parallel IK\) và DE=IK

Hướng dẫn giải

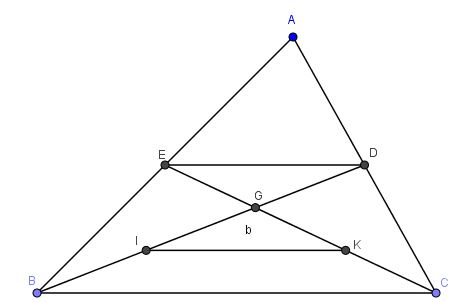
Xét tam giác ABC có:

E là trung điểm AB

D là trung điểm AC

⇒DE là đường trung bình của tam giác ABC.

\( \Rightarrow DE\parallel BC\) và \(DE = \frac{1}{2}BC\)

Tương tự với tam giác GBC ta cũng có:

I là trung điểm GB

K là trung điểm GC

⇒IK  là đường trung bình của tam giác GBC.

\( \Rightarrow IK\parallel BC\) và \(IK = \frac{1}{2}BC\)

\( \Rightarrow IK\parallel DE\) (cùng song song với BC ) và IK=DE (cùng bằng một nửa BC)

Câu 3: Cho hình thang ABCD có AB, CD là hai đáy va AB < CD. Gọi E và F lần lượt là trung điểm của BD và AC. Chứng minh rằng: \(EF = \frac{{CD - AB}}{2}\)

Hướng dẫn giải

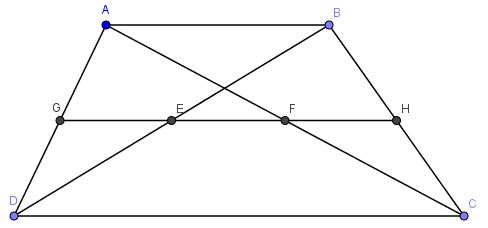
Gọi G và H lần lượt là trung điểm của AD và BC.

Xét tam giác ADC có:

G là trung điểm AD

F là trung điểm AC

⇒GF là đường trung bình của tam giác ADC

\( \Rightarrow GF\parallel DC\) và \(GF = \frac{1}{2}CD\)

Chứng minh tương tự với tam giác BCD ta cũng có: EH là đường trung bình của tam giác BCD

\( \Rightarrow EH\parallel CD\) và \(EH = \frac{1}{2}CD\)

Ta có \(GF\parallel DC\) và \(EH\parallel CD\) ⇒E,F,G,H thẳng hàng.

Xét tam giác ABD dễ thấy GE là đường trung bình của tam giác ABD nên \(GE = \frac{1}{2}AB\)

Tương tự với tam giác ABC ta cũng chứng minh được \(FH = \frac{1}{2}AB\)

Mặt khác ta có GH là đường trung bình của hình thang ABCD nên \(GH = \frac{{AB + CD}}{2}\)

Ta có

 \(\begin{array}{l} GH = GE + EF + FH\\ \,\,\,\,\,\,\,\, = \frac{1}{2}AB + EF + \frac{1}{2}AB\\ \,\,\,\,\,\,\,\,\,= AB + EF = \frac{{AB + CD}}{2} \end{array}\)

\( \Rightarrow EF = \frac{{CD - AB}}{2}\) (điều phải chứng minh)

Câu 1: Cho tam giác ABC, điểm D thuộc cạnh AC sao cho AD = 1/2 DC, Gọi M là trung điểm của BC, I là giao điểm của BD và AM. Chứng minh: AI = IM.

Câu 2: Hình thang ABCD có đáy AB, CD. Gọi E, F, I theo thứ tự là trung điểm của AD, BC, AC. Chứng minh rằng ba điểm E, F, I thắng hàng.

Câu 3: Cho tứ giác ABCD. Gọi E, F, I theo thứ tự là trung đếm của AD, BC, AC. Chứng minh rằng: EI//CD, IF//AB

Câu 4: Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6Cm, CD = l4cm. Tính độ dài MI, IK, KN.

Câu 1: Cho tam giác ABC có D là trung điểm AB, E là trung điểm AC, phát biểu nào sao đây sai?

A. DE là đường trung bình của tam giác ABC

B. DE song song với BC

C. DECB là hình thang cân

D. DE có độ dài bằng nửa BC

Câu 2: Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC và DE = 4 cm . Biết đường cao AH = 6 cm . Diện tích tam giác ABC bằng bao nhiêu?

A. \(S = 24c{m^2}\,\)

B. \(\,\,S = 12c{m^2}\,\,\)

C. \(S = 48c{m^2}\)

D. \(S = 32c{m^2}\)

Câu 3: Chọn phát biểu đúng

A. Đường trung bình của hình thang là đoạn thẳng nối các trung điểm của hai cạnh bên của hình thang

B. Đường trung bình của hình thang là đoạn thẳng nối các trung điểm của hai cạnh đối của hình thang

C. Đường trung bình của hình thang thì song song với hai đáy và bằng tổng hai đáy

D. Một hình thang có thể có một hoặc nhiều đường trung bình

Câu 4:   Với a,b, h lần lượt là đáy lớn, đáy nhỏ và chiều cao của hình thang thì công thức tính diện tích hình thang là?

A. \(S = \left( {a + b} \right).h\)

B. \(S = \frac{1}{2}\left( {a + b} \right).h\)

C. \(S = \frac{1}{3}\left( {a + b} \right).h\)

D. \(S = \frac{1}{4}\left( {a + b} \right).h\)

Qua bài học này, các em cần nắm được những nội dung sau:

• Xác định được đường trung bình của tam giác của hình thang.
• Ghi nhớ được các tính chất về đường trung bình của tam giác của hình thang.
• Vận dung kiến thức giải được các bài toán liên quan.