Toán 8 Chương 4 Bài 9: Thể tích của hình chóp đều
Với bài học này chúng ta tìm hiểu về thể tích của hình chóp và các dạng bài tập về tìm thể tích. Bài giảng này đã được eLib biên soạn các kiến thức và các dạng bài tập cụ thể chi tiết giúp các em dễ dàng nắm vững kiến thức. Sau đây mời các em cùng tham khảo.
Mục lục nội dung

1. Tóm tắt lý thuyết
Công thức tính thể tích:
Thể tích của hình chóp đều bằng một phần ba diện tích mặt đáy nhân với chiều cao
\(V = \dfrac{1}{3} .S.h\)
\(S\): diện tích đáy
\(h\): chiều cao
2. Bài tập minh họa
2.1. Bài tập 1
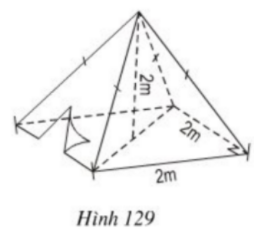
Hình 129 là một cái lều ở trại hè của học sinh kèm theo các kích thước.
a) Thể tích không khí bên trong lều là bao nhiêu?
b) Xác định số vải bạt cần thiết để dựng lều (không tính đến đường viền, nếp gấp, ... biết \(\sqrt{5} ≈ 2,24\)).
Hướng dẫn giải
a) Thể tích cần tính bằng thể tích của hình chóp có chiều cao \(2cm\), đáy là hình vuông cạnh dài \(2m\).
Diện tích đáy là: \( S_{đ} = 2.2=4(m^2)\)
Thể tích hình chóp là: \(V = \dfrac{1}{3}.S.h = \dfrac{1}{3}.4.2 = \dfrac{8}{3}\approx 2,67\)\(\,(m^3) \)
b) Số vải bạt cần tính chính là diện tích của bốn mặt (hay là diện tích xung quanh) mỗi mặt là một tam giác cân.
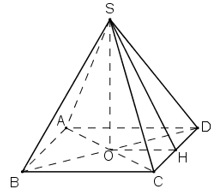
Gọi \(H\) là trung điểm của \(CD\) và \(O\) là tâm của hình vuông \(ABCD\).
Để tính diện tích xung quanh ta cần phải tính được trung đoạn tức là đường cao \(SH\) của mỗi mặt.
Theo định lý Pytago trong tam giác vuông SHA, ta có:
\(SH^2 =SO^2+OH^2 \)\(\,= SO^2+{\left( {\dfrac{{BC}}{2}} \right)^2} \) \(= 2^2+1^2=5\)
\( \Rightarrow SH =\sqrt{5}\approx 2,24(m) \)
Diện tích xung quanh của hình chóp là:
\( S_{xq} = p.d = \dfrac{1}{2}. 2.4.2,24 = 8,96 (m^2) \)
2.2. Bài tập 2
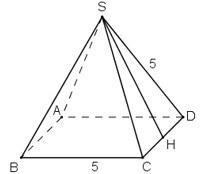
Tính diện tích toàn phần của hình chóp tứ giác đều, biết cạnh đáy \(a = 5cm\), cạnh bên \(b = 5cm,\;\sqrt{18,75}\approx 4,33 \)
Hướng dẫn giải
Từ đề bài ta có các mặt bên của hình chóp đều là những tam giác đều cạnh \(5cm\).
Đường cao của mỗi mặt bên là:
\(d=SH = \sqrt{SC^{2} -HC^{2}}\)
\(= \sqrt{5^{2} -2,5^{2}}= \sqrt{18,75}\approx 4,33 (cm) \)
Diện tích xung quanh hình chóp là:
\(S_{xq} = p.d = \dfrac{1}{2}. 5.4.4,33 = 43,3 (cm^2) \)
Diện tích đáy hình chóp: \(S_{đ} = a^2 = 5^2 =25(cm^2) \)
Diện tích toàn phần hình chóp:
\( S_{tp} = S_{xq}+ S_{đ} = 43,3 + 25 = 68,3 \) \((cm^2)\)
3. Luyện tập
3.1. Bài tập tự luận
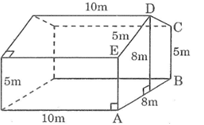
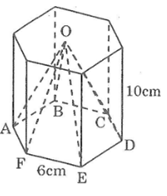
Câu 1: Một cái nhà trồng cây thí nghiệm có dạng hình lăng trụ đứng có các kích thước như hình vẽ trong đó EDC là tam giác cân.Hãy tính :
a) Diện tích hình ABCDE
b) Tính thể tích nhà kính
c) Diện tích kính cần phải có để “lợp” hai mái và bốn bức tường nhà
Câu 2: Kim tự tháp Kê-ốp (Thế kỉ 25 trước Công nguyên) là một hình chóp tứ giác đều, cạnh đáy bằng \(233m\), chiều cao hình chóp \(146,5m.\)
a) Độ dài cạnh bên là bao nhiêu?
b) Tính diện tích xung quanh của hình chóp.
c) Tính thể tích hình chóp.
Câu 3: Kim tự tháp Lu-vrơ (Louvre) (Xây dựng vào năm 1988).
Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-vrơ (Pháp). Mô hình có dạng chóp đều chiều cao \(21m,\) độ dài cạnh đáy là \(34m.\)
a) Cạnh bên của hình chóp là bao nhiêu?
b) Tính thể tích hình chóp.
c) Tính tổng diện tích các tấm kính để phủ lên hình chóp này \(({S_{xq}})\).
Câu 4: Thể tích hình chóp đều cho theo các kích thước ở hình là?
3.2. Bài tập trắc nghiệm
Câu 1: Thể tích hình chóp có đáy là tam giác đều có cạnh là 6, các cạnh bên bằng \(\sqrt{15}\) là:
A. 6
B. 9
C. \(\frac{27}{2}\)
D. \(\frac{9\sqrt{3}}{2}\)
Câu 2: Hình chóp tứ giác đều có độ dài cạnh bên là 5cm, chiều cao hình chóp là 4cm. Thể tích hình chóp là:
A. 30
B. 24
C. 22
D. 18
Câu 3: Một hình chóp tứ giác đều và một lăng trụ đứng tứ giác đều như hình vẽ dưới đây (cạnh đáy và chiều cao bằng nhau). Nếu thể tích hình chóp là V thì thể tích lăng trụ là:
A. V
B. 2V
C. 3V
D. 4V
Câu 4: Với mỗi đỉng của hình lập phương, ta xét hình chóp xác định bởi đỉnh ấy và các trung điểm của ba cạnh xuất phát từ đỉnh ấy.Khi ta cắt bỏ các hình chóp này thì tỉ số thể tích phần còn lại với thể tích khối lập phương ban đầu gần nhất với số nào dưới đây?
A. 75%
B. 68%
C. 81%
D. 84%
Câu 5: Một hình gồm hai hình chóp gắn liền được tạo thành bằng cách nối tâm cua rhia mặt liên tiếp của hình lập phương. vậy tỉ số thể tích được tạo đó và khối lập phương:
A. \(\frac{\sqrt{3}}{12}\)
B. \(\frac{\sqrt{6}}{16}\)
C. \(\frac{1}{6}\)
D. \(\frac{\sqrt{2}}{8}\)
4. Kết luận
Qua bài học này, các em nắm được một số nội dung chính như sau:
- Nắm được cách tính thể tích hình chóp đều.
- Biết áp dụng công thức tính toán đối với các hình cụ thể.
Tham khảo thêm
- doc Toán 8 Chương 4 Bài 1: Hình hộp chữ nhật
- doc Toán 8 Chương 4 Bài 2: Hình hộp chữ nhật (tiếp theo)
- doc Toán 8 Chương 4 Bài 3: Thể tích của hình hộp chữ nhật
- doc Toán 8 Chương 4 Bài 4: Hình lăng trụ đứng
- doc Toán 8 Chương 4 Bài 5: Diện tích xung quanh của hình lăng trụ đứng
- doc Toán 8 Chương 4 Bài 6: Thể tích của hình lăng trụ đứng
- doc Toán 8 Chương 4 Bài 7: Hình chóp đều và hình chóp cụt đều
- doc Toán 8 Chương 4 Bài 8: Diện tích xung quanh của hình chóp đều
- doc Toán 8 Ôn tập chương 4: Hình lăng trụ đứng. Hình chóp đều