Toán 8 Chương 1 Bài 10: Đường thẳng song song với một đường thẳng cho trước
Sau đây mời các em học sinh lớp 8 cùng tìm hiểu về bài Đường thẳng song song với một đường thẳng cho trước. Bài giảng dưới đây đã được eLib biên soạn khái quát lý thuyết cần nhớ, đồng thời có các bài tập được tổng hợp đầy đủ các dạng toán liên quan giúp các em dễ dàng nắm được kiến thức trọng tâm của bài.
Mục lục nội dung

1. Tóm tắt lý thuyết
1.1. Khoảng cách giữa hai đường thẳng song song:
- Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thằng này đến đường thẳng kia.
1.2. Tính chất của các điểm các đều một đường thẳng cho trước:
- Tính chất: Các điểm cách đều một đường thẳng b một khoảng là h nằm trên hai đường thẳng song song với b và cách b một khoảng là h.
- Nhận xét: Tập hớp các điểm cách đều một đường thẳng cố định một khoảng không đổi h là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.
1.3. Đường thẳng song song cách đều:
- Cho các đường thẳng a,b,c,d song song với nhau và khoẳng cách giữa các đường thẳng a và b, b và c, c và d bằng nhau. Khi đó ta gọi a,b,c,d là các đường thẳng song song cách đều.

- Bên cạnh đó từ việc sử dụng các kiến thức đã học về hình chữ nhật, tam giác bằng nhau và các góc tạo bởi hai đường song song và cát tuyến. Ta có thể dễ dàng chứng minh được các hệ quả sau:
- Nếu các đường thẳng song song cách đều cắt một đường thẳng thì chúng chắn trên đường thẳng đó các đoạn thẳng iên tiếp bằng nhau.
- Nếu các đường thẳng song song cắt một đường thẳng và chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau thì chúng song song cách đều.
2. Bài tập minh họa
Câu 1: cho tam giác ABC có trọng tâm G, E là trung điểm của AG, các đường thẳng song song với BC và qua E và G lần lượt cắt AB tại các điểm F và H. Chứng minh rằng \(AF=FH=HB\).
Hướng dẫn giải
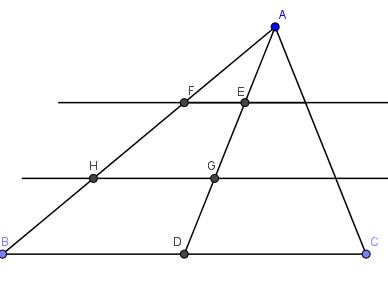
Gọi D là trung điểm của BC, ta có AG=2DG (do G là trọng tâm tam giá ABC)
Ta có AG=2AE =2EG (do E là trung điểm AG)
⇒AE=EG=DG
Xét tam giác AHG có:
E là trung điểm AG
EF song song HG
⇒F là trung điểm của AH
⇒AF=FH(1)
Mặt khác ta lại có các đường thẳng EF, HG, BC song song với nhau.
mà EG=GD nên EF, HG, BC là các đường thẳng song song cách đều.
nên FH=HB(2)
Từ (1) và (2) ta có: AF=FH=HB.
Câu 2: Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy. Vẽ về một phía của AB các tam giac đều AMD, BME. Trung điểm I của DE di chuyển trên đường nào.
Hướng dẫn giải
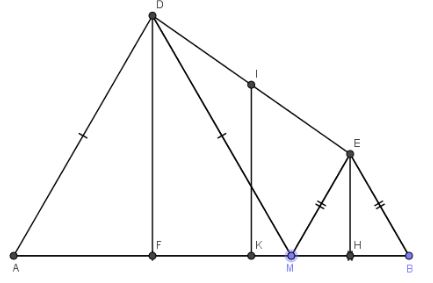
Gọi F, K, H lần lượt là hình chiếu của D,I,E lên AB.
Dễ thấy DEHF là hình thang với hai đáy là EH và DF
Ta lại có I trung điểm của DE và \(IK\parallel EH\parallel DF\) nên IK là đường trung bình của hình thang DEHF.
\( \Rightarrow IK = \frac{{EH + DF}}{2}\)
Xét tam giác ADF vuông tại F có:
\(\begin{array}{l} A{F^2} + D{F^2} = A{D^2}\\ \Rightarrow D{F^2} = A{D^2} - A{F^2}\\ \end{array}\)
Mặt khác AD=AM (tam giác ADM đều); \(AF = \frac{1}{2}AM\) (F trung điểm AM vìa tam giác ADM đều và AF là đường cao)
Ta được:
\(\begin{array}{l} D{F^2} = A{D^2} - A{F^2} = A{M^2} - {\left( {\frac{1}{2}AM} \right)^2} = A{M^2} - \frac{1}{4}A{M^2} = \frac{3}{4}A{M^2}\\ \Rightarrow DF = \frac{{\sqrt 3 }}{2}AM \end{array}\)
Tương tự cho tam giác vuông EHB ta cũng chứng minh được \(EH = \frac{{\sqrt 3 }}{2}MB\)
Ta có:
\(IK = \frac{{EH + DF}}{2} = \frac{{\frac{{\sqrt 3 }}{2}MB + \frac{{\sqrt 3 }}{2}AM}}{2} = \frac{{\sqrt 3 }}{4}\left( {MB + AM} \right) = \frac{{\sqrt 3 }}{4}AB\) (vì AB cố định nên IK khôn đổi)
Vậy khi M di chuyển thì I nằm trên đường thẳng song song với AB và cách AB một khoảng là \(\frac{{\sqrt 3 }}{4}AB\) và cùng phía với DE
Câu 3: Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh BC, gọi E,D lần lượt là chân các đường vuông góc kẻ từ M đến AB,AC. TÌm vị trí của M trên BC sao cho độ dài DE là nhỏ nhất
Hướng dẫn giải
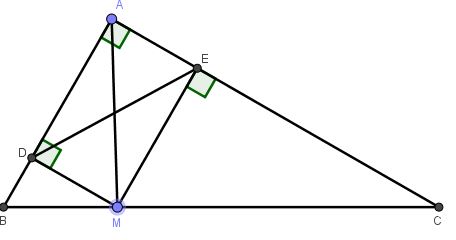
Dễ thấy rằng tứ giác ADME có 3 góc vuông nên là hình chữ nhật ⇒ AM=DE
nên vị trí điểm M sao cho DE nhỏ nhất tức là vị trí điểm M sao cho AM nhỏ nhất
mà AM nhỏ nhất chỉ khi M là hình chiếu của A lên BC
Vây DE nhỏ nhất khi M là hình chiếu của A lên BC hay AM vuông góc với BC
3. Luyện tập
3.1. Bài tập tự luận
Câu 1: Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tian Ax lấy điểm C, D, E sao cho AC=CD=DE. Kẻ đoạn thẳng EB. Quan C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.
Câu 2. Cho điểm A nằm ngoài đường thẳng d và có khoảng cách đến d bằng 2cm lấy điểm B bất kì thuộc đường thằng d. Gọi C là điểm đối xứng với điểm A qua điểm B. Khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường nào?
Câu 3: Cho tam giác ABC vuông tại A. Lấy M là một điểm bất kì thuộc cạnh BC. Gọi MD là đường vuông góc kẻ từ M đến AB, ME là đường vuông góc kẻ từ M đến AC, O là trung điểm của DE.
a) Chứng mình rằng ba điểm A, O, M thằng hàng.
b) Khi điểm M di chuyển trên cạnh BC thì điểm O di chuyển trên đường nào?
3.2. Bài tập trắc nghiệm
Câu 1: Cho tam giác ABC, trên cạnh BC lấy điểm M. Gọi I là trung điểm của AM, Khi M di chuyển trên BC thì I di chuyển trên?
A. Điểm I di chuyển trên đường trung trực của BC
B. Một đường thẳng bất kỳ không xác định
C. Đường trung bình của đoạn thẳng BC
D. Đường trung bình của tam giác ABC
Câu 2: Phát biểu nào dưới đây là đúng?
A. Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến đường thẳng kia.
B. Khoảng cách giữa hai đường thẳng song song là khoảng cách từ một điểm tùy ý trên đường thẳng này đến một điểm tùy ý trên đường thẳng kia.
C. Khoảng cách giữa hai đường thẳng song song là độ dài từ một điểm tùy ý trên đường thẳng này đến một điểm tùy ý trên đường thẳng kia.
D. Khoảng cách giữa hai đường thẳng song song là độ dài từ một điểm bất kỳ ở ngoài hai đường thẳng đến hai đường thẳng đó.
Câu 3: Các điểm cách đường thẳng a một khoảng 5cm thì
A. Nằm trên một đường thẳng song song với đường thẳng với a
B. Nằm trên hai đường thẳng song song với đường thẳng với a và cách a một khoảng bằng 5cm
C. Nằm trên một đường thẳng song song với đường thẳng với a và cách a một khoảng bằng 5cm
D. Nằm trên một đường thẳng cách a một khoảng bằng 5cm
Câu 4: Cho a và b là hai đường thẳng song song và có khoảng cách bằng 3 cm, A là điểm thuộc đường thẳng a, phát biểu nào sau đây đúng?
A. Khoảng cách từ điểm A đến một điểm bất kỳ thuộc b bằng 3cm
B. Khoảng cách từ điểm A đến một điểm bất kỳ thuộc a bằng 3cm
C. Khoảng cách từ điểm A đến b bằng 3 cm
D. A song song với b
Câu 5: Nếu các đường thẳng song song cách đều cắt một đường thẳng thì
A. Chúng song song cách đều với đường thẳng đó
B. Chúng cách đều đường thẳng đó
C. Chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp song song nhau
D. Chúng chắn trên đường thẳng đó các đoạn thẳng liên tiếp bằng nhau
4. Kết luận
Qua bài học này, các em cần nắm được những nội dung sau:
- Xác đinh được khoảng cách giữa hai đường thẳng song song cho trước.
- Ghi nhớ được tính chất của các điểm cách đều một đường thẳng cho trước, tính chất của các đường thẳng song song cách đều.
- Vận dụng kiến thức để giải các bài toán liên quan.
Tham khảo thêm
- doc Toán 8 Chương 1 Bài 1: Tứ giác
- doc Toán 8 Chương 1 Bài 2: Hình thang
- doc Toán 8 Chương 1 Bài 3: Hình thang cân
- doc Toán 8 Chương 1 Bài 4: Đường trung bình của tam giác, của hình thang
- doc Toán 8 Chương 1 Bài 5: Dựng hình bằng thước và compa và Dựng hình thang
- doc Toán 8 Chương 1 Bài 6: Đối xứng trục
- doc Toán 8 Chương 1 Bài 7: Hình bình hành
- doc Toán 8 Chương 1 Bài 8: Đối xứng tâm
- doc Toán 8 Chương 1 Bài 9: Hình chữ nhật
- doc Toán 8 Chương 1 Bài 11: Hình thoi
- doc Toán 8 Chương 1 Bài 12: Hình vuông
