Giải bài tập SGK Vật lý 10 Nâng cao Bài 13: Lực. Tổng hợp và phân tích lực

Gọi F₁; F₂ là độ lớn của hai lực thành phần, F là độ lớn hợp lực của chúng. Câu nào sau đây là đúng ?

A. Trong mọi trường hợp F luôn luôn lớn hơn cả F₁ và F₂

B. F không bao giờ nhỏ hơn cả F₁ và F₂

C. Trong mọi trường hợp, F thõa mãn: \(\left| {{F_1} - {F_2}} \right| \le F \le {F_1} + {F_2}\)

D. F không bao giờ bằng F₁ hoặc F₂

Phương pháp giải

Áp dụng quy tắc hình bình hành để tính độ lớn của hợp lực F

Hướng dẫn giải

- Ta có: \(\vec F = {\mkern 1mu} {\mkern 1mu} \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)

\(F = \sqrt {F_1^2 + F_1^2 + 2{F_1}{F_2}\cos \alpha } \)

Vì 0^o ≤ α ≤ 180^o nên -1 ≤ cosα ≤ 1 ⇒ |F₁ - F₂| ≤ F ≤ |F₁ + F₂|.

Cho hai lực đồng quy có độ lớn: F₁=F₂=20N

Hãy tìm độ lớn hợp lực của hai lực khi chúng hợp lực với nhau một góc α=0⁰,60⁰,90⁰,120⁰,180⁰.

Vẽ hình biểu diễn cho mỗi trường hợp. 

Nhận xét về ảnh hưởng của góc α đối với độ lớn của hợp lực

Phương pháp giải

Áp dụng công thức:

\(F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos \alpha } \) để tính F với mỗi góc α tương ứng

Hướng dẫn giải

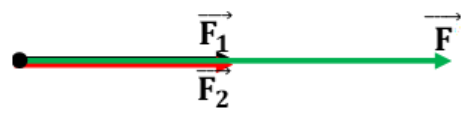
a) α=0⁰

F=F₁+F₂=40N

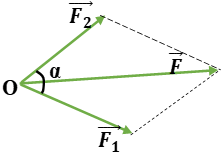
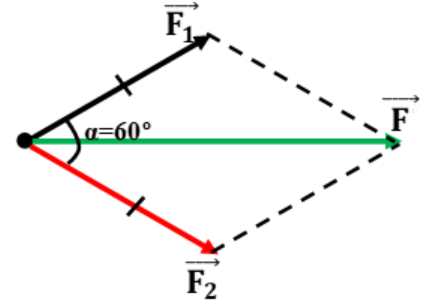
b) α=60⁰

\(\begin{array}{l} F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos {{60}^0}} \\ \Rightarrow F = 2.{F_2}.\cos \frac{\alpha }{2} = 2.20.\frac{{\sqrt 3 }}{2} = 20\sqrt 3 {\mkern 1mu} N \end{array}\)

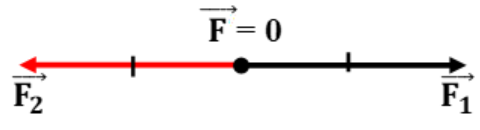
c) α=180⁰

F=0N

d) α=90⁰

\(\begin{array}{l} F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos {{90}^0}} \\ \Rightarrow F = {F_1}\sqrt 2 = 20\sqrt 2 {\mkern 1mu} (N) \end{array}\)

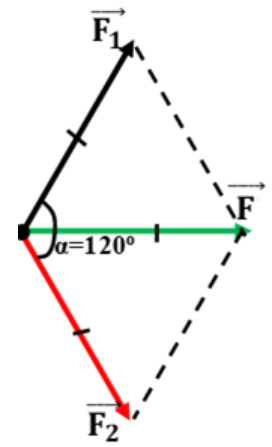
e) α=120⁰

\(\begin{array}{l} F = \sqrt {F_1^2 + F_2^2 + 2{F_1}{F_2}.\cos {{120}^0}} \\ \Rightarrow F = {F_1} = {F_2} = 20{\mkern 1mu} N \end{array}\)

Cho hai lực đồng quy có độ lớn F₁=16N và F₂=12N

a) Hợp lực của chúng có thể có độ lớn 30N hoặc 3,5N được không ?

b) Cho biết độ lớn của hợp lực F = 20 N. Hãy tìm góc giữa lực  \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \)

Phương pháp giải

a) Dựa vào giới hạn giá trị của tổng hợp lực để trả lời câu hỏi này

b) Độ lớn của hai lực thành phần thỏa:

F²=F₁²+F₂² ⇒ vecto của hai lực vuông góc nhau

Hướng dẫn giải

F₁=16N; F₂=12N

a) Ta có: |F₁−F₂| ≤ F ≤ F₁+F₂

Hợp lực \(\overrightarrow {{F_1}} \) có độ lớn 4 ≤ F ≤ 28 (N) do đó F không thể lấy giá trị 30 (N) hoặc 3,5 (N) được.

b) Góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là:

 \(\begin{array}{l} \vec F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \\ F = 20{\mkern 1mu} N{\mkern 1mu} ;{\mkern 1mu} {F_1} = 16N{\mkern 1mu} ;{F_2} = 12{\mkern 1mu} N \end{array}\)

=>F²=F₁²+F₂² tam giác lực là tam giác vuông với \(\overrightarrow {{F_1}} \bot \overrightarrow {{F_2}} \)

Vậy góc \(\alpha = (\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ) = {90^0}.\)

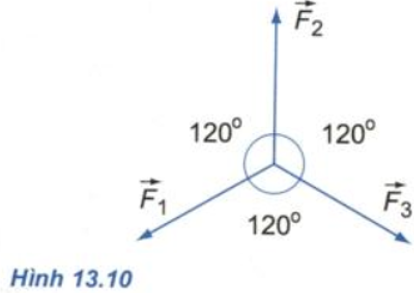
Cho ba lực đồng quy cùng nằm trong một mặt phẳng, có độ lớn bằng nhau và từng đôi một làm thành góc 120^o (hình 13.10). Tìm hợp lực của chúng.

Phương pháp giải

- Áp dụng quy tắc hình bình hành vẽ hình tổng hợp lực

- Hợp lực được tính theo công thức:

\(\overrightarrow {F{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} } = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} {\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} \overrightarrow {F'{\mkern 1mu} } + {\vec F_3} = \vec 0\)

Hướng dẫn giải

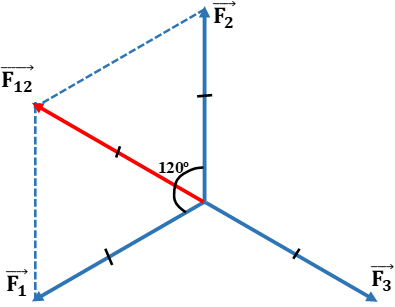
Ta có: 

\(\overrightarrow {F{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} } = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} {\mkern 1mu} {\mkern 1mu} = {\mkern 1mu} \overrightarrow {F'{\mkern 1mu} } + {\vec F_3} \)

Hình bình hành OF₁F’F₂ là hình thoi gồm hai tam giác đều

nên F’ = F₁ = F₂ = F₃ và α=60⁰

\(\overrightarrow {F'} \)nằm trong mặt phẳng chứa \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} \)

\(\begin{array}{l} = > {\mkern 1mu} \overrightarrow {F'} {\mkern 1mu} {\rm{\; và \;}}{\mkern 1mu} \overrightarrow {{F_3}} trực đối \\ = > \vec F = \overrightarrow {F'} + \overrightarrow {{F_3}} = \vec 0 \end{array}\)

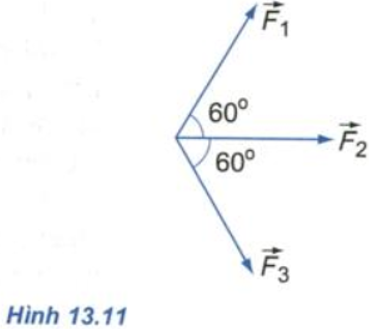
Hãy dùng quy tắc hình bình hành và quy tắc đa giác để tìm hợp lực của ba lực \(\overrightarrow {{F_1}} \),\(\overrightarrow {{F_2}} \) và \(\overrightarrow {{F_3}} \) có độ lớn bằng nhau và nằm trong cùng một mặt phẳng. Biết rằng lực \(\overrightarrow {{F_2}} \) làm thành với hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_3}} \) những góc đều là 60⁰ (Hình 13.11).

Phương pháp giải

- Áp dụng quy tắc hình bình hành vẽ hình tổng hợp lực

- Hợp lực được tính theo công thức:

\(\begin{array}{l} \vec F = \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_1}} = \overrightarrow {{F_2}} + \overrightarrow {F'} = 2\overrightarrow {{F_2}} \\ \end{array}\)

Hướng dẫn giải

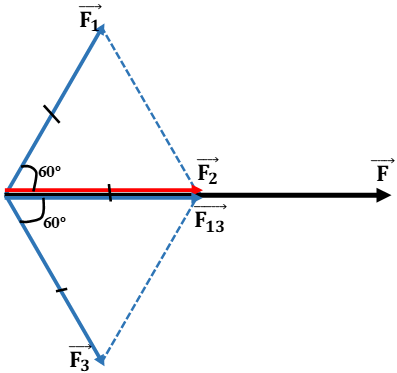
Ta có: 

\(\begin{array}{l} \vec F = \overrightarrow {{F_2}} + \overrightarrow {{F_3}} + \overrightarrow {{F_1}} = \overrightarrow {{F_2}} + \overrightarrow {F'} = 2\overrightarrow {{F_2}} \\ \overrightarrow {F'} = \overrightarrow {{F_2}} \to \vec F = 2\overrightarrow {{F_2}} \end{array}\)

Vậy \({\vec F}\) có độ lớn F=2F₂ có cùng phương, cùng chiều với \(\overrightarrow {{F_2}} \)

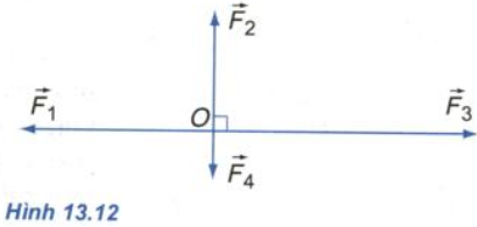
Tìm hợp lực của bốn lực đồng quy trong Hình 13.12.

Biết F₁=5N, F₂=3N, F₃=7N, F₄=1N

Phương pháp giải

- Tổng hợp lực F theo hai thành phần:

\(\vec F = \overrightarrow {F'} + \overrightarrow {F''} \)

- Áp dụng quy tắc hình bình hành để tổng hợp lực F':

\(\overrightarrow {F'} = \overrightarrow {{F_1}} + \overrightarrow {{F_3}} \)

- Áp dụng quy tắc hình bình hành để tổng hợp lực F'':

\(\overrightarrow {F''} = \overrightarrow {{F_2}} + \overrightarrow {{F_4}} \)

- Dựa vào hình vẽ xác định chiều của các lực F

Hướng dẫn giải

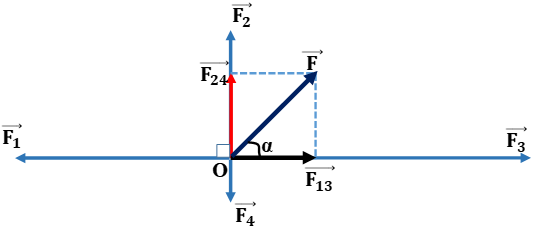
\(\overrightarrow {F'} = \overrightarrow {{F_1}} + \overrightarrow {{F_3}} \) có:

+ độ lớn F′=F₃−F₁=7−5=2N 

+ chiều của \(\overrightarrow {{F_3}} \)

\(\overrightarrow {F''} = \overrightarrow {{F_2}} + \overrightarrow {{F_4}} \) có:

+ độ lớn F′′=F₂−F₄=3−1=2N 

+ chiều của \(\overrightarrow {{F_2}} \)

 Hợp lực \(\vec F = \overrightarrow {F'} + \overrightarrow {F''} \) có:

+ độ lớn F=2√2N

+ hướng hợp với \(\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} \) cùng một góc α=45⁰

Một chiếc mắc áo treo vào điểm chính giữa của dây thép AB. Khối lượng tổng cộng của mắc áo và áo là 3 kg (Hình 13.13).

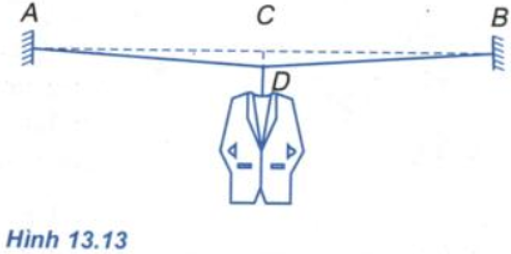
Biết AB = 4m; CD =10 cm

Tính lực kéo mỗi nửa sợi dây.       

Phương pháp giải

- Áp dụng quy tắc hình bình hành để vẽ hình phân tích lực đối với chiếc mắc áo treo

- Tính lực căng dây theo công thức:

\({T_1} = {T_2} = {F_1} = {F_2} \) với \(\begin{array}{l} {F_1} = {F_2} = \frac{{mg\sqrt {A{C^2} + C{D^2}} }}{{2CD}}\\ \end{array}\)

Hướng dẫn giải

∆DAB cân tại D có đường trung trực DC trùng với giá của trọng lực \(\vec P\) tác dụng lên mắc và áo nên nếu phân tích \(\vec P = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} \) như hình vẽ thì hình bình hành là hình thoi và \({F_1} = {F_2} = \frac{{DI}}{{\sin \alpha }}{\mkern 1mu} ;\) với \(DI = \frac{P}{2} = \frac{{mg}}{2};\sin \alpha = \frac{{CD}}{{AD}} = \frac{{CD}}{{\sqrt {A{C^2} + C{D^2}} }}\)

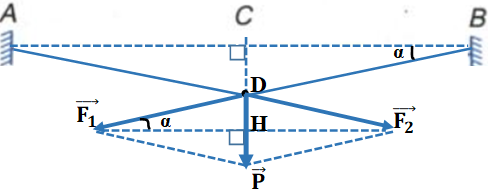
Ta được: 

\(\begin{array}{l} {F_1} = {F_2} = \frac{{mg\sqrt {A{C^2} + C{D^2}} }}{{2CD}}\\ = \frac{{3.9,8\sqrt {{2^2} + {{0,1}^2}} }}{{2.0,1}} \approx 294,4(N) \end{array}\)

Chất điểm D cân bằng dưới tác dụng của 4 lực đôi một cùng phương ngược chiều và F₁=F₂ nên \({T_1} = {T_2} = {F_1} = {F_2} = 294,4{\mkern 1mu} N\)

Vậy lực căng mỗi nhánh dây là 294,4 N.