Giải bài tập SGK Vật lý 10 Nâng cao Bài 56: Sự hóa hơi và sự ngưng tụ

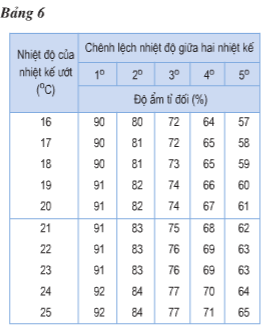
Dùng ẩm kế khô-ướt để đo độ ẩm tỉ đối của không khí. Nhiệt kế khô chỉ 24℃, hiệu nhiệt độ giữa hai nhiệt kế là 4℃. Độ ẩm tỉ đối của không khí là bao nhiêu?

A. 77%

B. 70%

C. 67%

D. 61% 

Phương pháp giải

Dựa vào số liệu bảng 6 trang 278 SGK về độ ẩm tỉ đối của không khí để trả lời câu hỏi này

Hướng dẫn giải

- Khi nhiệt kế khô chỉ 24℃ thì nhiệt kế ướt chỉ 20℃ và hiệu nhiệt độ giữa hai nhiệt kế là 4℃

- Tra bảng 6 trang 278 SGK ta thấy độ ẩm tỉ đối là 67%

- Chọn đáp án C.

Không gian trong xilanh ở bên dưới pittong có thể tích V₀ = 5,0 l chứa hơi nước bão hòa ở nhiệt độ t = 100^oC. Nén hơi đẳng nhiệt đến thể tích V = 1,6 l. Tìm khối lượng nước ngưng tụ (có thể áp dụng phương trình Cla-pê-rôn-Men-đê-lê-ép cho hơi bão hòa). 

Phương pháp giải

Áp dụng phương trình Cla-pê-rôn-Men-đê-lê-ép để tìm khối lượng nước ngưng tụ theo công thức:

\(\begin{array}{l} m = \frac{{p{\rm{\Delta }}V\mu }}{{RT}}\\ \end{array}\)với \({\rm{\Delta }}V = {V_0} - V\)

Hướng dẫn giải

Ta có:

\(\begin{array}{l} t = {100^ \circ }C = const\\ {p_b} = 760mmHg = 1,{013.10^5}Pa \end{array}\)

Khí nén đẳng nhiệt áp suất hơi tăng vượt áp suất hơi bão hòa nên hơi ngưng tụ cho tới khi lại có áp suất \({p_b} = 760\) mmHg

- Lượng hơi nước đã ngưng tụ là:

\({\rm{\Delta }}V = {V_0} - V = 5 - 1,6 = 3,4(l)\)

- Áp dụng phương trình Cla-pê-rôn-Men-đê-lê-ép cho hơi bão hòa, ta có:

\(\begin{array}{l} p{\rm{\Delta }}V = \frac{m}{\mu }RT\\ \Rightarrow m = \frac{{p{\rm{\Delta }}V\mu }}{{RT}}\\ \Rightarrow m = \frac{{1,{{013.10}^5}.3,{{4.10}^{ - 3}}.18}}{{8,31.373}} \approx 2(g) \end{array}\)

Để xác định nhiệt hóa hơi của nước, người ta làm thí nghiệm sau: Đưa 10g hơi nước ở nhiệt độ 100^oC vào một nhiệt lượng kế chứa 290g nước ở 20^oC. Nhiệt độ cuối của hệ là 40^oC. Hãy tính nhiệt hóa hơi của nước, cho biết nhiệt dung của nhiệt lượng kế là 46 J/độ, nhiệt dung riêng của nước là 4,18 J/g.độ 

Phương pháp giải

Để tìm nhiệt hóa hơi của nước ta làm như sau:

- Tìm nhiệt lượng tỏa ra theo công thức: 

Q_tỏa = Q₁ + Q₂ = m₁.L + m₁.C.(t₁ – t)

- Tìm nhiệt lượng thu vào theo công thức:

\(\begin{array}{l} {Q_{thu}} = Q_1^\prime + Q_2^\prime \\ = ({m_2}c + C').(t - {t_2})\\ \end{array}\)

- Áp dụng phương trình cân bằng nhiệt:

Q_thu = Q_tỏa để tìm nhiệt hóa hơi L

Hướng dẫn giải

Nhiệt lượng tỏa ra gồm hai phần: Nhiệt hóa hơi của 10g hơi nước và nhiệt tỏa ra khi 10g nước nguội từ 100^oC tới 40^oC:

Q_tỏa = Q₁ + Q₂ = m₁.L + m₁.C.(t₁ – t)

= 0,01.L + 0,01.4180.(100 – 40)

= 0,01.L + 2508 (J)

- Nhiệt lượng thu cũng gồm 2 phần:

+ Nhiệt lượng thu vào để 290g nước 20^oC nóng lên 40^oC.

+ Nhiệt lượng thu vào để nhiệt lượng kế 20^oC nóng lên 40^oC.

\(\begin{array}{l} {Q_{thu}} = Q_1^\prime + Q_2^\prime \\ = ({m_2}c + C').(t - {t_2})\\ = (0,290.4180 + 46).(40 - 20)\\ \Rightarrow {Q_{thu}} = 25164(J) \end{array}\)

- Ta có phương trình cân bằng nhiệt: Q_thu = Q_tỏa

⇔ 25164 = 0,01.L + 2508

\(\begin{array}{l} \Rightarrow L = \frac{{25164 - 2508}}{{0,01}} = 2265600(J)\\ \Rightarrow L \approx 2,27.106J \end{array}\)

Nhiệt độ của không khí là 30^oC. Độ ẩm tỉ đối là 64%. Hãy xác định độ ẩm tuyệt đối và độ sương.

Ghi chú: Tính các độ ẩm theo áp suất riêng phần. 

Phương pháp giải

- Áp dụng công thức: a=f.A để tính độ sương

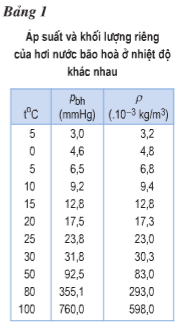
- Dựa vào tính chất độ: tăng Δa tỉ lệ thuận với độ tăng Δt, kết hợp với số liệu bảng 1 để tìm độ sương t_s

Hướng dẫn giải

Theo bảng 1 ( trang 273 SGK), áp suất riêng phần của hơi nước bão hòa ở 30^oC$$ là 31,8 mmHg nên A=31,8 mmHg.

- Độ ẩm tuyệt đối là:

\(\begin{array}{l} f = \frac{a}{A}\\ \Rightarrow a = fA = 64{\rm{\% }}.31,8 = 20,4(mmHg) \end{array}\)

- Muốn tìm \({t_s}\)  (điểm sương), ta phải dựa vào độ ẩm tuyệt đối \(a = 20,4\:mmHg\)

Tra bảng 1 (trang 273), ta thấy nhiệt độ \({20^ \circ }C < {t_S} < {25^ \circ }C\)

- Coi độ tăng Δa tỉ lệ thuận với độ tăng của nhiệt độ thì ta có:

\(\begin{array}{*{20}{c}} {}&{\frac{{{t_S} - 20}}{{20,4 - 17,5}} = \frac{{25 - {t_S}}}{{23,8 - 20}}}\\ {}&{ \Rightarrow {t_S} = 22,3{(^ \circ }C)} \end{array}\)