Giải bài tập SGK Vật lý 10 Nâng cao Bài 32: Chuyển động bằng phản lực. Bài tập về định luật bảo toàn động lượng

Hai xe lăn nhỏ có khối lượng m1=300g và m2 = 2kg chuyển động trên mặt phẳng ngang ngược chiều nhau với các vận tốc tương ứng v₁=2m/s và v₂=0,8m/s. Sau khi va chạm, hai xe dính vào nhau và chuyển động với cùng vận tốc. Tìm độ lớn và chiều của vận tốc này. Bỏ qua mọi lực cản.

Phương pháp giải

Dựa vào định luật bảo toàn động lượng, độ lớn của vận tốc ban đầu của xe được tính theo công thức:

\(v = \frac{{{m_1}{v_1} - {m_2}{v_2}}}{{{m_1} + {m_2}}}\)

Hướng dẫn giải

Mặt phẳng ngang, không ma sát nên hệ hai xe lăn là kín.

- Áp dụng định luật bảo toàn động lượng:

\(\begin{array}{l} ({m_1} + {m_2})\vec v = {m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} \\ \Rightarrow \vec v = \frac{{{m_1}\overrightarrow {{v_1}} + {m_2}\overrightarrow {{v_2}} }}{{{m_1} + {m_2}}}(1) \end{array}\)

- Chọn chiều dương là chiều chuyển động ban đầu của xe 1 thì (1)

⇒ \(v = \frac{{{m_1}{v_1} - {m_2}{v_2}}}{{{m_1} + {m_2}}} = \frac{{0,3.2 - 2.0,8}}{{0,3 + 2}} \approx - 0,43(m/s)\)

Sau va chạm 2 xe chuyển động cùng chiều xe 2 (trước va chạm) với tốc độ 0,43(m/s).

Một tên lửa có khối lượng tổng cộng M = 10 t đang bay với vận tốc V=200m/s đối với Trái Đất thì phụt ra phía sau (tức thời) khối lượng khí m=2t với vận tốc v=500m/s đối với tên lửa . Tìm vận tốc tức thời của tên lửa sau khi phụt khí với giả thiết toàn bộ khối lượng khí được phụt ra cùng một lúc.

Phương pháp giải

- Áp dụng định luật bảo toàn động lượng:

\(M\vec V = (M - m)\overrightarrow {V'} + m\vec v\)

- Chiếu lên phương chuyển động, tìm được vận tốc của tên lửa theo công thức:

\(V' = V - \frac{m}{{M - m}}( - {v_0}) = V + \frac{m}{{M - m}}{v_0}\)

Hướng dẫn giải

- Vận tốc của khí đối với Trái Đất:

\(\vec v = \overrightarrow {{v_0}} + \vec V\)

\(\vec v_o\) là vận tốc của khí đối với đất: v₀=500m/s.

\(\vec V\) là vận tốc của tên lửa đối với đất trước khi phụt khí.

- Gọi \(\vec V'\) là vận tốc của tên lửa đối với đất sau khi phụt khí.

- Coi hệ “ tên lửa” là kín trong thời gian phụt khí, áp dụng định luật bảo toàn động lượng:

\(\begin{array}{l} M\vec V = (M - m)\overrightarrow {V'} + m\vec v\\ = (M - m)\overrightarrow {V'} + m(\overrightarrow {{v_0}} + \vec V)\\ \overrightarrow {V'} = \frac{{(M - m)\vec V - m\overrightarrow {{v_0}} }}{{M - m}} = \vec V - \frac{m}{{M - m}}\overrightarrow {{v_0}} (1) \end{array}\)

- Chọn chiều dương là chiều chuyển động ban đầu của tên lửa thì (1)

\(\begin{array}{l} \Rightarrow V' = V - \frac{m}{{M - m}}( - {v_0}) = V + \frac{m}{{M - m}}{v_0}\\ V' = 200 + \frac{2}{{10 - 2}}.500 = 325(m/s) \end{array}\)

Tên lửa chuyển động theo hướng cũ với vận tốc 325m/s.

Một viên đạn có khối lượng m=2kg khi bay đến điểm cao nhất của quỹ đạo parabol với vận tốc v=200m/s theo phương nằm ngang thì nổ thành hai mảnh. Một mảnh có khối lượng m₁=1,5kg văng thẳng đứng xuống dưới với vận tốc v₁ cũng bằng 200m/s. Hỏi mảnh kia bay theo hướng nào và với vận tốc bằng bao nhiêu?

Phương pháp giải

- Áp dụng định luật bảo toàn động lượng:

\(\vec p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \) tính vận tốc của mảnh đạn theo công thức:

\({{v_2} = \frac{{{p_2}}}{{{m_2}}}}\)

- Để xác định hướng bay của mảnh đạn, ta áp dụng công thức:

\({\tan \alpha = \frac{{{p_1}}}{p}}\)

Hướng dẫn giải

p = mv = 2.200 = 400(kgm/s).

p₁ = m1v1 = 1,5.200 = 300(kgm/s);

m₂ = m - m₁ = 0,5(kg)

- Coi hệ “đạn nổ” là hệ kín trong thời gian nổ, áp dụng định luật bảo toàn động lượng :

\(\vec p = \overrightarrow {{p_1}} + \overrightarrow {{p_2}} \)

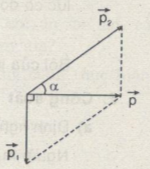
- Từ hình vẽ, ta có:

\(\begin{array}{*{20}{c}} {}&{{p_2} = \sqrt {p_1^2 + {p^2}} = \sqrt {{{300}^2} + {{400}^2}} = 500(kgm/s)}\\ {}&{{v_2} = \frac{{{p_2}}}{{{m_2}}} = \frac{{500}}{{0,5}} = 1000(kgm/s)}\\ {}&{\tan \alpha = \frac{{{p_1}}}{p} = \frac{3}{4} \Rightarrow \alpha = {{37}^0}.} \end{array}\)

Mảnh hai bay lên theo hướng hợp với hướng chuyển động ban đầu góc α=37⁰ với tốc độ 1000m/s.