Giải bài tập SGK Vật lý 10 Nâng cao Bài 22: Lực hướng tâm và lực quán tính li tâm. Hiện tượng tăng, giảm, mất trọng lực

Hãy chọn câu đúng

Các nhà du hành vũ trụ trên con tàu quay quanh Trái Đất ở trong trạng thái mất trọng lượng là do

A. Con tàu ở rất xa Trái Đất nên lực hút của Trái Đất giảm đáng kể.

B. Con tàu ở vào vùng mà lực hút của Trái Đất và lực hút của Mặt Trăng cân bằng nhau.

C. Con tàu đã thoát ra khỏi khí quyển Trái Đất.

D. Các nhà du hành khách và con tàu cùng “rơi” về Trái Đất với gia tốc g nên không còn lực của người đè vào sàn tàu.

Phương pháp giải

Khi con tàu ở ngoài vũ trụ thì lực hấp dẫn của con tàu với Trái Đất cũng chính là lực quán tính hướng tâm của Trái Đất tác dụng lên con tàu

Hướng dẫn giải

- Các nhà du hành và con tàu chịu tác dụng của lực hấp dẫn và lực quán tính cân bằng nhau:

\(\vec P = \overrightarrow {{F_{h{\rm{d}}}}} + \overrightarrow {{F_{qt}}} = m\vec a - m\vec a = 0\)

- Chọn D

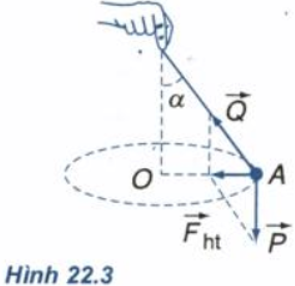
Trong thí nghiệm ở Hình 22.3, dây dài 0,5 m. Hãy tính số vòng quay trong 1 s để dây lệch đi góc α=60⁰ so với phương thẳng đứng.

Phương pháp giải

- Áp dụng định lực II Niuton để xác định lực tác dụng lên dây

- Tính lực hướng tâm theo các công thức:

+ \({F_{ht}} = P.\tan \alpha = mg\tan \alpha \)

+ \({F_{ht}} = m{\left( {2\pi n} \right)^2}.l\sin \alpha \)

- Số vòng dây quay trong 1s được tính theo công thức:

\(n = \sqrt {\frac{{g.\tan \alpha }}{{4{\pi ^2}l.\sin \varepsilon }}} \)

Hướng dẫn giải

Xét vật m trong hệ quy chiếu gắn với Trái Đất.

- Áp dụng định luật II:

\(\overrightarrow {{F_{ht}}} = m\overrightarrow {{a_{ht}}} = \vec T + \vec P\)

- Từ hình vẽ ta thấy: 

\({F_{ht}} = P.\tan \alpha = mg\tan \alpha (1)\)

- Lại có: \({F_{ht}} = m{\omega ^2}R = m{\left( {2\pi n} \right)^2}.R\) với n là tần số vòng

- Trong tam giác vuông OIA có:

\(\begin{array}{l} OA = IA.\sin \alpha \,\,hay\,\,R = l.\sin \alpha \\ \Rightarrow {F_{ht}} = m{\left( {2\pi n} \right)^2}.l\sin \alpha (2) \end{array}\)

- Từ (1) và (2) ta có:

\(\begin{array}{*{20}{l}} {g\tan \alpha = {{\left( {2\pi n} \right)}^2}l\sin \alpha }\\ \begin{array}{l} \Rightarrow n = \sqrt {\frac{{g.\tan \alpha }}{{4{\pi ^2}l.\sin \varepsilon }}} \\ = \frac{1}{{2\pi }}\sqrt {\frac{g}{{l\cos \alpha }}} = 1 vòng/s \end{array} \end{array}\)

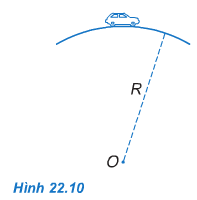
Một ô tô khối lượng m = 1200 kg (coi là chất điểm), chuyển động với vận tốc 36 km/h trên chiếc cầu vồng lên coi như cung tròn có bán kính R = 50 (m) (Hình 22.10). Tính áp lực của ô tô vào mặt cầu tại điểm cao nhất.

Nếu cầu võng xuống (các số liệu vẫn giữ như trên) thì áp lực của ô tô vào mặt cầu tại điểm thấp nhất là bao nhiêu ?

So sánh hai đáp số và nhận xét. 

Phương pháp giải

a) Tính áp lực của ô tô vào mặt cầu tại điểm cao nhất theo cách sau:

- Phân tích lực và áp dụng định luật II Niuton

- Áp dụng công thức:

\(N = m\left( {g - \frac{{{v^2}}}{R}} \right)\) để tính áp lực

b) Tính áp lực của ô tô vào mặt cầu ở vị trí thấp nhất của cầu võng theo công thức sau:

\(N' = N = m(g + \frac{{{v^2}}}{R}){\mkern 1mu} \)

c) Dựa vào kết quả câu a, b và so sánh

Hướng dẫn giải

a) Coi xe là vật chuyển động tròn đều trên cung tròn tâm O bán kính R. Lực phát động cân bằng với lực ma sát. Ở vị trí cao nhất \(\vec P;\vec N\) đều thẳng đứng, qua O nên

\(m\overrightarrow {{a_{ht}}} = \overrightarrow {{F_{ht}}} = \vec P + \vec N{\mkern 1mu} (1)\)

Chọn chiều dương hướng tâm thì

\(\begin{array}{l} (1){\mkern 1mu} = > \frac{{m{v^2}}}{R} = P - N = mg - N\\ = > N = m\left( {g - \frac{{{v^2}}}{R}} \right) = 1200\left( {9,81 - \frac{{{{10}^2}}}{{50}}} \right) = 9372{\mkern 1mu} (N) \end{array}\)

Theo định luật III: Áp lực của ô tô vào mặt cầu tại điểm cao nhất

\(N' = N = 9372{\mkern 1mu} N > mg\)

b) Ở vị trí thấp nhất của cầu võng thì

\(\begin{array}{l} \frac{{m{v^2}}}{R} = N - P = N - mg\\ N' = N = m(g + \frac{{{v^2}}}{R}){\mkern 1mu} = 14172{\mkern 1mu} N > mg \end{array}\)

c) Nhận xét : Áp lực ô tô lên cầu vồng nhỏ hơn lên cầu võng.

Vì lí do này (và còn một số lí do khác ) người ta không làm cầu võng.

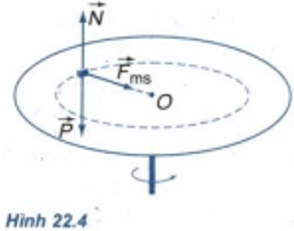
Trong thí nghiệm ở Hình 22.4 , nếu hệ số ma sát nghỉ giữa vật và mặt bàn là 0,25 và tốc độ góc của bàn là 3 rad/s thì có thể đặt vật ở vùng nào trên mặt bàn để nó không bị trượt đi ?

Phương pháp giải

- Áp dụng công thức:

\(R = \frac{{{\mu _n}g}}{{{\omega ^2}}}\) để tính bán kính hình tròn của bàn

- Để vật không trượt thì khoảng cách từ vị trí đăt vật tới trục quay không được lớn hơn bán kính bàn

Hướng dẫn giải

Khi vật không trượt trên mặt bàn quay ta có :

\(\begin{array}{l} {F_q} = {F_{msn}} \le {F_M}\\ mR{\omega ^2} \le {\mu _n}.mg\\ R \le \frac{{{\mu _n}g}}{{{\omega ^2}}} = \frac{{0,25.9,81}}{{{3^2}}} \approx 0,273{\mkern 1mu} (m) \end{array}\)

Vậy để vật không trượt, phải đặt vật trong phạm vi hình tròn có tâm là giao điểm của trục quay với bàn, bán kính là 0,273 m.