Giải bài tập SGK Vật lý 10 Nâng cao Bài 37: Định luật bảo toàn cơ năng
Mời các em cùng eLib củng cố kiến thức về định luật bảo toàn cơ năng, các kỹ năng làm bài tập với tài liệu Giải bài tập SGK Vật lý 10 Nâng cao Bài 37. Nội dung chi tiết tham khảo tại đây. Chúc các em học tốt!
Mục lục nội dung

1. Giải bài 1 trang 177 SGK Vật lý 10 Nâng cao
Một quả bóng được ném với vận tốc đầu xác định. Đại lượng nào không đổi trong khi quả bóng chuyển động.
A. Thế năng
B. Động lượng
C. Động năng
D. Gia tốc
Phương pháp giải
Khi vật rời khỏi tay, vật chỉ chịu tác dụng của trọng lực, do đó gia tốc của vật bằng gia tốc trọng trường
Hướng dẫn giải
- Khi ném quả bóng có vận tốc đầu xác định thì đại lượng không đổi trong quá trình bóng chuyển động là gia tốc
- Chọn đáp án D.
2. Giải bài 2 trang 177 SGK Vật lý 10 Nâng cao
Một hòn bi có khối lượng 20g được ném thẳng đứng lên cao với vật tốc 4m/s từ độ cao 1,6m so với mặt đất.
a) Tính trong hệ quy chiếu mặt đất các giá trị động năng, thế năng và cơ năng của hòn bi tại lúc ném vật.
b) Tìm độ cao cực đại mà bi đạt được
Phương pháp giải
a) Áp dụng công thức:
- \({{W_d} = \frac{{mv_{}^2}}{2}}\) để tính động năng của vật
- \({{W_t} = mgz}\) để tính thế năng của vật
- Cơ năng được tính theo công thức: \({{W_{}} = {W_d} + W}\)
b) Độ cao cực đại được tính theo công thức: zmax = W1/mg
Hướng dẫn giải
a) Trong hệ quy chiếu mặt đất, lúc ném hòn bi có:
\(\begin{array}{l} {W_{d1}} = \frac{{mv_1^2}}{2} = \frac{{0,{{02.4}^2}}}{2} = 0,160(J);\\ {W_{t1}} = mg{z_1} = 0,02.9,8.1,6 \approx 0,314(J)\\ \Rightarrow {W_1} = {W_{d1}} + {W_{t1}} = 0,16 + 0,31 = 0,474(J) \end{array}\)
b) Áp dụng định luật bảo toàn cơ năng cho hai vị trí: vị trí ném và vị trí cao nhất (v2=0):
3. Giải bài 3 trang 177 SGK Vật lý 10 Nâng cao
Một con lắc đơn có chiều dài l= 1m. kéo cho dây làm với đường thẳng đứng góc \(\alpha = {45^0}\) rồi thả tự do. Tìm vận tốc của con lắc khi nó đi qua:
a) Vị trí ứng với góc 30o
b) Vị trí cân bằng
Phương pháp giải
Để tìm vận tốc của con lắc, ta làm theo cách sau:
- Tính thế năng theo công thức: Wt\(= mgl(1 - \cos \alpha ) \)
- Tính động năng theo công thức: \({{\rm{W}}_d} = \frac{{m{v^2}}}{2}\)
- Áp dụng định luật bảo toàn cơ năng, rút ra được công thức tính vận tốc là:
\({v = \sqrt {2gl(cos\alpha - cos{\alpha _0})} }\)
Thay giá trị góc tương ứng với câu a, b
Hướng dẫn giải
Chọn \({{\rm{W}}_{{t_0}}} = 0\) thì cơ năng tại \(A({\alpha _0})\) là :
\({\rm{W}} = {{\rm{W}}_{{t_A}}} = mg{z_A} = mg(l - l\cos {\alpha _0})\)
- Thế năng tại \(B(\alpha ):\;\,{{\rm{W}}_t}\) \(= mgl(1 - \cos \alpha ) \)
- Động năng tại B: \({{\rm{W}}_d} = \frac{{m{v^2}}}{2}\)
- Áp dụng định luật bảo toàn cơ năng:
\(\begin{array}{l} {W_B} = {W_A}\\ \Leftrightarrow {W_t} + {W_d} = W\\ \Leftrightarrow mgl(l - cos\alpha ) + \frac{{m{v^2}}}{2} = mgl(1 - cos{\alpha _0})\\ \Rightarrow v = \sqrt {2gl(cos\alpha - cos{\alpha _0})} \end{array}\)
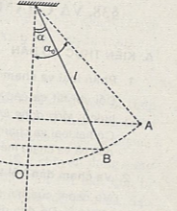
\(\begin{array}{l} a)\,\,\alpha = {30^0} \Rightarrow v = \sqrt {2.9,8.1\left( {\frac{{\sqrt 3 }}{2} - \frac{{\sqrt 2 }}{2}} \right)} \\ \Rightarrow v \approx 1,76(m/s)\\ b)\,\,\alpha = {0^0} \Rightarrow v = \sqrt {2.9,8.2\left( {1 - \frac{{\sqrt 2 }}{2}} \right)} \\ \Rightarrow v \approx 2,40(m/s) \end{array}\)
4. Giải bài 4 trang 177 SGK Vật lý 10 Nâng cao
Một vật được ném từ mặt đất với vận tốc 10m/s hướng chếch lên phía trên, với các góc ném hợp với phương nằm ngang lần lượt là 30o và 60o. Bỏ qua sức cản của không của không khí. Vận tốc chạm đất của vật trong mỗi lần ném thay đổi ra sao? Độ cao cực đại mà vật đạt được trong mỗi trường hợp bằng bao nhiêu?
Hướng dẫn: Dùng định luật bảo toàn cơ năng để giải, có kết hợp với phương pháp động lực học.
Phương pháp giải
a) Vì cơ năng được bảo toàn nên vận tốc chạm đất trong hai trường hợp bằng nhau
b) Để tính độ cao cực đại, ta sử dụng công thức:
\({{z_{\max }} = \frac{{{{\left( {{v_0}\sin \alpha } \right)}^2}}}{{2g}}}\)
⇒ Áp dụng công thức trên cho mỗi trường hợp
Hướng dẫn giải
a) Coi mặt đất là mặt phẳng ngang. Chọn Wt=0 tại mặt đất.
Bỏ qua lực cản không khí thì cơ năng được bảo toàn, suy ra:
\(\begin{array}{l} {{\rm{W}}_{{d_2}}} = {{\rm{W}}_{{d_1}}} = {{\rm{W}}_{{d_0}}}\\ hay\,\,\,\,{v_2} = {v_1} = {v_0} = 10(m/s) \end{array}\)
Trong cả hai trường hợp với vận tốc chạm đất của vật đều có độ lớn bằng vận tốc ném nhưng khác nhau ở góc rơi:
\(\left\{ \begin{array}{l} {\beta _1} = {\alpha _1} = {30^0}\\ {\beta _2} = {\alpha _2} = {60^0} \end{array} \right.\)
b) Khi đạt độ cao cực đại thì vật có: \(v = {v_x} = {v_0}\cos \alpha .\)
Áp dụng định luật bảo toàn cơ năng :
\(\begin{array}{l} mg{z_{\max }} + \frac{1}{2}m{({v_0}\cos \alpha )^2} = \frac{1}{2}(mv_0^2)\\ \Rightarrow {z_{\max }} = \frac{{{{\left( {{v_0}\sin \alpha } \right)}^2}}}{{2g}} \end{array}\)
Với \( {\alpha _1} = {30^0}:\,\,\,{z_{1\max }} = \frac{{{{\left( {10.0,5} \right)}^2}}}{{2.9,8}} \approx 1,28(m)\)
Với \(\alpha = {60^0}:\,\,\,{z_{2\max }} = \frac{{{{\left( {10.\frac{{\sqrt 3 }}{2}} \right)}^2}}}{{2.9,8}} \approx 3,83(m)\)
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 31: Định luật bảo toàn động lượng
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 32: Chuyển động bằng phản lực. Bài tập về định luật bảo toàn động lượng
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 33: Công và công suất
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 34: Động năng. Định lí động năng
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 35: Thế năng. Thế năng trọng trường
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 36: Thế năng đàn hồi
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 38: Va chạm đàn hồi và không đàn hồi
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 40: Các định luật Kê-ple. Chuyển động của vệ tinh
