Giải bài tập SGK Vật lý 10 Nâng cao Bài 23: Bài tập về động lực học
Nội dung hướng dẫn Giải bài tập Lý 10 Nâng cao Bài 23 dưới đây do eLib biên soạn sẽ giúp các em học sinh nắm vững phương pháp giải bài tập về động lực học. Mời các em tham khảo!
Mục lục nội dung

1. Giải bài 1 trang 106 SGK Vật lý 10 Nâng cao
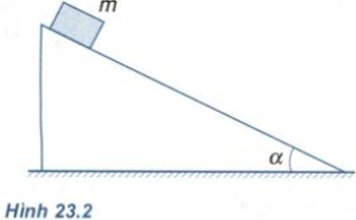
Vật khối lượng m đặt trên mặt phẳng nghiêng hợp với phương nằm ngang một góc α (Hình 23.2). Hệ số ma sát trượt giữa vật và mặt phẳng nghiêng là μt. Khi được thả ra, vật trượt xuống. Gia tốc của vật phụ thuộc vào những đại lượng nào ?
A. μt, m, α B. μt,g,α
C. m,g,μt D. m,g,μt,α
Phương pháp giải
Dựa vào biểu thức tính gia tốc để tìm các đại lượng mà gia tốc phụ thuộc
Hướng dẫn giải
- Biểu thức gia tốc:
\(a = g(\sin \alpha - {\mu _t}{\rm{cos}}\alpha )\)
⇒ Gia tốc của vật phụ thuộc vào hệ số ma sát trượt μt, gia tốc trọng trường g và góc nghiêng α
- Chọn B
2. Giải bài 2 trang 106 SGK Vật lý 10 Nâng cao
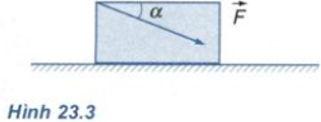
Một cái hòm khối lượng m = 40 kg đặt trên sàn nhà. Hệ số ma sát trượt giữa hòm và sàn nhà là μt=0,2. Người ta đẩy hòm bằng một lực F =200N theo phương hợp với phương nằm ngang một góc α=300, chếch xuống phía dưới (Hình 23.3). Tính gia tốc của hòm.
Phương pháp giải
- Phân tích lực và áp dụng định luật II Niuton
- Tính lực ma sát theo công thức:
\({F_{ms}} = {\mu _t}N\)
- Gia tốc vật được tính theo công thức:
\(a = \frac{{F{\rm{cos}}\alpha - {F_{ms}}}}{m}\)
Hướng dẫn giải
m=40kg; α=300; μt=0,2.
F=200N; g=9,8(m/s2)
Vật chịu tác dụng của 4 lực được biểu diễn như hình vẽ.
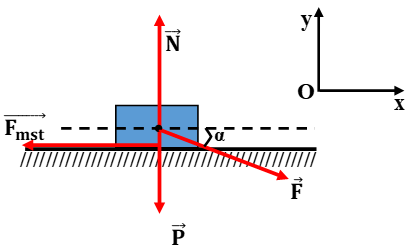
- Áp dụng định luật Niu -tơn II ta có :
\(\vec a = \frac{{\vec P + \vec N + \vec F + \overrightarrow {{F_{msn}}} }}{m}(1)\)
- Chiếu (1) lên trục Oy được :
\(\begin{array}{l} N = mg + F\sin \alpha \\ = 40.9,8 + 200.0,5 = 492(N)\\ {F_{ms}} = {\mu _t}N = 0,2.492 = 98,4(N) \end{array}\)
- Chiếu (1) lên Ox được :
\(\begin{array}{l} a = \frac{{F{\rm{cos}}\alpha - {F_{ms}}}}{m}\\ = \frac{{200\frac{{\sqrt 3 }}{2} - 98,4}}{{40}} = 1,87(m/{s^2}) \end{array}\)
3. Giải bài 3 trang 106 SGK Vật lý 10 Nâng cao
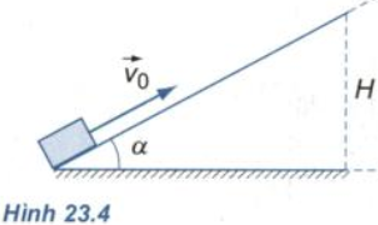
Một vật đặt trên mặt phẳng nghiêng (góc nghiêng α = 300), được truyền một vận tốc ban đầu v0=2m/s (Hình 23.4). Hệ số ma sát giữa vật và mặt phẳng nghiêng là 0,3.
a) Tính gia tốc của vật.
b) Tính độ cao lớn nhất (Hmax) mà vật đạt tới.
c) Sau khi đạt tới độ cao Hmax, vật sẽ chuyển động như thế nào ?
Phương pháp giải
a) Tính gia tốc của vật theo công thức:
\(a = - g\left( {\sin \alpha + {\mu _t}{\rm{cos}}\alpha } \right)\)
b) Áo dụng công thức:
\({H_{\max }} = S.\sin \alpha = \frac{{ - {v_0}^2\sin \alpha }}{{2a}}\) để tính độ cao lớn nhất
c) Để biết tính chất chuyển động của vật khi ở độ cao Hmax ta tính gia tốc theo công thức:
\(a' = g(\sin \alpha - {\mu _t}{\rm{cos}}\alpha )\)
Hướng dẫn giải
α=300; v0=2m/s; μt=0,3
Chọn gốc tọa độ O là điểm truyền vận tốc v0, chiều trục như hình vẽ.
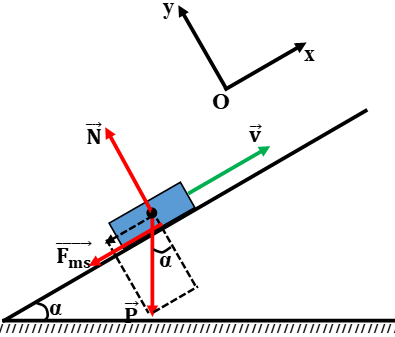
a) Gia tốc của vật:
\(\begin{array}{l} a = - g\left( {\sin \alpha + {\mu _t}{\rm{cos}}\alpha } \right)\\ = - 9,8\left( {0,5 + 0,3\frac{{\sqrt 3 }}{2}} \right) = - 7,45(m/{s^2}) \end{array}\)
b) Khi đạt độ cao cực đại thì vật có v = 0 nên quãng đường đi được tới lúc đó là
\(\begin{array}{l} S = \frac{{ - v_0^2}}{{2a}}\\ \Rightarrow {H_{\max }} = S.\sin \alpha = \frac{{ - {v_0}^2\sin \alpha }}{{2a}}\\ = \frac{{ - {2^2}.0,5}}{{2.( - 7,45)}} \approx 0,134(m) = 13,4cm \end{array}\)
c) Coi μn=μt=0,3. Tại vị trí cao nhất, lực ma sát chuyển thành ma sát nghỉ, chiều dương hướng lên.
So sánh hai thành phần lực Px và Fmsn ta thấy:
\(\frac{{{P_x}}}{{{F_{ms}}}} = \frac{{mg\sin \alpha }}{{{\mu _n}mg\cos \alpha }}{\mkern 1mu} = \frac{{\tan \alpha }}{{{\mu _n}}}{\mkern 1mu} = \frac{1}{{0,3\sqrt 3 }} > 1\)
Vậy vật đổi chiều chuyển động, chuyển động nhanh dần đều xuống với gia tốc khác:
\(a' = g(\sin \alpha - {\mu _t}{\rm{cos}}\alpha ) \approx - 2,35({\rm{m}}/{{\rm{s}}^2})\)
4. Giải bài 4 trang 106 SGK Vật lý 10 Nâng cao
Một con lắc gồm một quả cầu nhỏ khối lượng m=200 g treo vào sợi dây chiều dài l=15 cm, buộc vào đầu một cái cọc gắn với mép một cái bàn quay (Hình 23.5). Bàn có bán kính r = 20 cm và quay với vận tốc không đổi.
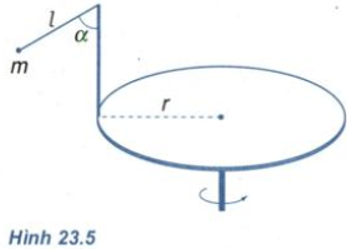
a) Tính số vòng quay của bàn trong 1 min để dây nghiêng so với phương thẳng đứng một góc α=600
b) Tính lực căng của dây trong trường hợp của câu a).
Phương pháp giải
a) Tính số vòng quay trong 1 min theo công thức: n=60f
với tần số là: \(f = \frac{1}{{2\pi }}\sqrt {\frac{{g\tan \alpha }}{R}} \)
b) Áp dụng công thức:
\(T = \frac{P}{{{\rm{cos}}\alpha }} = \frac{{mg}}{{{\rm{cos}}\alpha }}\) để tính lực căng dây
Hướng dẫn giải
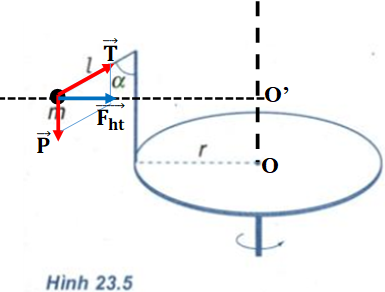
a) Khi bàn quay đều với vận tốc góc ωω thì chất điểm m chuyển động tròn đều trên một đường tròn nằm ngang tâm O’.
- Bán kính quỹ đạo:
\(R = r + l\sin \alpha = 0,2 + 0,15\frac{{\sqrt 3 }}{2} \approx 0,33{\mkern 1mu} m\)
- Lực hướng tâm là hợp của \(\vec P{\mkern 1mu} và {\mkern 1mu} \vec T{\mkern 1mu} \,\,nên{\mkern 1mu} \overrightarrow {\,\,{F_{ht}}} = \vec P + \vec T\)
\(\begin{array}{l} \Rightarrow {F_{ht}} = P.\tan \alpha \\ \Rightarrow mR{\omega ^2} = mg.\tan \alpha \\ \Rightarrow R{(2\pi f)^2} = g\tan \alpha \\ \Rightarrow f = \frac{1}{{2\pi }}\sqrt {\frac{{g\tan \alpha }}{R}} \\ = \frac{1}{{2.3,14}}.\sqrt {\frac{{9,8.\sqrt 3 }}{{0,33}}} = 1,142Hz \end{array}\)
Số vòng quay trong 1 min: \(n = 60f = 68,5\) (v/min)
b) Lực căng dây là:
\(T = \frac{P}{{{\rm{cos}}\alpha }} = \frac{{mg}}{{{\rm{cos}}\alpha }} = \frac{{0,2.9,8}}{{0,5}} = 3,92(N)\)
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 13: Lực. Tổng hợp và phân tích lực
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 14: Định luật I Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 15: Định luật II Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 16: Định luật III Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 17: Lực hấp dẫn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 18: Chuyển động của vật bị ném
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 19: Lực đàn hồi
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 20: Lực ma sát
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 21: Hệ quy chiếu có gia tốc. Lực quán tính
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 22: Lực hướng tâm và lực quán tính li tâm. Hiện tượng tăng, giảm, mất trọng lực
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 24: Chuyển động của hệ vật
- doc Giải bài tập SGK Vật lý 10 nâng cao Bài 25: Thực hành: Xác định hệ số ma sát
