Giải bài tập SGK Vật lý 10 Nâng cao Bài 6: Sự rơi tự do

Chọn câu sai

A. Khi vật rơi tự do mọi vật chuyển động hoàn toàn như nhau

B. Vật rơi tự do khi không chịu sức cản của không khí

C. Người nhảy dù trên hình 6.2  đang rơi tự do

D. Mọi vật chuyển động gần mặt dất đều chịu gia tốc rơi tự do

Phương pháp giải

Để trả lời câu hỏi này cần nắm được đặc điểm của vật rơi tự do

Hướng dẫn giải

- Vì theo hình bên người nhảy dù rơi nằm ngang, dang tay, làm cho lực cản của không khí là đáng kể, do đó không được coi là rơi tự do.

- Chọn C

Một vật rơi tự do không vận tốc đầu từ độ cao 5 m. Tìm vận tốc của nó khi chạm đất

Phương pháp giải

Áp dụng công thức:

\(v = \sqrt {2gh} \) để tính vận tốc

Hướng dẫn giải

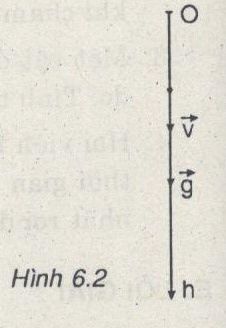
Chọn hệ tọa độ như hình vẽ: gốc O ≡ điểm thả vật     

Gốc thời gian là lúc thả vật. Lấy g = 9,8 m/s² (h.6.2)

Vận tốc khi chạm đất là:

\(v = \sqrt {2gh} = \sqrt {2.9,8.5} = 9,9(m/s)\)

Một vật được thả từ trên máy bay ở độ cao 80m. Cho rằng vật rơi tự do. Tính thời gian rơi.

Phương pháp giải

Áp dụng công thức:

\(t = \sqrt {\frac{{2h}}{g}} \) để tính thời gian rơi

Hướng dẫn giải

Rơi tự do từ độ cao h=80 m so với đất.

Thời gian rơi:

\(t = \sqrt {\frac{{2h}}{g}} = \sqrt {\frac{{2.80}}{{9,8}}} \approx 4,04(s)\)

Hai viên bi sắt được thả rơi từ cùng một độ cao cách nhau một khoảng thời gian 0,5s. Tính khoảng thời gian cách nhau giữa hai viên bi sau khi viên bi thứ nhất được rơi được 1s; 1,5s

Phương pháp giải

Để tính khoảng cách giữa hai viên bi ta làm theo cách sau:

- Lập phương trình chuyển động của hai vật theo dạng: h=1/2gt²

- Phương trình khỏang cách hai vật là: 

\(\begin{array}{l} \left| {{\rm{\Delta }}h} \right| = {h_1} - {h_2} \end{array}\)

- Thay các giá trị thời gian t tương ứng vào phương trình khoảng cách

Hướng dẫn giải

Chọn hệ tọa độ gốc O trùng với điểm thả vật, gốc thời gian là lúc vật I bắt đầu rơi

- Phương trình chuyển động của vật I :

\({h_1} = \frac{{g{t^2}}}{2} = 4,9{t^2}(s;m)\)

- Phương trình chuyển động của vật II:

\({h_2} = \frac{{g{{(t - 0,5)}^2}}}{2} = 4,9{(t - 0,5)^2}(s;m)\)

- Khoảng cách hai vật:

\(\begin{array}{l} \left| {{\rm{\Delta }}h} \right| = {h_1} - {h_2} = 4,9{t^2} - 4,9{(t - 0,5)^2}\\ = 4,9t - 1,225(s;m) \end{array}\)

- Tại t = 1s thì 

\(\left| {{\rm{\Delta }}h} \right| = 4,9.1 - 1,225 = 3,675(m)\)

- Tại t = 1,5s thì

\(\left| {{\rm{\Delta }}h} \right| = 4,9.1,5 - 1,225 = 6,125(m)\)