Giải bài tập SGK Vật lý 10 Nâng cao Bài 24: Chuyển động của hệ vật
Mời các em cùng eLib củng cố kiến thức và rèn luyện phương pháp Giải bài tập: Chuyển động của hệ vật trong nội dung SGK Vật lý 10 Nâng cao Bài 28. Nội dung chi tiết tham khảo tại đây. Chúc các em học tốt!
Mục lục nội dung

1. Giải bài 1 trang 109 SGK Vật lý 10 Nâng cao
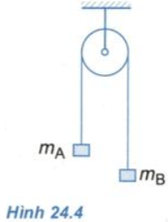
Cho hệ vật như ở Hình 24.4. Biết mA>mB. Gia tốc của hai vật là a. Lực căng dây bằng bao nhiêu?
A. mAg B. (mA+mB)
C. (mA−mB)g D. mA(g−a)
Phương pháp giải
Tính lực căng dây tác dụng lên vật theo công thức:
\(T = {m_{}}\left( {g - a} \right)\)
Hướng dẫn giải
- Áp dụng định luật II cho vật mA:
\(\begin{array}{l} {m_A}\vec a = {m_A}\vec g + \vec T\\ \Rightarrow {m_A}a = {m_A}g - T \Rightarrow T = {m_A}\left( {g - a} \right) \end{array}\)
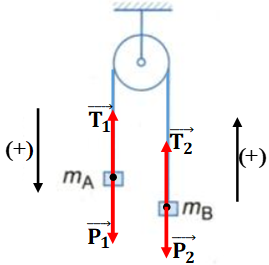
- Chọn D
2. Giải bài 2 trang 109 SGK Vật lý 10 Nâng cao
Một đầu tàu có khối lượng 50 tấn được nối với hai toa, mỗi toa có khối lượng 20 tấn. Đoàn tàu bắt đầu chuyển động với gia tốc a = 0,2 m/s2. Hệ số ma sát lăn giữa bánh xe với đường ray là 0,05. Hãy tính:
a) Lực phát động tác dụng lên đoàn tàu.
b) Lực căng ở những chỗ nối toa.
Phương pháp giải
a) Tính lực phát động tác dụng lên đoàn tàu theo công thức:
\(F = (m + {m_1} + {m_2})(a + \mu g)\)
b) Áp dụng công thức:
- \({T_2} = {m_2}(a + \mu g)\) để tính lực căng chỗ nối toa 2 và 3
- \({T_1} = {m_1}(a + \mu g) + T\) để tính lực căng chỗ nối toa 1 và 2
Hướng dẫn giải
a) Đường ngang nên
\({F_{ms}} = \mu mg;{\mkern 1mu} \,\,\,{F_{ms1}} = \mu {m_1}g{\mkern 1mu} ;{\mkern 1mu} \,\,\,{F_{ms2}} = \mu {m_2}g\)

Áp dụng định luật II cho hệ vật:
\(\begin{array}{l} a = \frac{{F - {F_{ms}} - {F_{ms1}} - {F_{ms2}}}}{{m + {m_1} + {m_2}}}\\ = \frac{{F - \mu g(m + {m_1} + {m_2})}}{{m + {m_1} + {m_2}}}\\ F = (m + {m_1} + {m_2})(a + \mu g) = 62100{\mkern 1mu} N \end{array}\)
b) Áp dụng định luật II cho toa 2:
\(\begin{array}{l} {m_2}a = {T_2} - {F_{ms2}} = {T_2} - \mu {m_2}g\\ {T_2} = {m_2}(a + \mu g) = 13800{\mkern 1mu} (N) \end{array}\)
Áp dụng định luật cho toa 1:
\(\begin{array}{l} {m_1}a = {T_1} - {F_{ms1}} - {T_2} = {T_1} - \mu {m_1}g - {T_2}\\ {T_1} = {m_1}(a + \mu g) + {T_2} = 27600{\mkern 1mu} N \end{array}\)
3. Giải bài 3 trang 109 SGK Vật lý 10 Nâng cao
Người ta vắt qua một chiếc ròng rọc nhẹ một đoạn dây, ở hai đầu có treo hai vật A và B có khối lượng là mA=260 g và mB=240 g (Hình 24.4). Thả cho hệ bắt đầu chuyển động.
.png)
a) Tính vận tốc của từng vật ở cuối giây thứ nhất.
b) Tính quãng đường mà từng vật đi được trong giây thứ nhất.
Bỏ qua ma sát ở ròng rọc, coi dây là không dãn.
Phương pháp giải
a) Áp dụng công thức: v=a.t để tính vận tốc
b) Áp dụng công thức: s=1/2a.t2 để tính quãng đường đi được
Hướng dẫn giải
\({v_0} = 0;\,\,\,a = \frac{{({m_A} - {m_B})g}}{{{m_A} + {m_B}}} = 0,392(m/{s^2})\)
Chọn chiều dương của vật A là đi xuống, cho vật B đi lên, ta có:
a) Vận tốc mỗi vật ở cuối giây thứ nhất:
\({v_A} = {v_B} = {v_1} = a{t_1} = 0,392.1 = 0,392(m/s)\)
b) Quãng đường vật ở cuối giây thứ nhất:
\({S_A} = {S_B} = {S_1} = \frac{{at_1^2}}{2} = 0,196(m)\)
4. Giải bài 4 trang 109 SGK Vật lý 10 Nâng cao
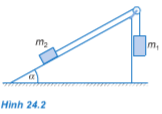
Trong ví dụ ở mục 2 của bài, nếu cho m1 những giá trị khác nhau (các dữ kiện khác giữ nguyên) thì hiện tượng có thể diễn ra những khả năng nào? Tìm phạm vi giá trị của m1 để xảy ra mỗi khả năng ấy.
Dưới đây là thông tin về mục 2 của bài:
- Dữ kiện: \({m_2} = 200g;\,\,\alpha = {30^o};\,\,{u_t} = 0,3\)
- Hình vẽ:
Phương pháp giải
Vận dụng tính chất:
- Vật 1 đi xuống nếu: \({P_1} > {P_{2x}} + {F_M}\)
- Vật 1 đi lên nếu: P2x > P1+FM
Để tìm khoảng giới hạn m1
Hướng dẫn giải
Với giả thiết \({\mu _n} = {\mu _t} = 0,3\) thì:
- m1 sẽ đi xuống nếu \({P_1} > {P_{2x}} + {F_M}\)
⇔ m1g > m2gsinα + μnm2gcosα
⇒ m1 > m2(sinα+μncosα)m1 >152g
- m1 đi lên nếu P2x > P1+FM
⇔ P1 < P2x− FM
⇔ m1g <m2gsinα−μnm2gcosα
⇔ m1<m2(sinα−μncosα)
⇔ m1<48g
- m1 đứng yên nếu 48 ≤ m≤ 152(g)
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 13: Lực. Tổng hợp và phân tích lực
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 14: Định luật I Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 15: Định luật II Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 16: Định luật III Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 17: Lực hấp dẫn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 18: Chuyển động của vật bị ném
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 19: Lực đàn hồi
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 20: Lực ma sát
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 21: Hệ quy chiếu có gia tốc. Lực quán tính
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 22: Lực hướng tâm và lực quán tính li tâm. Hiện tượng tăng, giảm, mất trọng lực
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 23: Bài tập về động lực học
- doc Giải bài tập SGK Vật lý 10 nâng cao Bài 25: Thực hành: Xác định hệ số ma sát