Giải bài tập SGK Vật lý 10 Nâng cao Bài 18: Chuyển động của vật bị ném
Mời các em cùng eLib củng cố kiến thức và rèn luyện phương pháp giải bài tập chuyển động của vật bị ném với tài liệu Giải bài tập SGK Vật lý 10 Nâng cao Bài 18. Nội dung chi tiết tham khảo tại đây. Chúc các em học tốt!
Mục lục nội dung
1. Giải bài 1 trang 84 SGK Vật lý 10 Nâng cao
2. Giải bài 2 trang 84 SGK Vật lý 10 Nâng cao
3. Giải bài 3 trang 84 SGK Vật lý 10 Nâng cao
4. Giải bài 4 trang 84 SGK Vật lý 10 Nâng cao
5. Giải bài 5 trang 84 SGK Vật lý 10 Nâng cao
6. Giải bài 6 trang 84 SGK Vật lý 10 Nâng cao

1. Giải bài 1 trang 84 SGK Vật lý 10 Nâng cao
Một vật khối lượng m, được ném ngang từ độ cao h với vận tốc ban đầu vo. Tầm bay xa của nó phụ thuộc vào những yếu tố nào ?
A. m và vo B. m và h
C. vo và h C. m, vo và h
Phương pháp giải
Vận dụng công thức tính tầm xa:
\(L = {v_0}\sqrt {\frac{{2h}}{g}} \) để rút ra các đại lượng ảnh hưởng đến L
Hướng dẫn giải
- Khi ném ngang thì \(\alpha = 0 \to x = {v_0}t,y = - \frac{{g{t^2}}}{2};\) lúc tới đất y = -h nên \(t = \sqrt {\frac{{2h}}{g}} {\rm{\; và \;}}L = {v_0}\sqrt {\frac{{2h}}{g}} \)
- Chọn C
2. Giải bài 2 trang 84 SGK Vật lý 10 Nâng cao
Hãy chọn câu đúng
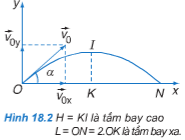
Trong Hình 18.2, gia tốc của vật tại đỉnh I
A. hướng ngang từ trái sang phải.
B. hướng ngang từ phải sang trái.
C. hướng thẳng đứng xuống dưới.
D. bằng 0.
Phương pháp giải
Để trả lời câu hỏi này cần nắm được các đặc điểm về chuyển động ném ngang của một vật
Hướng dẫn giải
- Tại mọi điểm trên quỹ đạo, gia tốc của vật luôn là vì trong suốt thời gian chuyển động, vật chỉ chịu tác dụng của trọng lực có chiều hướng thẳng đứng xuống dưới.
- Chọn C
3. Giải bài 3 trang 84 SGK Vật lý 10 Nâng cao
Một vật được ném từ mặt đất với v0=10m/s và góc ném α. Tính toán và điền kết quả vào bảng sau đây. Lấy g=10m/s2
Phương pháp giải
Áp dụng công thức: \({y = \frac{{ - g{x^2}}}{{2v_0^2{\rm{co}}{{\rm{s}}^2}\alpha }} + \left( {tg\alpha } \right)x}\) cho mỗi góc α tương ứng với giá trị x là tầm xa và giá trị y là tầm bay cao
Hướng dẫn giải
- Nhận xét: Với góc ném α = 45o thì tầm bay xa là lớn nhất
- Trong thực tế, do có lực cản không khí nên các giá trị thực tế thường nhỏ hơn các giá trị trong bảng.
- Trường hợp ném xuôi gió lại có thể có kết quả lớn hơn giá trị trong bảng.
4. Giải bài 4 trang 84 SGK Vật lý 10 Nâng cao
Vẽ quỹ đạo của vật trong bài tập trên cho trường hợp α=450
Phương pháp giải
Dựa vào biểu thức phương trình:
\({y = \frac{{ - g{x^2}}}{{2v_0^2{\rm{co}}{{\rm{s}}^2}\alpha }} + \left( {tg\alpha } \right)x}\) tính một vài giá trị x để tìm y và vẽ hình
Hướng dẫn giải
- Ta có:
\(\begin{array}{l} \alpha = {45^0}{\mkern 1mu} ;{\mkern 1mu} {v_0} = 10{\mkern 1mu} m/s{\mkern 1mu} ;{\mkern 1mu} g = 10{\mkern 1mu} m/{s^2};\\ y = \frac{{ - g{x^2}}}{{2v_0^2{\rm{co}}{{\rm{s}}^2}\alpha }} + \left( {tg\alpha } \right)x{\mkern 1mu} = - 0,1{x^2}{\mkern 1mu} + x{\mkern 1mu} (m) \end{array}\)
- Bảng biến thiên:
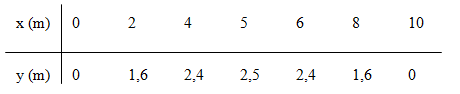
- Hình vẽ:
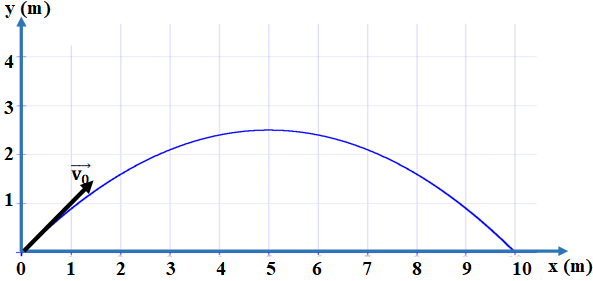
5. Giải bài 5 trang 84 SGK Vật lý 10 Nâng cao
Từ độ cao 15 m so với mặt đất , một vật được ném chếch lên với vectơ vận tốc đầu 20 m/s hợp với phương nằm ngang một góc 300. Hãy tính:
a) Thời gian từ lúc ném đến lúc vật chạm đất.
b) Độ cao lớn nhất ( so với mặt đất ) mà vật đạt tới.
c) Tầm bay xa của vật (khoảng cách từ hình chiếu của điểm ném trên mặt đất đến điểm rơi) . Lấy g=10m/s2
Phương pháp giải
a) Thay y=0 vào phương trình chuyển động của vật để tìm thời gian
b) Áp dụng công thức:
\(H = {y_{\max }} = - \frac{{\rm{\Delta }}}{{4a}} \) để tính độ cao cực đại
c) Tầm bay xa được tính bằng công thức:
\(L = {x_{\max }} \)
Hướng dẫn giải
Chọn Ox ở mặt đất, Oy hướng lên đi qua điểm ném.
\(\begin{array}{l} x = {v_0}c{\rm{os}}\alpha .{\rm{t}}{\mkern 1mu} = 10\sqrt 3 t{\mkern 1mu} (m;s)\\ y = h + ({v_0}\sin \alpha )t - \frac{{g{t^2}}}{2} = 15 + 10t - 5{t^2}(m;s) \end{array}\)
a) Lúc chạm đất:
\(y = 0 \Rightarrow 15 + 10t - 5{t^2} = 0 \Rightarrow t = 3(s)\)
Thời gian bay là 3 (s)
b) Độ cao cực đại:
\(H = {y_{\max }} = - \frac{{\rm{\Delta }}}{{4a}} = - \frac{{{{10}^2} + 4.5.15}}{{4.( - 5)}} = 20{\mkern 1mu} (m)\)
c) Tầm bay xa:
\(L = {x_{\max }} = 10\sqrt 3 .3 \approx 52{\mkern 1mu} m\)
6. Giải bài 6 trang 84 SGK Vật lý 10 Nâng cao
Một vật được ném ngang với vận tốc v0=30(m/s), ở độ cao h = 80 m.
a) Vẽ quỹ đạo chuyển động.
b) Xác định tầm bay xa của vật.
c) Xác định vận tốc của vật lúc chạm đất.
Phương pháp giải
a) Vẽ quỹ đạo như hình bên dưới
b) Tính tầm bay xa của vật theo công thức:
\(L = {x_{\max }} \)
c) Xác định vận tốc của vật lúc chạm đất theo cách:
- Tính thời gian chạm đất:
\(t{\mkern 1mu} = \sqrt {\frac{{2h}}{g}} \)
- Tính vận tốc chạm chạm đất:
\(v = \sqrt {v_0^2 + {{(gt)}^2}} \)
- Tính hướng vật chạm đất theo công thức:
\(tg\alpha = \frac{{{v_y}}}{{{v_0}}}\)
Hướng dẫn giải
a) Vật ném ngang v0=30(m/s) ; h = 80 m.
Chọn Ox tại mặt đất, Oy hướng lên đi qua điểm ném.
- Phương trình quỹ đạo: y=80−x2/180(m)
- Bảng biến thiên:

- Hình vẽ:
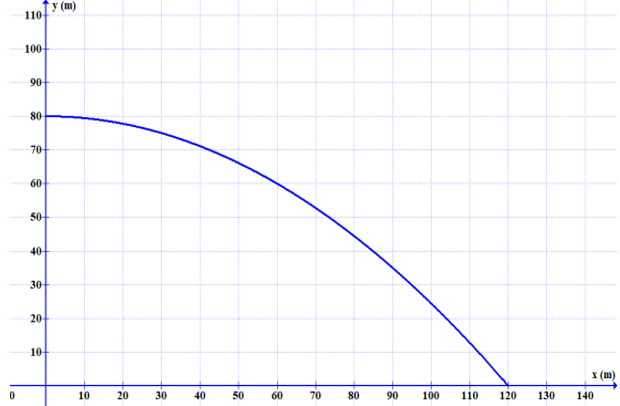
b) Tầm bay xa: Khi y = 0 thì
\(L = {x_{\max }} = \sqrt {180.80} = 120{\mkern 1mu} (m)\)
c) - Thời gian chạm đất:
\(t{\mkern 1mu} = \sqrt {\frac{{2h}}{g}} = 4{\mkern 1mu} (s)\)
- Vận tốc chạm đất:
\(\begin{array}{l} v = \sqrt {v_0^2 + v_y^2} = \sqrt {v_0^2 + {{(gt)}^2}} \\ = \sqrt {{{30}^2} + {{(10.4)}^2}} = 50{\mkern 1mu} (m/s) \end{array}\)
- Hướng vật chạm đất:
\(tg\alpha = \frac{{{v_y}}}{{{v_0}}} = \frac{4}{3} = > \alpha \approx {53^0}\)
7. Giải bài 7 trang 84 SGK Vật lý 10 Nâng cao
Một máy bay theo phương ngang ở độ cao 5 km với vận tốc không đổi 720 km/h. Người trên máy bay muốn thả một vật rơi trúng một đích nào đó trên mặt đất thì phải thả từ cách đích bao xa theo phương nằm ngang ? Bỏ qua lực cản của không khí
Phương pháp giải
Áp dụng công thức:
\(L = {v_0}\sqrt {\frac{{2h}}{g}} \) để tính vị trí thả vật
Hướng dẫn giải
h = 5 km =5000 m; v0=720km/h=200m/s
Bỏ qua lực cản; g=10m/s2
Vật thả từ máy bay ngang là vật bị ném ngang với vận tốc bằng vận tốc của máy bay nên muốn thả trúng đích thì máy bay phải thả vật cách đích (theo phương ngang) 1 khoảng bằng tầm bay xa của vật.
\(L = {v_0}\sqrt {\frac{{2h}}{g}} = 200\sqrt {\frac{{2.500}}{{10}}} \approx 6325{\mkern 1mu} (m)\)
8. Giải bài 8 trang 84 SGK Vật lý 10 Nâng cao
Một vật được ném ngang ở độ cao 20 m phải có vận tốc là bao nhiêu để trước lúc chạm đất vận tốc của nó là 25 m/s ?
Phương pháp giải
Tính vận tốc đầu của vật theo công thức:
\({{v_0} = \sqrt {{v^2} - 2gh} }\)
Hướng dẫn giải
Ta có:
\(\begin{array}{l} h = \frac{{g{t^2}}}{2} = \frac{{{{(gt)}^2}}}{{2g}} \Leftrightarrow {(gt)^2} = 2gh\\ {v^2} = v_0^2 + v_y^2 = v_0^2 + {(gt)^2} = v_0^2 + 2gh\\ \Rightarrow {v_0} = \sqrt {{v^2} - 2gh} = \sqrt {{{25}^2} - 2.10.20} = 15(m/s) \end{array}\)
Vậy, vật được ném ngang ở độ cao 20 m phải có vận tốc đầu là 15 (m/s).
Tham khảo thêm
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 13: Lực. Tổng hợp và phân tích lực
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 14: Định luật I Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 15: Định luật II Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 16: Định luật III Niu-tơn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 17: Lực hấp dẫn
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 19: Lực đàn hồi
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 20: Lực ma sát
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 21: Hệ quy chiếu có gia tốc. Lực quán tính
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 22: Lực hướng tâm và lực quán tính li tâm. Hiện tượng tăng, giảm, mất trọng lực
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 23: Bài tập về động lực học
- doc Giải bài tập SGK Vật lý 10 Nâng cao Bài 24: Chuyển động của hệ vật
- doc Giải bài tập SGK Vật lý 10 nâng cao Bài 25: Thực hành: Xác định hệ số ma sát
.PNG)

