Giải bài tập SGK Toán 7 Bài 4: Khi nào góc xOy + góc yOz= góc xOz?
Phần hướng dẫn giải bài tập SGK Khi nào góc xOy + góc yOz= góc xOz? sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập hai.
Mục lục nội dung

1. Giải bài 18 trang 82 SGK Toán 6 tập 2
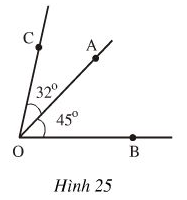
Hình 25 cho biết tia OA nằm giữa hai tia OB và OC, \(\widehat{BOA}= 45^{0}, \widehat{AOC}= 32^{0}\). Tính \(\widehat{BOC}\). Dùng thước đo góc để kểm tra lại.
Phương pháp giải
Nếu Oy nằm giữa hai tia Ox và Oz thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).
Hướng dẫn giải
Vì tia OA nằm giữa hai tia OB, OC nên
\(\widehat{BOC} =\widehat{BOA}+\widehat{AOC}=45^{0}+32^{0} =77^{0}\)
2. Giải bài 19 trang 82 SGK Toán 6 tập 2
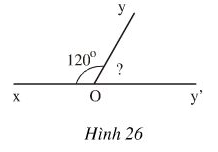
Hình 26 cho biết hai góc kề bù \(xOy\) và \(yOy',\) \(\widehat{xOy} = 120^{0}\) . Tính \(\widehat{yOy'}\)
Phương pháp giải
Chú ý: Hai góc kề bù là hai góc có tổng số đo bằng 180 độ
Hướng dẫn giải
Hai góc \(xOy\) và \(yOy'\) kề bù nên \(\widehat{xOy} +\widehat{yOy'}= 180^{0}\)
suy ra: \(\widehat{yOy'}= 180^{0} -\widehat{xOy}\)\( =180^{0}-120^{0}=60^{0}\)
3. Giải bài 20 trang 82 SGK Toán 6 tập 2
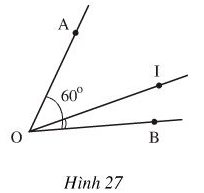
Hình 27 cho biết tia \(OI\) nằm giữa hai tia \(OA, OB,\) \(\widehat{AOB}= 60^{0}, \widehat{BOI}= \dfrac{1}{4}\widehat{ AOB}\). Tính số đo góc \(BOI\) và \(AOI.\)
Phương pháp giải
Nếu \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).
Hướng dẫn giải
Ta có \(\widehat{BOI}= \dfrac{1}{4}\widehat{ AOB}=\dfrac{1}{4}.60^{0}=15^{0}\)
Do tia \(OI\) nằm giữa hai tia \(OA, OB\) nên \(\widehat{AOI}+\widehat{ BOI}=\widehat{AOB}\)
Suy ra \(\widehat{AOI} + 15^{0}= 60^{0}\) hay \(\widehat{AOI}= 60^{0}- 15^{0}=45^{0}\)
4. Giải bài 21 trang 82 SGK Toán 6 tập 2
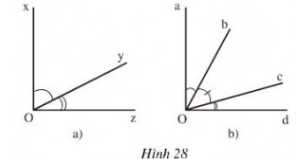
a) Đo các góc ở hình 28 a,b.
b) Viết tên các cặp góc phụ nhau ở hình 28b.
Phương pháp giải
Hai góc phụ nhau là hai góc có tổng số đo bằng 90 độ.
Hướng dẫn giải
Câu a
Hình a: \(\widehat{xOy}= 63^{0};\widehat{yOz}= 27^{0}\) ;\(\widehat{xOz}= 90^{0} \)
Hình b: \(\widehat{aOb}= 30^{0};\) \(\widehat{bOc }= 45^{0}; \widehat{cOd}= 15^{0}; \widehat{aOc }= 75^{0};\)
\(\widehat{bOd}= 60^{0};\widehat{aOd}=90^{0}\);
Câu b
Các cặp góc phụ nhau ở hình 28b là:
\(\widehat{aOb }\) và \(\widehat{bOd}\) (vì \(\widehat{aOb }+\widehat{bOd}=30^0+60^0=90^{0})\)
\(\widehat{aOc}\) và \(\widehat{cOd}\) (vì \(\widehat{aOc}+\widehat{cOd}=75^0+15^0= 90^{0})\)
5. Giải bài 22 trang 82 SGK Toán 6 tập 2
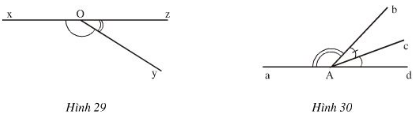
a) Đo các góc ở hình 29,30.
b) Viết tên các góc bù nhau ở hình 30.
Phương pháp giải
Hai góc bù nhau là hai góc có tổng số đo bằng 180 độ.
Hướng dẫn giải
Câu a
Hình 29 ta có: \(\widehat {xOy} = {147^0};\widehat {yOz} = {33^0};\widehat {xOz} = {180^0}\)
Hình 30 ta có: \(\widehat{aAb}=133^{0}; \widehat{bAc}= 27^{0};\widehat{cAd}=20^{0}\)
\(\widehat{aAc}=160^{0}; \widehat{bAd}= 47^{0};\widehat{aAd}=180^{0}\).
Câu b
Các cặp góc bù nhau ở hình 30 là:
\(\widehat{aAb}, \widehat{bAd}\) ( vì \(\widehat{aAb} + \widehat{bAd}\) \(= 133^0 + 47^0 = 180^0 \))
\(\widehat{aAc}, \widehat{cAd}\) (vì \(\widehat{aAc}+ \widehat{cAd}\) \(=160^0+20^0=180^0\))
6. Giải bài 23 trang 82 SGK Toán 6 tập 2
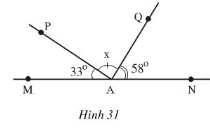
Hình 31 cho biết hai tia \(AM\) và \(AN\) đối nhau,\(\widehat{MAP}= 33^{0} , \widehat{NAQ}= 58^{0},\) tia \(AQ\) nằm giữa hai tia \(AN\) và \(AP .\) Hãy tính số đo \(x\) của \(\widehat{PAQ}\)
Phương pháp giải
Nếu \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).
Hai góc kề bù thì có tổng số đo bằng \(180\) độ.
Hướng dẫn giải
Vì \(AM\) và \(AN\) là hai tia đối nhau nên \(\widehat{MAP}\) và \(\widehat{PAN}\) là hai góc kề bù.
Do đó, \(\widehat{MAP}+\widehat{PAN}=180^0\)
Suy ra \(\widehat{PAN}=180^0-\widehat{MAP}\)\(={180^0} - {33^0} = {147^0}\)
Vì tia \(AQ\) nằm giữa hai tia \(AN\) và \(AP\)
Suy ra \(\widehat{PAN}=\widehat{PAQ}+\widehat{QAN}\)
Hay \(147^0= x + 58^0 \)
Nên \(x = 147^0-58^0=89^0\)
Vậy \(\widehat{PAQ}=89^0\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Nửa mặt phẳng
- doc Giải bài tập SGK Toán 7 Bài 2: Góc
- doc Giải bài tập SGK Toán 7 Bài 2: Số đo góc
- doc Giải bài tập SGK Toán 7 Bài 5: Vẽ góc cho biết số đo
- doc Giải bài tập SGK Toán 7 Bài 6: Tia phân giác của góc
- doc Giải bài tập SGK Toán 6 Bài 8: Đường tròn
- doc Giải bài tập SGK Toán 6 Bài 9: Tam giác
- doc Giải bài tập SGK Toán 6 Ôn tập phần Hình học