Giải bài tập SGK Toán 6 Bài 16: Tìm tỉ số của hai số
Phần hướng dẫn giải bài tập SGK Tìm tỉ số của hai số sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập hai.
Mục lục nội dung
1. Giải bài 137 trang 57 SGK Toán 6 tập 2
2. Giải bài 138 trang 58 SGK Toán 6 tập 2
3. Giải bài 139 trang 58 SGK Toán 6 tập 2
4. Giải bài 140 trang 58 SGK Toán 6 tập 2
5. Giải bài 141 trang 58 SGK Toán 6 tập 2
6. Giải bài 142 trang 59 SGK Toán 6 tập 2
7. Giải bài 143 trang 59 SGK Toán 6 tập 2
8. Giải bài 144 trang 59 SGK Toán 6 tập 2
9. Giải bài 145 trang 59 SGK Toán 6 tập 2
10. Giải bài 146 trang 59 SGK Toán 6 tập 2

1. Giải bài 137 trang 57 SGK Toán 6 tập 2
Tìm tỉ số của:
a) \(\dfrac{2}{3}\)m và 75cm ; b) \(\dfrac{3}{10}\)h và 20 phút.
Phương pháp giải
Thương trong phép chia số a cho số b (b khác 0) gọi là tỉ số của a và b.
Tỉ số của a và b kí hiệu là a: b (cũng kí hiệu là \(\dfrac{a}{b}\) ).
Khái niệm tỉ số thường được dùng khi nói về thương của hai đại lượng (cùng loại và cùng đơn vị đo).
Hướng dẫn giải
Đưa hai số về cùng đơn vị đo.
Câu a
\( \displaystyle 75cm = {{75} \over {100}}m = {3 \over 4}m\) , do đó tỉ số của \( \displaystyle \dfrac{2}{3}\)m và 75cm là:
\( \displaystyle {2 \over 3}:{3 \over 4} = {2 \over 3}.{4 \over 3} = {8 \over 9}\)
Câu b
Ta có: \( \displaystyle \dfrac{3}{10}\)h = \( \displaystyle {3 \over {10}}.60\) phút = 18 phút
Suy ra: Tỉ số của \( \displaystyle \dfrac{3}{10}\)h và 20 phút là: \( \displaystyle 18:20 = {{18} \over {20}} = {9 \over {10}}\)
Chú ý:
Câu a) ta có thể cùng đổi ra đơn vị là cm rồi tính tỉ số
Câu b) ta có thể cùng đổi ra đơn vị là giờ rồi tính tỉ số
2. Giải bài 138 trang 58 SGK Toán 6 tập 2
Ta có thể đưa tỉ số của hai số về tỉ số của hai số nguyên.
Chẳng hạn, tỉ số của hai số 0,75 và \(1\dfrac{7}{20}\) có thể viết như sau:
\(\dfrac{0,75}{1\dfrac{7}{20}}=\dfrac{\dfrac{75}{100}}{\dfrac{27}{20}}=\dfrac{75}{100}.\dfrac{20}{27}=\dfrac{5}{9}.\)
Hãy viết các tỉ số sau đây thành tỉ số của hai số nguyên:
a) \(\dfrac{1,28}{3,15}\) ; b) \(\dfrac{2}{5}:3\dfrac{1}{4}\) ;
c) \(1\dfrac{3}{7}:1,24\) ; d) \(\dfrac{2\tfrac{1}{5}}{3\tfrac{1}{7}}\).
Phương pháp giải
Đưa các số thập phân, các hỗn số về dạng phân số rồi tính toán.
Hướng dẫn giải
Câu a
\(\dfrac{{1,28}}{{3,15}} = \dfrac{{\dfrac{{128}}{{100}}}}{{\dfrac{{315}}{{100}}}} = \dfrac{{128}}{{100}}.\dfrac{{100}}{{315}} = \dfrac{{128}}{{315}}\)
Câu b
\(\dfrac{2}{5}:3\dfrac{1}{4} = \dfrac{2}{5}:\dfrac{{13}}{4} = \dfrac{2}{5}.\dfrac{4}{{13}} = \dfrac{8}{{65}}\)
Câu c
\(1\dfrac{3}{7}:1,24 = \dfrac{{10}}{7}:\dfrac{{124}}{{100}} \)\(= \dfrac{{10}}{7}.\dfrac{{100}}{{124}} = \dfrac{{250}}{{217}}\)
Câu d
\(\dfrac{{2\dfrac{1}{5}}}{{3\dfrac{1}{7}}} = \dfrac{{\dfrac{{11}}{5}}}{{\dfrac{{22}}{7}}} = \dfrac{{11}}{5}.\dfrac{7}{{22}} = \dfrac{7}{{10}}\)
3. Giải bài 139 trang 58 SGK Toán 6 tập 2
Tỉ số của hai số a và b có thể viết là \(\dfrac{a}{b}\). Cách viết này có khác gì cách viết phân số \(\dfrac{a}{b}\) không ? Cho ví dụ.
Phương pháp giải
Xem lại khái niệm phân số
Hướng dẫn giải
Cách viết phân số \(\dfrac{a}{b}\) khác cách viết tỉ số \(\dfrac{a}{b}\) ở chỗ trong phân số \(\dfrac{a}{b}\) thì a và b bắt buộc phải là các số nguyên còn trong tỉ số \(\dfrac{a}{b}\) thì a và b là những số bất kì, với b ≠ 0.
Ví dụ: \(\dfrac{-3}{5}\) là phân số (cũng là tỉ số); \(\dfrac{0,72}{3\dfrac{1}{4}}\) là tỉ số nhưng không là phân số.
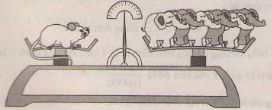
4. Giải bài 140 trang 58 SGK Toán 6 tập 2
Chuột nặng hơn voi !
Một con chuột nặng 30g còn một con voi nặng 5 tấn. Tỉ số giữa khối lượng của một con chuột và khối lượng của một con voi là \(\dfrac{30}{5}=6\) , nghĩa là một con chuột nặng bằng 6 con voi ! Em có tin như vậy không ? Sai lầm ở chỗ nào ?
Phương pháp giải
Tỉ số của hai số a và b được viết là \(\dfrac{a}{b}\) hoặc \(a : b.\)
Lưu ý: \(a,b\) cùng đơn vị đo.
Hướng dẫn giải
Em không tin như vậy.
Sai lầm ở chỗ đã dùng các số đo bởi hai đơn vị đo khác nhau để tính tỉ lệ. Cần đưa về một số đo mới có tỉ lệ chính xác. Ví dụ đổi 5 tấn ra gam hoặc ngược lại đổi 30 gam ra tấn, rồi mới lập tỉ số.
Đổi 5 tấn = 5000000 gam
Tỉ số giữa các khối lượng chuột và voi tính theo đơn vị bằng gam là : \(\dfrac{30}{5000000}=\dfrac{3}{500000}\).
5. Giải bài 141 trang 58 SGK Toán 6 tập 2
Tỉ số của hai số a và b bằng \(1\dfrac{1}{2}\) . Tìm hai số đó biết \(a - b = 8\)
Phương pháp giải
Thương trong phép chia số a cho số b (b khác 0) gọi là tỉ số của a và b.
Tỉ số của a và b kí hiệu là \(a: b\) (cũng kí hiệu là \(\dfrac{a}{b}\) ).
Hướng dẫn giải
Đổi \(1\dfrac{1}{2} = \dfrac{3}{2}\)
Vì tỉ số của a và b bằng \(1\dfrac{1}{2}=\dfrac{3}{2}\) nên \(\dfrac{a}{b} = \dfrac{3}{2}\) suy ra \(a = \dfrac{{3}}{2}.b\).
Lại có \(a - b = 8\) nên thay \(a = \dfrac{{3}}{2}.b\) ta được:
\(\dfrac{{3}}{2}.b - b = 8\)
\(b.(\dfrac{{3}}{2}-1)=8\)
\(\dfrac{1}{2}.b = 8\)
\(b=8:\dfrac{1}{2}\)
\(b=16\)
Do đó \(b = 16\) và \(a = \dfrac{{3}}{2}.16 = 24\)
6. Giải bài 142 trang 59 SGK Toán 6 tập 2
Khi nói đến vàng ba số 9 (999) ta hiểu rằng: Trong 1000g “vàng” này chứa tới 999g vàng nguyên chất , nghĩa là tỉ lệ vàng nguyên chất là \(\displaystyle {{999} \over {1000}} = 99,9\%\)
Em hiểu thế nào khi nói đến vàng bốn số 9 (9999)?
Phương pháp giải
Muốn tìm tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu phần trăm vào kết quả \(\dfrac{{a.100}}{b}\,\,\% \)
Hướng dẫn giải
Nói vàng bốn số 9 có nghĩa là trong \(10 000g\) "vàng" này chứa tới \(9999g\) vàng nguyên chất, nghĩa là tỉ lệ vàng nguyên chất là \(\displaystyle {{9999} \over {10000}} = 99,99\%\) (tỉ lệ này cao hơn vàng 3 số 9)
7. Giải bài 143 trang 59 SGK Toán 6 tập 2
Trong 40 kg nước biển có 2 kg muối. Tính tỉ số phần trăm muối trong nước biển.
Phương pháp giải
Muốn tìm tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào kết quả: \(\dfrac{{a.100}}{b}\% \)
Hướng dẫn giải
Tỉ số phần trăm muối có trong nước biển là: \(\displaystyle {{2.100} \over {40}}\% = 5\%\)
Vậy tỉ số phần trăm muối trong nước biển là 5%
8. Giải bài 144 trang 59 SGK Toán 6 tập 2
Biết tỉ số phần trăm nước trong dưa chuột là 97,2%. Tính lượng nước trong 4 kg dưa chuột.
Phương pháp giải
Muốn tìm \(\dfrac{m}{n}\) của số \(b\) cho trước, ta tính \(b.\dfrac{m}{n}\) với \((m,n\in N, n\ne 0)\)
Hướng dẫn giải
Lượng nước trong 4kg dưa chuột là:
\(\displaystyle 97,2\% .4 = {{97,2} \over {100}}.4 = 3,888\) (kg)
Vậy lượng nước trong 4kg dưa chuột là 3,888kg.
9. Giải bài 145 trang 59 SGK Toán 6 tập 2
Tìm tỉ lệ xích của một bản đồ, biết rằng quãng đường từ Hà Nội đến Thái Nguyên trên bản đồ là 4 cm còn trong thực tế là 80 km.
Phương pháp giải
Tỉ lệ xích = bản đồ : thực tế
T = a/b
Hướng dẫn giải
Ta có:
Tỉ lệ xích = bản đồ : thực tế
Đổi ra cm: 80km = 8 000 000 cm
Tỉ lệ xích của bản đồ là:
\( \displaystyle T = {4 \over {8000000}} = {1 \over {2000000}}\)
10. Giải bài 146 trang 59 SGK Toán 6 tập 2
Trên một bản vẽ kĩ thuật có tỉ lệ xích 1:125, chiều dài của một chiếc máy bay Bô – inh (Boeing) 747 là 56,408 cm. Tính chiều dài thật của chiếc máy bay đó.
Phương pháp giải
Sử dụng tỉ lệ xích \(T=\dfrac{a}{b}\), từ đó tìm được chiều dài thật của máy bay.
Hướng dẫn giải
Gọi a (cm) là chiều dài thật của máy bay.
Theo đề bài ta có tỉ lệ xích \(T=1:125=\dfrac{1}{125}\)
Do đó:
\(\displaystyle T = {1 \over {125}}= {{56,408} \over a} \)
\(\displaystyle \Rightarrow a = 56,408.125 \)\(= 7051(cm)=70,51(m)\)
Vậy chiều dài thật của máy bay Bo-inh là 70,51 m
11. Giải bài 147 trang 69 SGK Toán 6 tập 2
Cầu Mỹ Thuận (h.12) nối hai đỉnh Tiền Giang và Vĩnh Long được khánh thành ngày 21-5-2000.
Cầu Mỹ Thuận là cây cầu treo hiện đại (cầu dây văng) đầu tiền ở nước ta với chiều dài 1535 m bắc ngang sông Tiền, một trong những con sông rộng nhất Việt Nam. Nếu vẽ trên bản đồ tỉ lệ xích 1 : 20000 thì cây cầu này dài bao nhiêu xentimet?
Phương pháp giải
Tỉ lệ xích \(T=\dfrac{a}{b}\) với \(a,b\) lần lượt là chiều dài trên bản đồ và trên thực tế.
Hướng dẫn giải
Đổi \(1535m=153500cm\)
Gọi b (cm) là chiều dài cầu Mỹ Thuận trên bản đồ.
Vì tỉ lệ xích trên bản đồ là \(1:20000\) nên ta có
\(T = \dfrac{1}{{20000}} = \dfrac{b}{{153500}}\)
Suy ra \(20000b = 153500 \Rightarrow b = \dfrac{{153500}}{{20000}} = 7,675cm\)
Do đó, chiều dài cây cầu trên bản đồ bằng 7,675 cm.
12. Giải bài 147 trang 60 SGK Toán 6 tập 2
Sử dụng máy tính bỏ túi
Dùng máy tính bỏ túi để tính tỉ số phần trăm của:
a) 65 và 160
b) 0,453195 và 0,15;
c) 1762384 và 4405960.
Phương pháp giải
Muốn tìm tỉ số phần trăm của hai số a và b, ta nhân a với 100 rồi chia cho b và viết kí hiệu % vào kết quả:
\(\dfrac{{a.100}}{b}\% \)
Hướng dẫn giải
Sử dụng máy tính bỏ túi và làm theo hướng dẫn trên, ta được kết quả:
a) \(\dfrac{{65}}{{160}}.100\% = 40,625\% \)
b) \(\dfrac{{0,453195}}{{0,15}}.100\% =302,13\%\)
c) \(\dfrac{{1762384}}{{4405960}}.100\% =40\%\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Mở rộng khái niệm về phân số
- doc Giải bài tập SGK Toán 6 Bài 2: Phân số bằng nhau
- doc Giải bài tập SGK Toán 6 Bài 3: Tính chất cơ bản của phân số
- doc Giải bài tập SGK Toán 6 Bài 4: Rút gọn phân số
- doc Giải bài tập SGK Toán 6 Bài 5: Quy đồng mẫu số nhiều phân số
- doc Giải bài tập SGK Toán 6 Bài 6: So sánh phân số
- doc Giải bài tập SGK Toán 6 Bài 7: Phép cộng phân số
- doc Giải bài tập SGK Toán 6 Bài 8: Tính chất cơ bản của phép cộng phân số
- doc Giải bài tập SGK Toán 6 Bài 9: Phép trừ phân số
- doc Giải bài tập SGK Toán 6 Bài 10: Phép nhân phân số
- doc Giải bài tập SGK Toán 6 Bài 11: Tính chất cơ bản của phép nhân phân số
- doc Giải bài tập SGK Toán 6 Bài 12: Phép chia phân số
- doc Giải bài tập SGK Toán 6 Bài 13: Hỗn số. Số thập phân. Phần trăm
- doc Giải bài tập SGK Toán 6 Bài 14: Tìm giá trị phân số của một số cho trước
- doc Giải bài tập SGK Toán 6 Bài 15: Tìm một số biết giá trị một phân số của nó
- doc Giải bài tập SGK Toán 6 Bài 17: Biểu đồ phần trăm
- doc Giải bài tập SGK Toán 6 Ôn tập Chương 3: Phân số
- doc Giải bài tập SGK Toán 6 Ôn tập cuối năm