Giải bài tập SGK Toán 6 Bài 8: Tính chất cơ bản của phép cộng phân số

Tính nhanh.

a) \(\dfrac{-3}{7}+\dfrac{5}{13}+\dfrac{-4}{7}\) ; 

b) \(\dfrac{-5}{21}+\dfrac{-2}{21}+\dfrac{8}{24}\) .

Phương pháp giải

Sử dụng các tính chất sau đây:

• Tính chất giao hoán: \(\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{c}{d}+\dfrac{b}{a}.\)
• Tính chất kết hợp: \(\left (\dfrac{a}{b}+\dfrac{c}{d} \right )+ \dfrac{p}{q}=\dfrac{a}{b}+\left (\dfrac{c}{d}+\dfrac{p}{q} \right ).\)

Hướng dẫn giải

Câu a:

\(\dfrac{{ - 3}}{7} + \dfrac{5}{{13}} + \dfrac{{ - 4}}{7} \)

\(=  \left( \dfrac{{ - 3}}{7} + \dfrac{{ - 4}}{7} \right)+ \dfrac{5}{{13}}\)

\(= \dfrac{{ - 7}}{7} + \dfrac{5}{{13}} =  - 1 + \dfrac{5}{{13}}\)

\(=\dfrac{-13}{13}+\dfrac{5}{13}=\dfrac{-8}{13}\).

Câu b:

\(\eqalign{
& {{ - 5} \over {21}} + {{ - 2} \over {21}} + {8 \over {24}} \cr
& = \left( {{{ - 5} \over {21}} + {{ - 2} \over {21}}} \right) + {8 \over {24}} \cr
& = {{ - 7} \over {21}} + {8 \over {24}} \cr
& = {{ - 1} \over 3} + {1 \over 3} = 0 \cr} \)

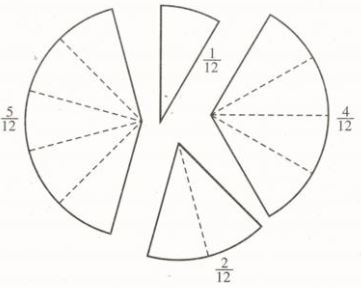
Đố: Cắt một tấm bìa hình tròn bán kính 2,5cm thành 4 phần không bằng nhau như hình 8.

Đố em đặt các miếng bìa đã cắt cạnh nhau để được:

a) \(\dfrac{1}{4}\) hình tròn;

b) \(\dfrac{1}{2}\) hình tròn; 

c) \(\dfrac{7}{12},\dfrac{2}{3},\dfrac{3}{4},\dfrac{5}{6},\dfrac{11}{12}\) và \(\dfrac{12}{12}\) hình tròn.

Phương pháp giải

Ghép các phần sao cho tổng của chúng bằng phân số cần tìm.

Hướng dẫn giải

Ghép các miếng bìa như sau:

Câu a:

Ta đặt hai miếng bìa \(\dfrac{1}{12}\) và \(\dfrac{2}{12}\) cạnh nhau để được \(\dfrac{1}{4}\) hình tròn.

Vì \(\dfrac{1}{12}+\dfrac{2}{12}=\dfrac{3}{12}=\dfrac{1}{4}.\) 

Câu b:

Ta đặt hai miếng bìa \(\dfrac{1}{12}\) và \(\dfrac{5}{12}\) cạnh nhau để được \(\dfrac{1}{2}\) hình tròn.

Vì \(\dfrac{1}{12}+\dfrac{5}{12}=\dfrac{6}{12}=\dfrac{1}{2}.\)

Hoặc ta đặt hai miếng bìa \(\dfrac{4}{12}\) và \(\dfrac{2}{12}\) cạnh nhau để được \(\dfrac{1}{2}\) hình tròn.

Vì \(\dfrac{4}{12}+\dfrac{2}{12}=\dfrac{6}{12}=\dfrac{1}{2}.\)

Câu c:

Tương tự, từ các phép tính dưới đây ta sẽ suy ra các miếng bìa đặt cạnh nhau để thỏa mãn đề bài.

\(\dfrac{5}{12}+\dfrac{2}{12}=\dfrac{7}{12};\)                         

\(\dfrac{5}{12}+\dfrac{2}{12}+\dfrac{1}{12}=\dfrac{8}{12}=\dfrac{2}{3};\)

\(\dfrac{5}{12}+\dfrac{4}{12}=\dfrac{9}{12}=\dfrac{3}{4};\)                

\(\dfrac{5}{12}+\dfrac{4}{12}+\dfrac{1}{12}=\dfrac{10}{12}=\dfrac{5}{6};\)

\(\dfrac{5}{12}+\dfrac{4}{12}+\dfrac{2}{12}=\dfrac{11}{12};\)               

\(\dfrac{5}{12}+\dfrac{4}{12}+\dfrac{2}{12}+\dfrac{1}{12}=\dfrac{12}{12}.\) 

Hùng đi xe đạp, 10 phút đầu đi được \(\dfrac{1}{3}\) quãng đường, 10 phút thứ hai đi được \(\dfrac{1}{4}\) quãng đường, 10 phút cuối cùng đi được \(\dfrac{2}{9}\) quãng đường. Hỏi sau 30 phút Hùng đi được bao nhiêu phần quãng đường ?

Phương pháp giải

Cộng các phân số với nhau ta sẽ ra được số phần quãng đường.

Hướng dẫn giải

Sau 30 phút Hùng đi được số phần quãng đường là:

\(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{2}{9}\)\(=\dfrac{{12}}{{36}} + \dfrac{9}{{36}} + \dfrac{8}{{36}} \)\(= \dfrac{{12 + 9 + 8}}{{36}} = \dfrac{29}{36}\) (quãng đường).

Vậy sau 30 phút Hùng đi được \(\displaystyle {{29} \over {36}}\) (quãng đường). 

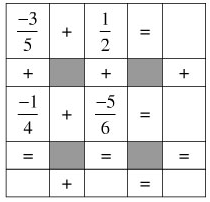
Điền số thích hợp vào ô trống ở bảng dưới:

Phương pháp giải

Thực hiện phép tính cộng theo từng hàng và từng cột.

Hướng dẫn giải

Cụ thể, ta có: 

\(\dfrac{{ - 3}}{5} + \dfrac{1}{2} = \dfrac{{ - 6}}{{10}} + \dfrac{5}{{10}} \)\(= \dfrac{{ - 6 + 5}}{{10}} = \dfrac{{ - 1}}{{10}}\)

\(\dfrac{{ - 1}}{4} + \dfrac{{ - 5}}{6} = \dfrac{{ - 3}}{{12}} + \dfrac{{ - 10}}{{12}}  \)\(= \dfrac{{ - 3 +(- 10)}}{{12}} = \dfrac{{ - 13}}{{12}}\)

\(\dfrac{{ - 3}}{5} + \dfrac{{ - 1}}{4} = \dfrac{{ - 12}}{{20}} + \dfrac{{ - 5}}{{20}}  \)\(= \dfrac{{ - 12 +(- 5)}}{{20}} = \dfrac{{ - 17}}{{20}}\) 

\(\dfrac{1}{2} + \dfrac{{ - 5}}{6} = \dfrac{3}{6} + \dfrac{{ - 5}}{6} = \dfrac{{3+( - 5)}}{6}  \)\(= \dfrac{{ - 2}}{6} = \dfrac{{ - 1}}{3}\) 

\(\dfrac{{ - 1}}{{10}} + \dfrac{{ - 13}}{{12}} = \dfrac{{ - 6}}{{60}} + \dfrac{{ - 65}}{{60}}  \)\(= \dfrac{{ - 6 +(- 65)}}{{60}} = \dfrac{{ - 71}}{{60}}\)

\(\dfrac{{ - 17}}{{20}} + \dfrac{{ - 1}}{3} = \dfrac{{ - 51}}{{60}} + \dfrac{{ - 20}}{{60}} \)\(= \dfrac{{ - 51 + \left( { - 20} \right)}}{{60}} = \dfrac{{ - 71}}{{60}}\)

Tìm năm cách chọn ba trong bảy số sau đây để khi cộng lại được tổng là 0:

\(\dfrac{-1}{6},\dfrac{-1}{3},\dfrac{-1}{2},0, \dfrac{1}{2},\dfrac{1}{3};\dfrac{1}{6}.\)

Ví dụ:\(\dfrac{-1}{2}+\dfrac{1}{3}+\dfrac{1}{6}=0.\) 

Phương pháp giải

Chọn ra các phân số mà có tổng là 0.

Lưu ý rằng: Phân số nào cộng với 0 cũng bằng chính nó.

Hướng dẫn giải

Cách 1: \(\dfrac{-1}{6}+0+\dfrac{1}{6}=0\) 

Cách 2: \(\dfrac{-1}{3}+0+\dfrac{1}{3}=0\) 

Cách 3: \(\dfrac{-1}{2}+0+\dfrac{1}{2}=0\)  

Cách 4: \(\dfrac{-1}{6}+\dfrac{-1}{3}+\dfrac{1}{2}=0\) .

Cách 5: \(\dfrac{1}{6} + \dfrac{1}{3} + \dfrac{{ - 1}}{2}=0 \) 

Điền số thích hợp vào ô trống: 

Phương pháp giải

- Tìm a + b: Muốn tìm tổng ta lấy số hạng cộng với số hạng:

• Muốn cộng hai phân số cùng mẫu ta cộng các tử và giữ nguyên mẫu.
• Muốn cộng hai phân số khác mẫu ta viết chúng dưới dạng hai phân số có cùng mẫu rồi cộng các tử và giữ nguyên mẫu chung.

- Tìm a hoặc b: Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.

Hướng dẫn giải

Giải thích: 

\(\displaystyle a + b = \dfrac{6}{{27}} + \dfrac{5}{{27}} = \dfrac{{11}}{{27}}\)

\(\displaystyle a + \dfrac{4}{{23}} = \dfrac{{11}}{{23}}\) nên \(\displaystyle a = \dfrac{7}{{23}}\) để \(\displaystyle \dfrac{7}{{23}} + \dfrac{4}{{23}} = \dfrac{{11}}{{23}}\)

\(\displaystyle a + b = \dfrac{3}{5} + \dfrac{7}{{10}} = \dfrac{6}{{10}} + \dfrac{7}{{10}} = \dfrac{{13}}{{10}}\)

\(\displaystyle a + b = \dfrac{5}{{14}} + \dfrac{2}{7} = \dfrac{5}{{14}} + \dfrac{4}{{14}} = \dfrac{9}{{14}}\)

\(\displaystyle a + b = \dfrac{4}{3} + \dfrac{2}{3} = \dfrac{6}{3} = 2\)

\(\displaystyle \dfrac{2}{5} + b = \dfrac{8}{5}\) nên \(\displaystyle b = \dfrac{6}{5}\) để \(\displaystyle \dfrac{2}{5} + \dfrac{6}{5} = \dfrac{8}{5}\) 

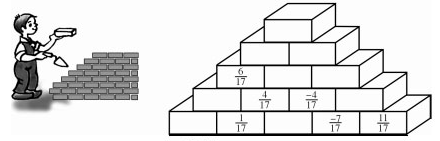
“Xây trường”

Em hãy “xây bức tường” ở hình 9 này bằng cách điền các phân số thích hợp vào các “viên gạch” theo quy tắc sau:

a = b + c (h.10).

Phương pháp giải

- Muốn cộng hai phân số cùng mẫu dương ta cộng các tử số và giữ nguyên mẫu số.

- Hai phân số đối nhau có tổng bằng 0.

- Phân số nào cộng với 0 cũng bằng chính phân số đó.

Hướng dẫn giải

Làm theo quy tắc ở hình 10, ta có thể "xây tường" như sau:

Trong vở bài tập của bạn An có bài làm sau:

a) \( \displaystyle {{ - 3} \over 5} + {1 \over 5} = {4 \over 5}\)  

b) \( \displaystyle {{ - 10} \over {13}} + {{ - 2} \over {13}} = {{ - 12} \over {13}}\)

c) \( \displaystyle {2 \over 3} + {{ - 1} \over 6} = {4 \over 6} + {{ - 1} \over 6} = {3 \over 6} = {1 \over 2}\)

d) \( \displaystyle {{ - 2} \over 3} + {2 \over { - 5}} = {{ - 2} \over 3} + {{ - 2} \over 5} \)\( \displaystyle = {{ - 10} \over {15}} + {{ - 6} \over {15}} = {{ - 4} \over {15}}\)

Hãy kiểm tra lại các đáp số và sửa lại chỗ sai (nếu có).

Phương pháp giải

- Muốn cộng hai phân số cùng mẫu ta cộng các tử và giữ nguyên mẫu.

- Muốn cộng hai phân số khác mẫu ta viết chúng dưới dạng hai phân số có cùng mẫu rồi cộng các tử và giữ nguyên mẫu chung. 

Hướng dẫn giải

Câu b và câu c bạn An làm đúng.

Lỗi sai ở câu a) và câu d). Sửa lại như sau

a) \(\displaystyle {{ - 3} \over 5} + {1 \over 5} = {{ - 2} \over 5}\)

d) \(\displaystyle {{ - 2} \over 3} + {2 \over { - 5}} = {{ - 2} \over 3} + {{ - 2} \over 5}\)\(\displaystyle = {{ - 10} \over {15}} + {{ - 6} \over {15}} = {{ - 16} \over {15}}\)  

Điền số thích hợp vào ô trống. Chú ý rút gọn kết quả (nếu có thể):

Phương pháp giải

- Muốn cộng hai phân số cùng mẫu ta cộng các tử và giữ nguyên mẫu.

- Muốn cộng hai phân số khác mẫu ta viết chúng dưới dạng hai phân số có cùng mẫu rồi cộng các tử và giữ nguyên mẫu chung. 

Hướng dẫn giải

Giải thích:  

Trước hết ta tính các kết quả ở “đường chéo chính” của ô vuông.

\(\begin{array}{l}\dfrac{5}{9} + \dfrac{5}{9} = \dfrac{{10}}{9}\\\dfrac{1}{{36}} + \dfrac{1}{{36}} = \dfrac{2}{{36}} = \dfrac{1}{{18}}\\\dfrac{{ - 11}}{{18}} + \dfrac{{ - 11}}{{18}} = \dfrac{{ - 22}}{{18}} = \dfrac{{ - 11}}{9}\end{array}\)

Tiếp đó, ta tính các kết quả ở “đường chéo phụ” :

\(\begin{array}{l}\dfrac{5}{9} + \dfrac{{ - 1}}{2} = \dfrac{{5.2 + \left( { - 1} \right).9}}{{18}}\\ = \dfrac{{10 + \left( { - 9} \right)}}{{18}} = \dfrac{1}{{18}}\\\dfrac{1}{{36}} + \dfrac{5}{9} = \dfrac{{1 + 5.4}}{{36}} = \dfrac{{1 + 20}}{{36}}\\ = \dfrac{{21}}{{36}} = \dfrac{7}{12}\\\dfrac{{ - 11}}{{18}} + \dfrac{1}{{36}} = \dfrac{{ - 11.2 + 1}}{{36}}\\ = \dfrac{{ - 22 + 1}}{{36}} = \dfrac{{ - 21}}{{36}} = \dfrac{{ - 7}}{{12}}\\\dfrac{1}{{36}} + \dfrac{{ - 1}}{2} = \dfrac{{1 + \left( { - 1} \right).18}}{{36}} \\= \dfrac{{1 + \left( { - 18} \right)}}{{36}} = \dfrac{{ - 17}}{{36}}\\\dfrac{{ - 11}}{{18}} + \dfrac{5}{9} = \dfrac{{ - 11 + 5.2}}{{18}} \\= \dfrac{{ - 11 + 10}}{{18}} = \dfrac{{ - 1}}{{18}}\\\dfrac{{ - 11}}{{18}} + \dfrac{{ - 1}}{2} = \dfrac{{ - 11 + \left( { - 1} \right).9}}{{18}}\\ = \dfrac{{ - 11 + \left( { - 9} \right)}}{{18}} = \dfrac{{ - 20}}{{18}} = \dfrac{{ - 10}}{9}\end{array}\)

Do tính chất giao hoán của phép cộng phân số ta có ngay các kết quả :

\(\begin{array}{l}\dfrac{{ - 1}}{2} + \dfrac{5}{9} = \dfrac{5}{9} + \dfrac{{ - 1}}{2} = \dfrac{1}{{18}};\\\dfrac{5}{9} + \dfrac{1}{{36}} = \dfrac{1}{{36}} + \dfrac{5}{9} = \dfrac{7}{12};\\\dfrac{1}{{36}} + \dfrac{{ - 11}}{{18}} = \dfrac{{ - 11}}{{18}} + \dfrac{1}{{36}} = \dfrac{{ - 7}}{{12}};\\\dfrac{{ - 1}}{2} + \dfrac{1}{{36}} = \dfrac{1}{{36}} + \dfrac{{ - 1}}{2} = \dfrac{{ - 17}}{{36}};\\\dfrac{5}{9} + \dfrac{{ - 11}}{{18}} = \dfrac{{ - 11}}{{18}} + \dfrac{5}{9} = \dfrac{{ - 1}}{{18}};\\\dfrac{{ - 1}}{2} + \dfrac{{ - 11}}{{18}} = \dfrac{{ - 11}}{{18}} + \dfrac{{ - 1}}{2} = \dfrac{{ - 10}}{9}.\end{array}\)

Ta điền các kết quả tìm được vào bảng đã cho.

Lưu ý. Việc áp dụng tính chất giao hoán của phép cộng phân số \(\dfrac{a}{b} + \dfrac{c}{d} = \dfrac{c}{d} + \dfrac{a}{b}\) đã giúp cho việc tính toán được thuận tiện và nhanh chóng.

Tính nhanh giá trị của các biểu thức sau:

\( \displaystyle A = {{ - 5} \over {11}} + \left( {{{ - 6} \over {11}} + 1} \right)\)

\( \displaystyle B = {2 \over 3} + \left( {{5 \over 7} + {{ - 2} \over 3}} \right)\)

\( \displaystyle C = \left( {{{ - 1} \over 4} + {5 \over 8}} \right) + {{ - 3} \over 8}\) 

Phương pháp giải

- Phá ngoặc sau đó ta nhóm các phân số đối nhau hoặc cùng mẫu lại với nhau.

- Muốn cộng hai phân số có cùng mẫu dương ta cộng các tử số và giữ nguyên mẫu số. 

Hướng dẫn giải

\(\displaystyle A = {{ - 5} \over {11}} + \left( {{{ - 6} \over {11}} + 1} \right)\)

\(\displaystyle =\left( {{{ - 5} \over {11}} + {{ - 6} \over {11}}} \right) + 1 \)

\(\displaystyle = {{ - 11} \over {11}} + 1 =  - 1 + 1 = 0\)

\(\displaystyle B ={2 \over 3} + \left( {{5 \over 7} + {{ - 2} \over 3}} \right)\)

\(\displaystyle = \left( {{2 \over 3} + {{ - 2} \over 3}} \right) + {5 \over 7} \)

\(\displaystyle = 0 + {5 \over 7} = {5 \over 7}\)

\(\displaystyle C = \left( {{{ - 1} \over 4} + {5 \over 8}} \right) + {{ - 3} \over 8}\)

\(\displaystyle = {{ - 1} \over 4} + \left( {{5 \over 8} + {{ - 3} \over 8}} \right) \)

\(\displaystyle = {{ - 1} \over 4} + {2 \over 8}= {{ - 1} \over 4} + {1 \over 4} = 0\) 

Trong các câu sau đây, hãy chọn một câu đúng:

Muốn cộng hai phân số \( \displaystyle {{ - 3} \over 4}\) và \( \displaystyle {4 \over 5}\) ta làm như sau:

a) Cộng tử với tử, cộng mẫu với mẫu.

b) Nhận mẫu của phân số \( \displaystyle {{ - 3} \over 4}\) với 5, nhân mẫu của phân số \( \displaystyle {4 \over 5}\) với 4 rồi cộng hai tử lại.

c) Nhân cả tử lẫn mẫu của phân số \( \displaystyle {{ - 3} \over 4}\) với 5, nhân cả tử lẫn mẫu của phân số \( \displaystyle {4 \over 5}\) với 4 rồi cộng hai tử mới lại , giữ nguyên mẫu chung.

d) Nhân cả tử lẫn mẫu của phân số \( \displaystyle {{ - 3} \over 4}\) với 5, nhân cả tử lẫn mẫu của phân số \( \displaystyle {4 \over 5}\) với 4 rồi cộng tử với tử, mẫu với mẫu.

Phương pháp giải

- Muốn cộng hai phân số cùng mẫu ta cộng các tử và giữ nguyên mẫu.

- Muốn cộng hai phân số khác mẫu ta viết chúng dưới dạng hai phân số có cùng mẫu rồi cộng các tử và giữ nguyên mẫu chung. 

Hướng dẫn giải

Phép tính đúng: \(\dfrac{{ - 3}}{4} + \dfrac{4}{5} = \dfrac{{ - 15}}{{20}} + \dfrac{{16}}{{20}} \)

\(= \dfrac{{ - 15 + 16}}{{20}} = \dfrac{1}{{20}}\)

Ở phép tính trên ta đã: Nhân cả tử lẫn mẫu của phân số \(\displaystyle {{ - 3} \over 4}\) với 5, nhân cả tử lẫn mẫu của phân số \(\displaystyle {4 \over 5}\) với 4 rồi cộng hai tử mới lại , giữ nguyên mẫu chung.

Như vậy, ta thấy chỉ có đáp án C đúng.