Giải bài tập SGK Toán 6 Bài 6: Tính chất của phép cộng các số nguyên

Tính:

a) \(126 + (-20) + 2004 + (-106)\);

b) \((-199) + (-200) + (-201)\).

Hướng dẫn giải

Câu a:

\(126 + (-20) + 2004 + (-106) \)

\(= 126+2004  + [(-20) + (-106)] \)

\(= 2004 + 126 + [- (20 + 106)] \) 

\(= 2004 + 126 + (-126)\) 

\(= 2004 + [126 + ( - 126)] \)

\(= 2004 + 0 = 2004.\)

Câu b:

\( (-199) + (-200) + (-201)\)

\(= (-199) + (-201) + (-200)\)

\(= [(-199) + (-201)] + (-200) \)

\(= - (199 + 201) + (-200)\)

\(=(-400)+(-200)\) 

\(= - (400 + 200) = -600.\)

Tìm tổng tất cả các số nguyên x, biết:

a) \( -4 < x < 3\);                       

b) \(-5 < x < 5\).

Hướng dẫn giải

Câu a:

Vì \( -4 < x < 3\) nên \(x\) nhận các giá trị: \(-3; -2; -1; 0; 1; 2\).

Khi đó ta có tổng sau: \((-3) + (-2) + (-1) + 0 + 1 + 2\) 

\(= (-3) +[ (-2) + 2 ]+ [(-1) + 1] + 0\) 

\(= (-3) + 0 + 0 + 0 = -3\). 

Câu b:

Vì \(-5 < x < 5\) nên \(x\) nhận các giá trị là: \(-4;-3;-2;-1;0;1;2;3;4\)

Khi đó ta có tổng sau:

\( (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4\)

\(=  [ (-4) + 4] + [ (-3) + 3] + [ (-2) + 2]\)\(\,+ [ (-1) + 1]  + 0\)

\(= 0+0+0+0+0=0\)

Tổng tất cả các số nguyên x thỏa mãn \(-5 < x < 5\) là \(0.\)

Chiếc diều của bạn Minh bay cao 15m (so với mặt đất). Sau một lúc, độ cao của chiếc diều tăng 2m, rồi sau đó lại giảm 3m. Hỏi chiếc diều ở độ cao bao nhiêu (so với mặt đất) sau hai lần thay đổi (h.47) ?

Hướng dẫn giải

Lần 1 diều của Minh tăng \(2m\) nên chiếc diều ở độ cao là:

\(15 + 2 = 17 (m) \)

Lần 2  diều của Minh  giảm \(3m \) nên chiếc diều ở độ cao là:

\(17 - 3 = 14 (m)\) 

Vậy chiếc diều của bạn Minh ở độ cao \(14m\) sau hai lần thay đổi. 

Tính:

a) \(1 + (-3) + 5 + (-7) + 9 + (-11)\);

b) \( (-2) + 4 + (-6) + 8 + (-10) + 12\).

Hướng dẫn giải

Câu a:

\(\eqalign{
& 1 + \left( { - 3} \right) + 5 + \left( { - 7} \right) + 9 + \left( { - 11} \right) \cr
& = \left( {1 + 9} \right) + \left[ {\left( { - 3} \right) + \left( { - 7} \right)} \right] + 5 + \left( { - 11} \right) \cr
& = 10 + \left[ { - \left( {3 + 7} \right)} \right] + 5 + \left( { - 11} \right) \cr
& = 10 + \left( { - 10} \right) + 5 + \left( { - 11} \right) \cr
& = 0 + 5 + \left( { - 11} \right) \cr
& = 5 + \left( { - 11} \right) = - \left( {11 - 5} \right) = - 6 \cr} \)

Câu b:

\((–2) + 4 + (–6) + 8 + (–10) + 12\) 

\(= [(–2) + 4] + [(–6) + 8] + [(–10) + 12]\)

\(= 2 + 2 + 2 = 6.\) 

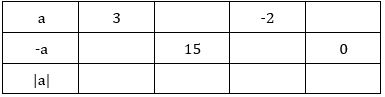
Điền số thích hợp vào ô trống:

Phương pháp giải

Hướng dẫn giải

Tính: 

a) (-38) + 28;              

b) 273 + (-123);             

c) 99 + (-100) + 101.

Hướng dẫn giải

Câu a:

\((-38) + 28 =  - ( 38 - 28) = -10\)

Câu b:

\(273 + (-123) = 273 - 123 = 150\)

Câu c:

\(99 + (-100) + 101\)

\( = (99 + 101) + (-100)\)

\( = 200 + (-100)\)

\( = 200 - 100\)

\(=100\). 

Tính nhanh 

a) \(217 + [43 + (-217) + (-23)]\);

b) Tổng của tất cả các số nguyên có giá trị tuyệt đối nhỏ hơn \(10\).

Hướng dẫn giải

Câu a:

\( 217 +[43 + (-217) + (-23)] \)

\(= 217 + 43 + (-217)+ (-23)\)

\(= 217 + (-217) + 43 + (-23) \)

\(= [217 + (-217)]+ [43 + (-23)]\) 

\(= 0 + (43 - 23) = 20\).

Câu b:

Các số nguyên có giá trị tuyệt đối nhỏ hơn \(10\) là:

\( -9; -8; -7; -6; -5; -4; -3; -2; -1;\)

\( 0; 1; 2; 3; 4; 5; 6; 7; 8; 9\)

Tổng các số trên là

\((-9) + (-8) + (-7) + (-6) +(-5) + (-4) \)

\(+ (-3) + (-2) + (-1) + 0 \)

\(+ 1 + 2 + 3 + 4 + 5 + 6 \)

\(+ 7 + 8 + 9\)

\(= [(-9) + 9] + [(-8) + 8] \)

\(+ [(-7) + 7] + [(-6) + 6]\)

\(+ [(-5) + 5] + [(-4) + 4] \)

\(+[(-3) +3] +[(-2) +2]\)

\(+ [(-1) +1] + 0 \)

\(=0+0+0+0+0\)

\(+0+0+0+0+0= 0\)

Hai ca nô cùng xuất phát từ C đi về phía A hoặc B (h.48).

Ta quy ước chiều từ C đến B là chiều dương (nghĩa là vận tốc và quãng đường đi từ C về phía B được biểu thị bằng số dương và theo chiều ngược lại là số âm).

Hỏi sau một giờ hai ca nô cách nhau bao nhiêu kilômét nếu vận tốc của chúng lần lượt là:

a) 10 km/h và 7km/h?

b) 10 km/h và -7km/h?

Hướng dẫn giải

Câu a:

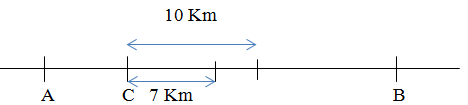
Vì vận tốc của hai ca nô đều dương nên hai ca nô cùng đi về phía B (chiều từ C đến B là chiều dương) nên khoảng cách sau 1 giờ của hai ca nô sẽ là hiệu quãng đường đi được của chúng.

- Sau 1 giờ, ca nô có vận tốc 10km/h đi được quãng đường là:

\(10.1=10 (km) \)

- Sau 1 giờ, ca nô có vận tốc 7km/h đi được quãng đường là:

\(7.1=7 (km)\) 

Vậy sau 1 giờ hai ca nô cách nhau:

\(10 - 7 = 3km\)

Câu b:

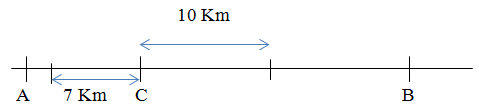
Ca nô có vận tốc 10km/h (là vận tốc dương) nên có chiều đi từ C đến B. Ca nô có vận tốc -7km/h (là vận tốc âm) nên có chiều đi từ C đến A.

Do đó hai ca nô đi ngược chiều nhau, nên khoảng cách sau 1 giờ của hai ca nô sẽ là tổng quãng đường đi được của chúng.

Vậy sau 1 giờ hai ca nô cách nhau: (quãng đường của mỗi ca nô đi được tính giống ở phần a)

10 + 7 = 17 (km)

Chú ý: Vận tốc -7km/h thì dấu "-" ở đây chỉ hướng đi của ca nô chứ không ảnh hưởng đến độ lớn của vận tốc hay quãng đường, nên khi tính quãng đường đi được vẫn ra số dương.  

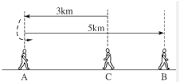
Hình 49 biểu diễn một người đi từ C đến A rồi quay về B. Hãy đặt một bài toán phù hợp với hình đó.

Hướng dẫn giải

Một người đi từ C đến A rồi quay trở về B như hình 49. 

Với quy ước rằng khi đi theo hướng từ C đến B thì quãng đường đi được biểu thị bởi số dương và theo hướng ngược lại thì được biểu thị bởi số âm.

Tính khoảng cách CB, biết rằng khoảng cách giữa A và C là 3km, khoảng cách giữa A và B là 5km.

Đố vui: Hai bạn Hùng và Vân tranh luận nhau: Hùng nói rằng có hai số nguyên mà tổng của chúng nhỏ hơn mỗi số hạng; Vân lại nói rằng không thể có được.

Theo bạn: Ai đúng? Nêu một ví dụ.

Hướng dẫn giải

Hùng nói đúng. Tổng của hai số âm đã cho là một số âm bé hơn cả hai số đã cho.

Ví dụ: \( (-4) + (-5) = (-9) \) 

Khi đó ta có: \( (-9) < (-4)\) ; \( (-9) < (-5)\)

Sử dụng máy tính bỏ túi

Nút [+/-]  dùng để đổi dấu "+" thành dấu "-" và ngược lại.

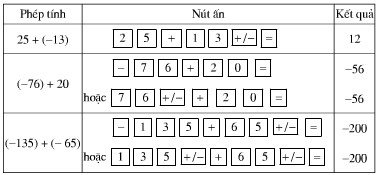
Dùng máy tính bỏ túi để tính:

a) 187 + (-54);       b) (-203) + 349;       c) (-175) + (-213).

Học sinh sử dụng máy tính cầm tay và thực hành các phép tính để có kết quả chính xác nhất.

Hướng dẫn giải

a) \(187 + (-54)=133\)

b) \((-203) + 349=146\)

c) \((-175) + (-213)=-388\)