Giải bài tập SGK Toán 6 Bài 5: Quy đồng mẫu số nhiều phân số

a) Quy đồng mẫu các phân số sau: \(\dfrac{-3}{16}; \dfrac{5}{24};\dfrac{-21}{56}\).

b) Trong các phân số đã cho, phân số nào chưa tối giản?

Từ nhận xét đó, ta có thể quy đồng các phân số này như thế nào? 

Phương pháp giải

a) Quy tắc quy đồng mẫu nhiều phân số:

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau: 

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

b) Phân số tối giản làm phân số mà ƯCLN của tử và mẫu bằng 1.

Hướng dẫn giải

Câu a:

Bước 1: Tìm một bội chung nhỏ nhất của các mẫu 16, 24, 56 để làm MSC

\(16 = 2^4\)

\(24 = 2^3.3\) 

\(56 = 2^3.7\)

\(\Rightarrow   BCNN(16, 24, 56) = 2^4.3.7 = 336\)

Do đó MSC của ba phân số là 336.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

- Thừa số phụ của 16 là 336 : 16 = 21

- Thừa số phụ của 24 là 336 : 24 = 14

- Thừa số phụ của 56 là 336 : 56 = 6

Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng:

\(\begin{array}{l}
\dfrac{{ - 3}}{{16}} = \dfrac{{ - 3.21}}{{16.21}} = \dfrac{{ - 63}}{{336}};\\
\dfrac{5}{{24}} = \dfrac{{5.14}}{{24.14}} = \dfrac{{70}}{{336}};\\
\dfrac{{-21}}{{56}} = \dfrac{{ - 21.6}}{{56.6}} = \dfrac{{ - 126}}{{336}};
\end{array}\)

Câu b:

Phân số \(\dfrac{-21}{56}\)  không phải là phân số tối giản.

Từ đó ta có: Để quy đồng mẫu các phân số đã cho, trước hết ta nên rút gọn các phân số đã cho thành phân số tối giản rồi hãy quy đồng mẫu. Nếu làm như vậy ta sẽ được các phân số đơn giản hơn:

Rút gọn: \(\displaystyle {{ - 21} \over {56}} = {{ - 21:7} \over {56:7}} = {-3 \over 8}\)

\(\Rightarrow  BCNN(16, 24, 8) = 2^4.3 = 48\)

- Thừa số phụ của 16 là 48 : 16 = 3

- Thừa số phụ của 24 là 48 : 24 = 2

- Thừa số phụ của 8 là 48 : 8 = 6

Ta có: 

\(\begin{array}{l}
\dfrac{{ - 3}}{{16}} = \dfrac{{ - 3.3}}{{16.3}} = \dfrac{{ - 9}}{{48}};\\
\dfrac{5}{{24}} = \dfrac{{5.2}}{{24.2}} = \dfrac{{10}}{{48}};\\
\dfrac{{-21}}{{56}} = \dfrac{{ - 3}}{8} = \dfrac{{ - 3.6}}{{8.6}} = \dfrac{{ - 18}}{{48}}
\end{array}\)

Quy đồng mẫu các phân số sau:

a) \(\dfrac{3}{8}\) và  \(\dfrac{5}{27}\);                

b) \(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\);                  

c) \(\dfrac{1}{15}\) và -6. 

Phương pháp giải

Quy tắc quy đồng mẫu nhiều phân số:

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Hướng dẫn giải

Câu a:

\(\dfrac{3}{8}\) và  \(\dfrac{5}{27}\) ;

Ta có:

\(8 = 2^3\)

\(27 = 3^3\) 

\(\Rightarrow  BCNN(8, 27) = 2^3.3^3 = 216\)

Nên mẫu số chung của hai phân số là 216.

- Thừa số phụ của 8 là 216 : 8 = 27

- Thừa số phụ của 27 là 216 : 27 = 8

Do đó:

\(\begin{array}{l}
\dfrac{{ 3}}{{8}} = \dfrac{{3.27}}{{8.27}} = \dfrac{{ 81}}{{216}};\\
\dfrac{5}{{27}} = \dfrac{{5.8}}{{27.8}} = \dfrac{{40}}{{216}};\\
\end{array}\)         

Câu b:

\(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)

\(BCNN(9,25) = 225\)

Thừa số phụ: \( 225: 9 = 25\)

\(225 : 25 = 9\) 

Khi đó ta nhân cả tử và mẫu của phân số thứ nhất với 25. Nhân cả tử và mẫu của phân số thứ hai với 9. Ta được

\(\begin{array}{l}
\dfrac{{ - 2}}{9} = \dfrac{{ - 2.25}}{{9.25}} = \dfrac{{ - 50}}{{225}};\\
\dfrac{4}{{25}} = \dfrac{{4.9}}{{25.9}} = \dfrac{{36}}{{225}} 
\end{array}\)  

Câu c:

\(\dfrac{1}{15}\) và \(-6=\dfrac{-6}{1}\)

\(BCNN(15,1) = 15\)

Khi đó ta giữ nguyên phân số đầu tiên. Phân số thứ 2 ta nhân cả tử và mẫu với 15.

\(\dfrac{1}{15}\) và \( - 6 = \dfrac{{ - 6}}{1} = \dfrac{{ - 6.15}}{{1.15}} = \dfrac{{ - 90}}{{15}}\) .

Quy đồng mẫu các phân số sau:

a) \(\dfrac{11}{120}\) và \(\dfrac{7}{40}\)

b) \(\dfrac{24}{146}\) và \(\dfrac{6}{13}\)

c) \(\dfrac{7}{30},\dfrac{13}{60},\dfrac{-9}{40}\)

d) \(\dfrac{17}{60},\dfrac{-5}{18},\dfrac{-64}{90}.\)

Phương pháp giải

- Quy tắc quy đồng mẫu nhiểu phân số:

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

- Ở câu d các em có thể rút gọn phân số \(\dfrac{-64}{90}\) rồi mới quy đồng, kết quả vẫn ra giống như trên. 

Hướng dẫn giải

Câu a:

\(\dfrac{11}{120}\) và \(\dfrac{7}{40}\)

\(\Rightarrow  BCNN(120,40) = 120\)

Thừa số phụ thứ nhất là: 120 : 120 = 1

Thừa số phụ thứ hai là: 120 : 40 = 3

Ta giữ nguyên phân số:  \(\dfrac{11}{120}\) 

\(\displaystyle {7 \over {40}} = {{7.3} \over {40.3}} = {{21} \over {120}}\);                                  

Câu b:

\(\dfrac{24}{146}\) và \(\dfrac{6}{13}\)

Rút gọn: \(\displaystyle {{24} \over {146}} = {{24:2} \over {146:2}} = {{12} \over {73}}\)

Ta đi quy đồng mẫu hai phân số sau: \(\dfrac{12}{73}\) và \(\dfrac{6}{13}\)

\(BCNN(73,13) =73.13= 949\) nên mẫu số chung là \(949\) 

Thừa số phụ thứ nhất là: 949 : 73 = 13

Thừa số phụ thứ hai là: 949 : 13 = 73

Ta có:

\(\displaystyle {{12} \over {73}} = {{12.13} \over {73.13}} = {{156} \over {949}}\)

\(\displaystyle {6 \over {13}} = {{6.73} \over {13.73}} = {{438} \over {949}}\)

Câu c:

\(\dfrac{7}{30},\dfrac{13}{60},\dfrac{-9}{40}\) ;                                

 Mẫu số chung là \(BCNN(30, 60, 40) = 120\)

Thừa số phụ thứ nhất là: \(120 : 30 =  4\)

Thừa số phụ thứ hai là: \(120 : 60 = 2\)

Thừa số phụ thứ ba là: \(120 : 40 =  3\)

Ta có:

\(\begin{array}{l}
\dfrac{7}{{30}} = \dfrac{{7.4}}{{30.4}} = \dfrac{{28}}{{120}};\\
\dfrac{{13}}{{60}} = \dfrac{{13.2}}{{60.2}} = \dfrac{{26}}{{120}};\\
\dfrac{{ - 9}}{{40}} = \dfrac{{ - 9.3}}{{40.3}} = \dfrac{{ - 27}}{{120}}.
\end{array}\)

Vậy ta được các phân số sau khi quy đồng là: \(\dfrac{28}{120},\dfrac{26}{120},\dfrac{-27}{120}\) ;

Câu d:

\(\dfrac{17}{60},\dfrac{-5}{18},\dfrac{-64}{90}.\)

Ta có: \(60=2^2.3.5;18=2.3^2;90=2.3^2.5\)

Mẫu số chung là \(BCNN(60,18,90) = 2^2.3^2.5=180\)

Thừa số phụ thứ nhất là: 180 : 60 =  3

Thừa số phụ thứ hai là: 180 : 18 = 10

Thừa số phụ thứ ba là: 180 : 90 = 2

Ta có: 

\(\begin{array}{l}
\dfrac{{17}}{{60}} = \dfrac{{17.3}}{{60.3}} = \dfrac{{51}}{{180}};\\
\dfrac{{ - 5}}{{18}} = \dfrac{{ - 5.10}}{{18.10}} = \dfrac{{ - 50}}{{180}};\\
\dfrac{{ - 64}}{{90}} = \dfrac{{ - 64.2}}{{90.2}} = \dfrac{{ - 128}}{{180}}.
\end{array}\)

Vậy ta được các phân số sau khi quy đồng là: \(\dfrac{51}{180},\dfrac{-50}{180},\dfrac{-128}{180}\).

Hai phân số sau đây có bằng nhau không?

a) \(\dfrac{-5}{14}\) và \(\dfrac{30}{-84}\);
b) \(\dfrac{-6}{102}\) và  \(\dfrac{-9}{153}\) .

Phương pháp giải

- Rút gọn để được những phân số tối giản rồi so sánh.

- Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.

Hướng dẫn giải

Câu a:

\(\dfrac{-5}{14}\) và \(\dfrac{30}{-84}\)

Ta có: \(\dfrac{{30}}{{ - 84}} = \dfrac{{30:(-6)}}{{ - 84:(-6)}} = \dfrac{-5}{{  14}};\)

Vậy: \(\dfrac{-5}{14}\) =  \(\dfrac{30}{-84}\)

Câu b:

\(\dfrac{-6}{102}\) và  \(\dfrac{-9}{153}\)

Ta  có:

\(\begin{array}{l}
\dfrac{{ - 6}}{{102}} = \dfrac{{ - 6:6}}{{102:6}} = \dfrac{{ - 1}}{{17}};\\
\dfrac{{ - 9}}{{153}} = \dfrac{{ - 9:9}}{{153:9}} = \dfrac{{ - 1}}{{17}}
\end{array}\)

Vậy: \(\dfrac{-6}{102}\) =  \(\dfrac{-9}{153}\)

Quy đồng mẫu số các phân số sau:

a) \(\displaystyle {{ - 4} \over 7},{8 \over 9},{{ - 10} \over {21}}\)                    

b) \(\displaystyle {5 \over {{2^2}.3}},{7 \over {{2^3}.11}}\)

Phương pháp giải

Quy tắc quy đồng mẫu nhiều phân số:

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Hướng dẫn giải

Câu a:

\(\eqalign{
& 9 = {3^2} \cr
& 21 = 3.7 \cr} \)

\(BCNN(7, 9, 21) = 63\) là mẫu số chung

Thừa số phụ thứ nhất là: 63: 7 =9

Thừa số phụ thứ hai là: 63: 9 = 7

Thừa số phụ thứ ba là: 63: 21 = 3

Quy đồng mẫu ta được: 

\(\eqalign{
& {{ - 4} \over 7} = {{\left( { - 4} \right).9} \over {7.9}} = {{ - 36} \over {63}} \cr
& {8 \over 9} = {{8.7} \over {9.7}} = {{56} \over {63}} \cr
& {{ - 10} \over {21}} = {{( - 10).3} \over {21.3}} = {{ - 30} \over {63}} \cr} \)

Câu b:

Mẫu số chung: \({2^3}.3.11 = 264\)

Thừa số phụ thứ nhất là: \(264:(2^2.3)=22\)

Thừa số phụ thứ hai là: \(264:(2^3.11)=3\)

Quy đồng mẫu ta được:

\(\eqalign{
& {5 \over {{2^2}.3}} = {{5.22} \over {{2^2}.3.22}} = {{110} \over {264}} \cr
& {7 \over {{2^3}.11}} = {{7.3} \over {{2^3}.11.3}} = {{21} \over {264}} \cr} \)

Quy đồng mẫu các phân số: 

a) \(\displaystyle {3 \over { - 20}},{{ - 11} \over { - 30}},{7 \over {15}}\)                    

b) \(\displaystyle {{ - 6} \over { - 35}},{{27} \over { - 180}}\), \(\displaystyle {{ - 3} \over { - 28}}\)

Đổi những phân số có mẫu âm thành những phân số có mẫu dương, rút gọn, rồi quy đồng. 

Phương pháp giải

- Đưa các phân số về mẫu dương rồi quy đồng.

- Quy tắc quy đồng mẫu nhiểu phân số: 

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Hướng dẫn giải

Câu a:

\(\displaystyle {3 \over { - 20}},{{ - 11} \over { - 30}},{7 \over {15}}\) 

\(\begin{array}{l}
\dfrac{3}{{ - 20}} = \dfrac{{3:\left( { - 1} \right)}}{{ - 20:\left( { - 1} \right)}} = \dfrac{{ - 3}}{{20}};\\
\dfrac{{ - 11}}{{ - 30}} = \dfrac{{ - 11:\left( { - 1} \right)}}{{ - 30:\left( { - 1} \right)}} = \dfrac{{11}}{{30}}
\end{array}\)

Khi đó ta cần quy đồng mẫu các phân số sau: \(\displaystyle {-3 \over {20}},{{  11} \over {  30}},{7 \over {15}}\)

\(20 = {2^2}.5\)

\(30 = 2.3.5\)

\(15=3.5\)

Mẫu số chung là \(BCNN(15, 20, 30)={2^2}.3.5=60\)

Thừa số phụ thứ nhất là: 60: 20= 3 

Thừa số phụ thứ hai là 60 : 30 = 2

Thừa số phụ thứ ba là: 60 : 15 = 4

Quy đồng mẫu ta được:

\(\eqalign{
& {3 \over { - 20}} = {{ - 3} \over {20}} = {{ - 3.3} \over {20.3}} = {{ - 9} \over {60}} \cr
& {{ - 11} \over { - 30}} = {{11} \over {30}} = {{11.2} \over {30.2}} = {{22} \over {60}} \cr
& {7 \over {15}} = {{7.4} \over {15.4}} = {{28} \over {60}} \cr} \)

Câu b:

\(\displaystyle {{ - 6} \over { - 35}},{{27} \over { - 180}}\), \(\displaystyle {{ - 3} \over { - 28}}\)

Rút gọn:\(\dfrac{{27}}{{ - 180}} = \dfrac{{27:\left( { - 9} \right)}}{{ - 180:\left( { - 9} \right)}} = \dfrac{{ - 3}}{{20}}\)

\(\dfrac{{ - 6}}{{ - 35}} = \dfrac{{ - 6:\left( { - 1} \right)}}{{ - 35:\left( { - 1} \right)}} = \dfrac{6}{{35}}\)

\(\dfrac{{ - 3}}{{ - 28}} = \dfrac{{ - 3:\left( { - 1} \right)}}{{ - 28:\left( { - 1} \right)}} = \dfrac{3}{{28}}\)

Khi đó ta quy đồng mẫu các phân số sau:  \(\displaystyle {{  6} \over { 35}},{{-3} \over { 20}}\), \(\displaystyle {{  3} \over {  28}}\)

\(35=5.7\)

\(20 = {2^2}.5\) 

\(28 = {2^2}.7\)

Mẫu số chung là \(BCNN(20,35,28)={2^2}.5.7 = 140\)

Thừa số phụ thứ nhất là: 140 : 35 = 4

Thừa số phụ thứ hai là: 140 : 20 = 7

Thừa số phụ thứ ba là: 140 : 28 = 5

Quy đồng mẫu ta được:  

\(\eqalign{
& {{ - 6} \over { - 35}} = {6 \over {35}} = {{6.4} \over {35.4}} = {{24} \over {140}} \cr
& {{27} \over { - 180}} = {{ - 3} \over {20}} = {{ - 3.7} \over {20.7}} = {{ - 21} \over {140}} \cr
& {{ - 3} \over { - 28}} = {3 \over {28}} = {{3.5} \over {28.5}} = {{15} \over {140}} \cr} \)

Quy đồng mẫu các phân số:

a) \( \displaystyle{{ - 5} \over 5},{8 \over 7}\)                

b) \( \displaystyle3,{{ - 3} \over 5},{{ - 5} \over 6}\)                    

c) \( \displaystyle{{ - 9} \over 7},{{ - 19} \over {15}}, - 1\) 

Phương pháp giải

Chú ý: \(\displaystyle 3 = {3 \over 1}, - 1 = {{ - 1} \over 1}\)

- Phân số nào chưa tối giản thì có thể rút gọn phân số trước khi quy đồng.

- Quy tắc quy đồng mẫu nhiểu phân số: 

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Hướng dẫn giải

Câu a:

\( \displaystyle{{ - 5} \over 5},{8 \over 7}\)

Rút gọn: \( \displaystyle{{ - 5} \over 5} =  - 1\)

Mẫu số chung là 7

Quy đồng ta được: 

\( \displaystyle - 1 = {{ - 7} \over 7}\) và \( \displaystyle{8 \over 7}\)

Câu b:

\( \displaystyle3,{{ - 3} \over 5},{{ - 5} \over 6}\)

Mẫu số chung là \(BCNN(5,6)=5.6=30\)

Thừa số phụ thứ nhất là: 30: 1 =  30

Thừa số phụ thứ hai là: 30 : 5 =  6

Thừa số phụ thứ ba là: 30 : 6 = 5

Quy đồng ta được:

\( \displaystyle\eqalign{
& 3 = {3 \over 1} = {{3.30} \over 30} = {{90} \over 30} \cr
& {{ - 3} \over 5} = {{\left( { - 3} \right).6} \over {5.6}} = {{ - 18} \over {30}} \cr
& {{ - 5} \over 6} = {{\left( { - 5} \right).5} \over {6.5}} = {{ - 25} \over {30}} \cr} \)

Câu c:

\( \displaystyle{{ - 9} \over 7},{{ - 19} \over {15}}, - 1\) 

Mẫu số chung là \(BCNN(15,7)=15.7=105\)

Thừa số phụ thứ nhất là: 105 : 7 = 15

Thừa số phụ thứ hai là: 105 : 15 = 7

Thừa số phụ thứ ba là: 105 : 1 = 105

Quy đồng ta được: 

\( \displaystyle\eqalign{
& {{ - 9} \over 7} = {{\left( { - 9} \right).15} \over {7.15}} = {{ - 135} \over {105}} \cr
& {{ - 19} \over {15}} = {{\left( { - 19} \right).7} \over {15.7}} = {{- 133} \over {105}} \cr
& - 1 = {{ - 1} \over 1} = {{\left( { - 1} \right).105} \over {1.105}} = {{ - 105} \over {105}} \cr} \)

Rút gọn rồi quy đồng mẫu các phân số:

a) \(\displaystyle {{ - 15} \over {90}},{{120} \over {600}},{{ - 75} \over {150}};\) 

b) \(\displaystyle {{54} \over { - 90}},{{ - 180} \over {288}},{{60} \over { - 135}}\) 

Phương pháp giải

- Rút gọn các phân số tối giản trước khi quy đồng.

Quy tắc rút gọn một phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.

- Quy tắc quy đồng mẫu nhiểu phân số: 

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu). 

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Hướng dẫn giải

Câu a:

\( \displaystyle{{ - 15} \over {90}},{{120} \over {600}},{{ - 75} \over {150}};\)

 Rút gọn:

\( \displaystyle\begin{array}{l}
\dfrac{{ - 15}}{{90}} = \dfrac{{ - 15:15}}{{90:15}} = \dfrac{{ - 1}}{6};\\
\dfrac{{120}}{{600}} = \dfrac{{120:120}}{{600:120}} = \dfrac{1}{5};\\
\dfrac{{ - 75}}{{150}} = \dfrac{{ - 75:75}}{{150:75}} = \dfrac{{ - 1}}{2}
\end{array}\)

Từ đó ta đi quy đồng 3 phân số sau: \( \displaystyle\dfrac{{ - 1}}{6};\dfrac{1}{5};\dfrac{{ - 1}}{2}\)

\(BCNN(6,5,2) = 30\)

Thừa số phụ thứ nhất là: 30: 6 = 5

Thừa số phụ thứ hai là: 30 : 5 = 6

Thừa số phụ thứ ba là: 30 : 2 = 15

Quy đồng mẫu ta được:

\( \displaystyle\eqalign{
& {{ - 1} \over 6} = {{\left( { - 1} \right).5} \over {6.5}} = {{ - 5} \over {30}} \cr
& {1 \over 5} = {{1.6} \over {5.6}} = {6 \over {30}} \cr
& {{ - 1} \over 2} = {{\left( { - 1} \right).15} \over {2.15}} = {{ - 15} \over {30}} \cr} \)

Câu b:

\( \displaystyle{{54} \over { - 90}},{{ - 180} \over {288}},{{60} \over { - 135}}\)

 Rút gọn

\( \displaystyle\begin{array}{l}
\dfrac{{54}}{{ - 90}} = \dfrac{{54:\left( { - 18} \right)}}{{ - 90:\left( { - 18} \right)}} = \dfrac{{ - 3}}{5};\\
\dfrac{{ - 180}}{{288}} = \dfrac{{ - 180:36}}{{288:36}} = \dfrac{{ - 5}}{8};\\
\dfrac{{ 60}}{{-135}} = \dfrac{{ 60:(-15)}}{{-135:(-15)}} = \dfrac{{ - 4}}{9}
\end{array}\)

Khi đó ta đi quy đồng mẫu các phân số mới sau: \( \displaystyle\dfrac{{ - 3}}{5};\dfrac{{ - 5}}{8};\dfrac{{ - 4}}{9}.\)

\(BCNN(5,8,9) = 360\)

Thừa số phụ thứ nhất là: 360: 5 = 72

Thừa số phụ thứ hai là: 360 : 8 = 45 

Thừa số phụ thứ ba là: 360 : 9 =  40

Quy đồng mẫu ta được:

\( \displaystyle\eqalign{
& {-3 \over 5} = {{(-3).72} \over {5.72}} = {{-216} \over {360}} \cr
& {{ - 5} \over 8} = {{\left( { - 5} \right).45} \over {8.45}} = {{ - 225} \over {360}} \cr
& {{ - 4} \over 9} = {{\left( { - 4} \right).40} \over {9.40}} = {{ - 160} \over {360}} \cr} \)

Đố vui: Hai bức ảnh dưới đây chụp di tích nào?

Cho các dãy phân số sau:

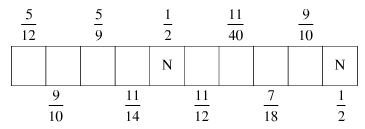
Hãy quy đồng mẫu các phân số của từng dãy rồi đoán nhận phân số thứ tư của dãy đó; viết nó dưới dạng tối giản rồi viết chữ cái ở dãy đó vào ô tương ứng với phân số ấy ở hình 6. Khi đó, em sẽ biết được hai địa danh của Việt Nam được UNESCO công nhận là di sản văn hóa thế giới vào năm 1999.

Chẳng hạn, ở dãy đầu có ghi chữ N, quy đồng mẫu ta được \( \displaystyle{2 \over {10}},{3 \over {10}},{4 \over {10}}\) nên phân số thứ tư là \( \displaystyle{5 \over {10}}\) . Nó có dạng tối giản \( \displaystyle{1 \over 2}\) , do đó ta điền chữ N vào hai ô ứng với số  \( \displaystyle{1 \over 2}\) trên hình 6. 

Phương pháp giải

Quy tắc quy đồng mẫu nhiểu phân số:

Muốn quy đồng mẫu nhiều phân số với mẫu dương ta làm như sau:

Bước 1: Tìm bội chung của các mẫu (thường là BCNN) để làm mẫu chung.

Bước 2: Tìm thừa số phụ của mỗi mẫu (bằng cách chia mẫu chung cho từng mẫu).

Bước 3: Nhân cả tử và mẫu của mỗi phân số với thừa số phụ tương ứng.

Hướng dẫn giải

Ta phải viết tiếp vào dãy số như sau:

\( \displaystyle N.\,\,\,\,\dfrac{2}{{10}};\dfrac{3}{{10}};\dfrac{4}{{10}};\dfrac{5}{{10}}\)

Điền chữ N vào ô \( \displaystyle \dfrac{5}{{10}} = \dfrac{1}{2}\)

\( \displaystyle M.\,\,\,{8 \over {12}};{9 \over {12}};{{10} \over {12}};{{11} \over {12}}\)

Điền chữ M vào ô \( \displaystyle \dfrac{11}{{12}} \)

\( \displaystyle H.\,\,{2 \over {12}};{3 \over {12}};{4 \over {12}};{5 \over {12}}\)

Điền chữ H vào ô \( \displaystyle \dfrac{5}{{12}} \)

\( \displaystyle S.\,\,{4 \over {18}};{5 \over {18}};{6 \over {18}};{7 \over {18}}\) 

Điền chữ S vào ô \( \displaystyle \dfrac{7}{{18}} \)

\( \displaystyle Y.\,\,{2 \over {40}};{5 \over {40}};{8 \over {40}};{{11} \over {40}}\) 

Điền chữ Y vào ô \( \displaystyle \dfrac{11}{{40}} \)

\( \displaystyle A.\,\,\,{2 \over {14}};{5 \over {14}};{8 \over {14}};{{11} \over {14}}\)

Điền chữ A vào ô \( \displaystyle \dfrac{11}{{14}} \)

\( \displaystyle O.\,\,{9 \over {20}};{{12} \over {20}};{{15} \over {20}};{{18} \over {20}} = {9 \over {10}}\)

Điền chữ O vào ô \( \displaystyle \dfrac{9}{{10}} \)

\( \displaystyle I.\,\,{1 \over {18}};{4 \over {18}};{7 \over {18}};{{10} \over {18}} = {5 \over 9}\)

Điền chữ I vào ô \( \displaystyle \dfrac{5}{{9}} \)

Vậy hai địa danh HỘI AN và MỸ SƠN của Viêt Nam được UNESCO công nhân là di sản văn hóa thế giới vào năm 1999.