Giải bài tập SGK Toán 6 Bài 4: Rút gọn phân số
Phần hướng dẫn giải bài tập SGK Rút gọn phân số sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập hai.
Mục lục nội dung
1. Giải bài 15 trang 15 SGK Toán 6 tập 2
2. Giải bài 16 trang 15 SGK Toán 6 tập 2
3. Giải bài 17 trang 15 SGK Toán 6 tập 2
4. Giải bài 18 trang 15 SGK Toán 6 tập 2
5. Giải bài 19 trang 15 SGK Toán 6 tập 2
6. Giải bài 20 trang 15 SGK Toán 6 tập 2
7. Giải bài 21 trang 15 SGK Toán 6 tập 2
8. Giải bài 22 trang 15 SGK Toán 6 tập 2
9. Giải bài 23 trang 16 SGK Toán 6 tập 2
10. Giải bài 24 trang 16 SGK Toán 6 tập 2
11. Giải bài 25 trang 16 SGK Toán 6 tập 2

1. Giải bài 15 trang 15 SGK Toán 6 tập 2
Rút gọn các phân số sau:
a) \(\dfrac{22}{55}\); b) \(\dfrac{-63}{81}\);
c) \(\dfrac{20}{-140}\); d) \(\dfrac{-25}{-75}\) .
Phương pháp giải
Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và - 1) của chúng.
Hướng dẫn giải
Câu a:
\(\dfrac{22}{55}=\dfrac{22:11}{55:11} = \dfrac{2}{5}\);
Câu b:
\(\dfrac{-63}{81}=\dfrac{-63:9}{81:9} = \dfrac{-7}{9}\);
Câu c:
\(\dfrac{20}{-140}= \dfrac{20:(-20)}{-140:(-20)} = \dfrac{-1}{7}\);
Câu d:
\(\dfrac{-25}{-75}= \dfrac{(-25):(-25)}{(-75):(-25)} = \dfrac{1}{3}\).
2. Giải bài 16 trang 15 SGK Toán 6 tập 2
Bộ răng đầy đủ của một người trưởng thành có 32 chiếc trong đó có 8 răng cửa, 4 răng nanh, 8 răng cối nhỏ và 12 răng hàm. Hỏi mỗi loại răng chiếm mấy phần của tổng số răng (Viết dưới dạng phân số tối giản).
Phương pháp giải
Ta lấy từng số răng chia cho tổng số răng rồi rút gọn về phân số tối giản.
Phân số tối giản (hay phân số không rút gọn được nữa) là phân số mà tử và mẫu chỉ có ước chung là 1 và - 1
Hướng dẫn giải
Răng cửa chiếm \( \displaystyle{8 \over {32}} = {{8:8} \over {32:8}} = \dfrac{1}{4}\) tổng số răng.
Răng nanh chiếm \( \displaystyle{4 \over {32}} = {{4:4} \over {32:4}} = \dfrac{1}{8}\) tổng số răng.
Răng cối nhỏ chiếm \( \displaystyle{8 \over {32}} = {{8:8} \over {32:8}} = \dfrac{1}{4}\) tổng số răng.
Răng hàm chiếm \( \displaystyle{{12} \over {32}} = {{12:4} \over {32:4}} = \dfrac{3}{8}\) tổng số răng.
3. Giải bài 17 trang 15 SGK Toán 6 tập 2
Rút gọn:
a) \(\dfrac{3.5}{8.24}\); b) \(\dfrac{2.14}{7.8}\)
c) \(\dfrac{3.7.11}{22.9}\); d) \(\dfrac{8.5-8.2}{16}\) ;
e) \(\dfrac{11.4-11}{2-13}\) .
Phương pháp giải
Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và - 1) của chúng.
Lưu ý: Ta có thể phân tích tử và mẫu của phân số ra thừa số nguyên tố rồi chia cả tử và mẫu cho thừa số chung.
Hướng dẫn giải
Câu a:
\(\dfrac{3.5}{8.24}=\dfrac{3.5:3}{8.24:3}=\dfrac{5}{8.8}=\dfrac{5}{64}\) .
Câu b:
\(\dfrac{2.14}{7.8}=\dfrac{2.2.7}{7.2.2.2}=\dfrac{1}{2};\)
Câu c:
\(\dfrac{3.7.11}{22.9}=\dfrac{3.7.11}{2.11.3.3}=\dfrac{7}{2.3}=\dfrac{7}{6};\)
Câu d:
\(\dfrac{{8.5 - 8.2}}{{16}} = \dfrac{{8.(5 - 2)}}{{2.8}} = \dfrac{{8.3}}{{2.8}} = \dfrac{3}{2}\)
Câu e
\(\dfrac{{11.4 - 11}}{{2 - 13}} = \dfrac{{11.4 - 11.1}}{{ - 11}}\)
\(\, = \dfrac{{11.(4 - 1)}}{{ - 11}} = \dfrac{{11.3}}{{ - 11}} = \dfrac{3}{{ - 1}} = - 3.\)
4. Giải bài 18 trang 15 SGK Toán 6 tập 2
Viết các số đo thời gian sau đây với đơn vị là giờ (chú ý rút gọn nếu có thể).
a) 20 phút
b) 35 phút
c) 90 phút.
Phương pháp giải
Muốn đổi từ phút ra giờ ta lấy số phút chia cho 60.
Hướng dẫn giải
Câu a:
20 phút \(= \dfrac{{20}}{{60}}\) giờ \( = \dfrac{{20:20}}{{60:20}}\) giờ \(=\dfrac{1}{3}\) giờ ;
Câu b:
35 phút \( = \dfrac{{35}}{{60}}\) giờ \( = \dfrac{{35:5}}{{60:5}}\) giờ \(=\dfrac{7}{12}\) giờ ;
Câu c:
90 phút \( = \dfrac{{90}}{{60}}\) giờ \( = \dfrac{{90:30}}{{60:30}}\) giờ \(=\dfrac{3}{2}\) giờ.
5. Giải bài 19 trang 15 SGK Toán 6 tập 2
Đổi ra mét vuông (viết dưới dạng phân số tối giản):
25 dm2; 36 dm2;
450 cm2; 575 cm2.
Phương pháp giải
1m2 = 100 dm2 = 10000 cm2
Suy ra: \(1dm^2=\dfrac{1}{100}m^2;1cm^2=\dfrac{1}{10000}m^2\)
Hướng dẫn giải
Ta có: \(1dm^2=\dfrac{1}{100}m^2;1cm^2=\dfrac{1}{10000}m^2\) nên:
25 dm2 \(=\dfrac{25}{100}m^2\)\(=\dfrac{25}{4.25}m^2\) \(=\dfrac{1}{4}\) m2 ;
36 dm2 \(=\dfrac{36}{100}m^2\) \(=\dfrac{9.4}{25.4}m^2\)\(=\dfrac{9}{25}\) m2 ;
450 cm2 \(=\dfrac{450}{10000}m^2\) \(=\dfrac{9.50}{200.50}m^2\)\(=\dfrac{9}{200}\) m2;
575 cm2 \(=\dfrac{575}{10000}m^2\)\(=\dfrac{23.25}{400.25}m^2\)\(=\dfrac{23}{400}\) m2
6. Giải bài 20 trang 15 SGK Toán 6 tập 2
Tìm các cặp phân số bằng nhau trong các phân số sau đây:
\(\displaystyle {{ - 9} \over {33}};{{15} \over 9};{3 \over { - 11}};{{ - 12} \over {19}};{5 \over 3};{{60} \over { - 95}}\)
Phương pháp giải
Rút gọn các phân số chưa tối giản để xuất hiện các phân số bằng nhau.
Hướng dẫn giải
\(\displaystyle {{ - 9} \over {33}} = {{ - 9:\left( { - 3} \right)} \over {33:\left( { - 3} \right)}} = {3 \over { - 11}}; \)\(\displaystyle {{15} \over 9} = {{15:3} \over {9:3}} = {5 \over 3};\)
\(\displaystyle {{ - 60} \over {95}} = {{ - 60:\left( { - 5} \right)} \over {95:\left( { - 5} \right)}} = {{-12} \over { 19}}\)
Vậy ta có các cặp phân số bằng nhau là:
\(\dfrac{{ - 9}}{{33}} = \dfrac{3}{{ - 11}};\,\,\,\dfrac{{15}}{9} = \dfrac{5}{3};\)
\(\dfrac{{60}}{{ - 95}} = \dfrac{{ - 12}}{{19}}\)
7. Giải bài 21 trang 15 SGK Toán 6 tập 2
Trong các phân số sau đây, tìm phân số không bằng phân số nào trong các phân số còn lại:
\(\displaystyle {{ - 7} \over {42}};{{12} \over {18}};{3 \over { - 18}};{{ - 9} \over {54}};{{ - 10} \over { - 15}};{{14} \over {20}}\)
Phương pháp giải
Gợi ý: Rút gọn các phân số về phân số tối giản, sau đó so sánh để tìm ra phân số không bằng các phân số còn lại.
Hướng dẫn giải
\(\dfrac{{ - 7}}{{42}} = \dfrac{{ - 7:7}}{{42:7}} = \dfrac{{ - 1}}{6};\\\dfrac{3}{{ - 18}} = \dfrac{{3:\left( { - 3} \right)}}{{ - 18:\left( { - 3} \right)}} = \dfrac{{ - 1}}{6};\\
\dfrac{{ - 9}}{{54}} = \dfrac{{ - 9:9}}{{54:9}} = \dfrac{{ - 1}}{6};\)
Suy ra \( \dfrac{{ - 7}}{{42}} = \dfrac{3}{{ - 18}} = \dfrac{{ - 9}}{{54}}\)
\(\dfrac{{12}}{{18}} = \dfrac{{12:6}}{{18:6}} = \dfrac{2}{3};\\\dfrac{{ - 10}}{{ - 15}} = \dfrac{{ - 10:\left( { - 5} \right)}}{{ - 15:\left( { - 5} \right)}} = \dfrac{2}{3};\)
Suy ra \(\dfrac{{12}}{{18}} = \dfrac{{ - 10}}{{ - 15}}\)
\(\dfrac{{14}}{{20}} = \dfrac{{14:2}}{{20:2}} = \dfrac{7}{{10}}\)
Như vậy ta có trong các phân số trên thì phân số không bằng phân số nào trong các phân số còn lại là: \(\dfrac{{14} }{ {20}}\)
8. Giải bài 22 trang 15 SGK Toán 6 tập 2
Điền số thích hợp vào chỗ trống:
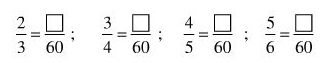
Phương pháp giải
Lấy 60 chia cho từng mẫu số rồi nhân tử số tương ứng với thương thu được.
Hướng dẫn giải
Cách 1:
\(\dfrac{2}{3} = \dfrac{{40}}{{60}};\dfrac{3}{4} = \dfrac{{45}}{{60}};\dfrac{4}{5} = \dfrac{{48}}{{60}};\dfrac{5}{6} = \dfrac{{50}}{{60}}\)
Giải thích rõ hơn để ra được đáp án đó:
\(\begin{array}{l}
\dfrac{2}{3} = \dfrac{{2.20}}{{3.20}} = \dfrac{{40}}{{60}};\\
\dfrac{3}{4} = \dfrac{{3.15}}{{4.15}} = \dfrac{{45}}{{60}};\\
\dfrac{4}{5} = \dfrac{{4.12}}{{5.12}} = \dfrac{{48}}{{60}};\\
\dfrac{5}{6} = \dfrac{{5.10}}{{6.10}} = \dfrac{{50}}{{60}};
\end{array}\)
Cách 2:
Coi số cần điền vào ô vuông là \(x\), ta có:
\(\dfrac{2}{3} = \dfrac{x}{{60}}\)
Suy ra:
\(\begin{array}{l}
3.x = 2.60\\
3x = 120\\
x = 120:3\\
x = 40
\end{array}\)
Vậy \(\dfrac{2}{3} = \dfrac{40}{{60}}\)
\(\dfrac{3}{4} = \dfrac{x}{{60}}\)
Suy ra:
\(\begin{array}{l}
4.x = 3.60\\
4x = 180\\
x = 180:4\\
x = 45
\end{array}\)
Vậy \(\dfrac{3}{4} = \dfrac{45}{{60}}\)
\(\dfrac{4}{5} = \dfrac{x}{{60}}\)
Suy ra:
\(\begin{array}{l}
5.x = 4.60\\
5x = 240\\
x = 240:5\\
x = 48
\end{array}\)
Vậy \(\dfrac{4}{5} = \dfrac{48}{{60}}\)
\(\dfrac{5}{6} = \dfrac{x}{{60}}\)
Suy ra:
\(\begin{array}{l}
6.x = 5.60\\
6x = 300\\
x = 300:6\\
x = 50
\end{array}\)
Vậy \(\dfrac{5}{6} = \dfrac{50}{{60}}\)
9. Giải bài 23 trang 16 SGK Toán 6 tập 2
Cho tập hợp \(A = \{0;-3;5\}.\) Viết tập hợp B các phân số \(\dfrac{m}{n}\) mà \(m, n ∈ A.\)
(Nếu có hai phân số bằng nhau thì chỉ cần viết một phân số).
Phương pháp giải
Ta lấy số đầu làm tử và mẫu là chính số đó hoặc hai số còn lại, tiếp đến lấy số thứ hai làm tử, hai số kia làm mẫu ... (loại các phân số có mẫu bằng 0).
Hướng dẫn giải
Vì 0 không thể là mẫu số nên các phân số phải tìm chỉ có thể có mẫu bằng \(- 3\) hoặc \(5.\)
Các phân số có mẫu bằng -3 là \(\displaystyle {0 \over { - 3}},{{ - 3} \over { - 3}},{5 \over { - 3}}\)
Các phân số có mẫu bằng 5 là: \(\displaystyle {0 \over 5},{{ - 3} \over 5},{5 \over 5}\)
Nhưng ta thấy \(\displaystyle {0 \over { - 3}} = 0 = {0 \over 5},{{ - 3} \over { - 3}} = 1 = {5 \over 5}\)
Vậy chỉ có bốn phân số khác nhau: \(\dfrac{0}{5}, \dfrac{5}{5},\) \(\displaystyle {5 \over { - 3}},{{ - 3} \over 5}\)
Từ đó tập hợp \(B = \left\{ {\dfrac{0}{5};\dfrac{5}{5};\dfrac{{ - 3}}{5};\dfrac{5}{{ - 3}}} \right\}\)
10. Giải bài 24 trang 16 SGK Toán 6 tập 2
Tìm các số nguyên x và y, biết:
\(\displaystyle {3 \over x} = {y \over {35}} = {{ - 36} \over {84}}\)
Phương pháp giải
Ta có \(\dfrac{a}{b}=\dfrac{c}{d}\) khi \(a.d=b.c\)
Hướng dẫn giải
Ta có: \(\dfrac{3}{x} = \dfrac{y}{{35}} = \dfrac{{ - 36}}{{84}}\)
mà \(\dfrac{{ - 36}}{{84}} = \dfrac{{ - 36:12}}{{84:12}} = \dfrac{-3}{7}\)
Do đó
+) \(\dfrac{3}{x} = \dfrac{{ - 3}}{7}\), suy ra \(x.\left( { - 3} \right) = 3.7\) hay \(x = 21:\left( { - 3} \right) = - 7\)
+) \(\dfrac{y}{{35}} = \dfrac{{ - 3}}{7}\), suy ra \(7y = 35.\left( { - 3} \right)\) hay \(y = - 105:7 = - 15\)
Đáp số: \(x = - 7;y = - 15\)
11. Giải bài 25 trang 16 SGK Toán 6 tập 2
Viết tất cả các phân số bằng \(\displaystyle {{15} \over {39}}\) mà tử và mẫu là các số tự nhiên có hai chữ số.
Phương pháp giải
Bước 1: Ta tối giản phân số đã cho
Bước 2: Sau đó nhân tử và mẫu của phân số tối giản đó lần lượt với các số tự nhiên 2, 3, 4, 5, ... cho đến khi tử số và mẫu số vẫn là hai chữ số.
Hướng dẫn giải
Bước 1:
Rút gọn: \(\dfrac{{15}}{{39}} \)\(= \dfrac{{15:3}}{{39:3}} \)\(= \dfrac{5}{{13}}\)
Bước 2:
Ta có:
\(\eqalign{
& {5 \over {13}} = {{5.2} \over {13.2}} = {{10} \over {26}} \cr
& {5 \over {13}} = {{5.3} \over {13.3}} = {{15} \over {39}} \cr
& {5 \over {13}} = {{5.4} \over {13.4}} = {{20} \over {52}} \cr
& {5 \over {13}} = {{5.5} \over {13.5}} = {{25} \over {65}} \cr
& {5 \over {13}} = {{5.6} \over {13.6}} = {{30} \over {78}} \cr
& {5 \over {13}} = {{5.7} \over {13.7}} = {{35} \over {91}} \cr} \)
Vậy các phân số bằng \(\displaystyle {{15} \over {39}}\) mà tử và mẫu là các số tự nhiên có hai chữ số là:
\(\displaystyle {{10} \over {26}};{{15} \over {39}};{{20} \over {52}},{{25} \over {65}};{{30} \over {78}};{{35} \over {91}}\)
12. Giải bài 26 trang 16 SGK Toán 6 tập 2
Cho đoạn thẳng AB:

Hãy vẽ vào vở các đoạn thẳng CD, EF, GH, IK biết rằng:
\(\displaystyle CD = {3 \over 4}AB;EF = {5 \over 6}AB;GH = {1 \over 2}AB;\)\(\displaystyle IK = {5 \over 4}AB.\)
Phương pháp giải
Đếm số phần của đoạn thẳng AB, sau đó đưa các phân số về các phân số có mẫu bằng với số phần của đoạn AB.
Từ đó vẽ hình.
Hướng dẫn giải
Đoạn AB được chia thành 12 đoạn nhỏ bằng nhau.
Do đó \(\displaystyle CD = {3 \over 4}AB = {9 \over {12}}AB.\)
\(\begin{array}{l}
EF = \dfrac{5}{6}AB = \dfrac{{10}}{{12}}AB;\\
GH = \dfrac{1}{2}AB = \dfrac{6}{{12}}AB;\\
IK = \dfrac{5}{4}AB = \dfrac{{15}}{{12}}AB;
\end{array}\)
Vậy nếu AB bằng 12 đoạn nhỏ thì CD bằng 9 đoạn nhỏ, EF bằng 10 đoạn nhỏ, GH bằng 6 đoạn nhỏ, IK bằng 15 đoạn nhỏ.
Ta có hình vẽ:
\(CD=\dfrac{3}{4}AB\)
\(EF=\dfrac{5}{6}AB\)
\(GH=\dfrac{1}{2}AB\)
\(IK=\dfrac{5}{4}AB\)
13. Giải bài 27 trang 16 SGK Toán 6 tập 2
Đố: Một học sinh đã “ rút gọn” như sau:
\(\displaystyle {{10 + 5} \over {10 + 10}} = {5 \over {10}} = {1 \over 2}\)
Bạn đó giải thích: “Trước hết em rút gọn cho 10, rồi rút gọn cho 5”. Đố em làm như vậy đúng hay sai? Vì sao?
Phương pháp giải
Quy tắc rút gọn phân số: Muốn rút gọn một phân số, ta chia cả tử và mẫu của phân số cho một ước chung (khác 1 và -1) của chúng.
Hướng dẫn giải
Bạn học sinh này đã làm sai.
Vì theo quy tắc rút gọn, ta phải chia cả tử và mẫu của phân số cho cùng một số khác 0, nhưng học sinh này đã trừ cả tử và mẫu cho 10.
Có thể trình bày lại như sau:
\(\dfrac{{10 + 5}}{{10 + 10}} = \dfrac{{15}}{{20}} = \dfrac{{15:5}}{{20:5}} = \dfrac{3}{4}\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Mở rộng khái niệm về phân số
- doc Giải bài tập SGK Toán 6 Bài 2: Phân số bằng nhau
- doc Giải bài tập SGK Toán 6 Bài 3: Tính chất cơ bản của phân số
- doc Giải bài tập SGK Toán 6 Bài 5: Quy đồng mẫu số nhiều phân số
- doc Giải bài tập SGK Toán 6 Bài 6: So sánh phân số
- doc Giải bài tập SGK Toán 6 Bài 7: Phép cộng phân số
- doc Giải bài tập SGK Toán 6 Bài 8: Tính chất cơ bản của phép cộng phân số
- doc Giải bài tập SGK Toán 6 Bài 9: Phép trừ phân số
- doc Giải bài tập SGK Toán 6 Bài 10: Phép nhân phân số
- doc Giải bài tập SGK Toán 6 Bài 11: Tính chất cơ bản của phép nhân phân số
- doc Giải bài tập SGK Toán 6 Bài 12: Phép chia phân số
- doc Giải bài tập SGK Toán 6 Bài 13: Hỗn số. Số thập phân. Phần trăm
- doc Giải bài tập SGK Toán 6 Bài 14: Tìm giá trị phân số của một số cho trước
- doc Giải bài tập SGK Toán 6 Bài 15: Tìm một số biết giá trị một phân số của nó
- doc Giải bài tập SGK Toán 6 Bài 16: Tìm tỉ số của hai số
- doc Giải bài tập SGK Toán 6 Bài 17: Biểu đồ phần trăm
- doc Giải bài tập SGK Toán 6 Ôn tập Chương 3: Phân số
- doc Giải bài tập SGK Toán 6 Ôn tập cuối năm

.JPG)
.JPG)
.JPG)
