Giải bài tập SGK Toán 6 Bài 9: Quy tắc chuyển vế

Tìm số nguyên x, biết:

a) \(7 - x = 8 - (-7)\);                      

b) \( x - 8 = (-3) - 8\).

Hướng dẫn giải

Câu a

\(7 - x = 8 - (-7) \)

\(7 - x = 8+7\) 

\(7 - x = 15\) 

\(  - x = 15 - 7\)

\( - x = 8\)

\( x = -8\) 

Cách khác: 

\(7 - x = 8 - (-7) \)

\(7 - x = 8 +7 \)

\(- x = 8+7-7\)

\(-x = 8\)

\( x = - 8\) 

Câu b

\(x - 8 = (-3) - 8\).

\(x - 8 = -(3+8)\)

\(x - 8 = (-11)\)

\( x =(-11) + 8\)

\(x = - 3\)

Cách khác: 

\(x - 8 = (-3) - 8\).

\(x =  (-3) - 8+8\)

\(x =  (-3) +8-8\)

\( x =-3 + 0\)

\(x = - 3\) 

Tìm số nguyên a, biết:

a) \(\left | a \right |\) = 2;           b) \(\left | a + 2\right |\) = 0.

Hướng dẫn giải

Câu a:

\(\left | a \right | = 2\)

Suy ra \(a=  2\) hoặc \(a = -2\)

Câu b:

Có duy nhất một số có giá trị tuyệt đối bằng 0 là 0. 

\(\left | a + 2\right |\) = 0

Suy ra \(a + 2 = 0\).

Do đó \(a = 0-2=-2\) (chuyển vế đổi dấu) 

Tìm số nguyên x, biết rằng tổng của ba số: 3, -2 và x bằng 5.

Hướng dẫn giải

Tổng của ba số: 3, - 2 và x bằng 5 nên ta có:

\(3 + (-2) + x = 5\)

\(3-2 + x = 5\)

 \(  1  + x = 5\)

\( x = 5 - 1\)

\( x = 4\)

Vậy \( x = 4\).

Cho a ∈ Z. Tìm số nguyên x, biết:

a) \(a + x = 5\);            b)  \(a - x = 2\).

Hướng dẫn giải

Câu a:

\(a + x = 5\). 

Chuyển \(a\) từ vế trái sang vế phải ta được: \(x = 5 - a\)

Vậy \(x = 5 - a.\)

Câu b:

\(a - x = 2\). 

Chuyển \(-x \) từ vế trái sang vế phải và chuyển \(2\) từ vế phải sang vế trái ta được:

\(a - 2 = x\).

Vậy \(x = a - 2\).

Cho \(a, b ∈\mathbb Z.\) Tìm số nguyên \(x\), biết: 

a) \( a + x = b\); 

b) \(a - x = b\).

Hướng dẫn giải

Câu a:

\( a + x = b\)

\(  x = b - a\)  (chuyển a từ vế trái sang vế phải)                

Câu b:

\(a - x = b\)

\(a - b = x\) (chuyển - x từ vế trái sang vế phải, chuyển b từ vế phải sang vế trái)

\(x = a - b\) 

Tìm số nguyên x, biết: \(4 - (27 - 3) = x - (13 - 4)\) 

Hướng dẫn giải

\(4 - (27 - 3) = x - (13 - 4)\)

\(4 - 24         = x - 9\)

\((-20)          = x - 9\)

\((-20) + 9    = x\)

\(   -11         = x \)

\(x = -11\)

Vậy \(x = -11\) 

Cách khác:

\(4 – (27 – 3) = x – (13 – 4)\)

\(4 – 27 + 3 = x – 13 + 4\) (bỏ ngoặc)

\(4 – 27 + 3 + 13 – 4 = x\) (chuyển vế –13 và 4)

\(4-4–27 + 3+13 = x\)

\(-27+16=x\) 

\(–11 = x\)

\(x = -11\)

Tính: 

a) \( (-37) + (-112)\);

b) \( (-42) + 52\); 

c) \( 13 - 31\);

d) \( 14 - 24 - 12\);  

e) \( (-25) + 30 - 15\). 

Hướng dẫn giải

Câu a:

\( (-37) + (-112)\) \(= - (37 + 112) = - 149\)

Câu b:

\( (-42) + 52\) \( =52 - 42 = 10 \)

Câu c:

\( 13 - 31\)  \( = - (31 - 13) = -18\)

Câu d:

\( 14 - 24 - 12\) 

\( = 14 - (24 + 12) \)

\(= 14 - 36 = -(36 - 14) = -22\)

Câu e:

\( (-25) + 30 - 15\)

\( = 30 - (25 + 15 ) \)

\(= 30 - 40 = - (40 - 30) = -10\)

Một đội bóng đá năm ngoái ghi được 27 bàn và để thủng lưới 48 bàn. Năm nay đội ghi được 39 bàn và để thủng lưới 24 bàn. Tính hiệu số bàn thắng - thua của đội đó trong mỗi mua giải.

Hướng dẫn giải

Năm ngoái:

Bàn thắng: 27 bàn 

Bàn thua: 48 bàn

Hiệu số bàn thắng - thua năm ngoái là: \( 27 - 48 =- (48 -27)  =  -21\) (bàn) 

Năm nay:

Bàn thắng: 39 bàn

Bàn thua: 24 bàn.

Hiệu số bàn thắng - thua năm nay là: \( 39 - 24 = 15 \) (bàn)

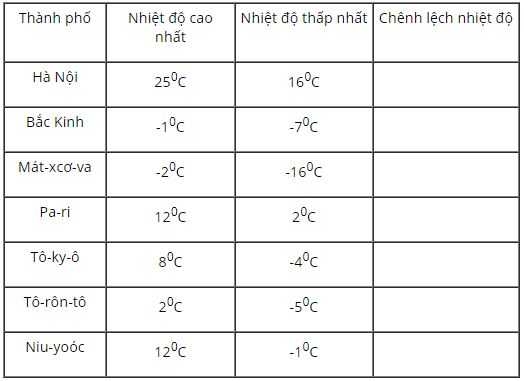
Trong bảng dưới đây có nhiệt độ cao nhất và nhiệt độ thấp nhất của mỗi số thành phố vào mỗi ngày nào đó. Hãy ghi vào cột bên phải số độ chênh lệch (nhiệt độ cao nhất trừ nhiệt độ thấp nhất) trong ngày đó của mỗi thành phố.

Hướng dẫn giải

Cụ thể:

Thành phố Hà Nội: \(25 – 16 = 9 \)

Thành phố Bắc Kinh: \((–1) – (–7) = –1 + 7 = 6.\)

Thành phố Mát– xcơ–va: \((–2) – (–16) \)\(= –2 + 16 = 14.\)

Thành phố Pa–ri: \(12 – 2 = 10\)

Thành phố Tô–ky–ô: \(8 – (–4) = 8 + 4 = 12.\)

Thành phố Tô–rôn–tô: \(2 – (–5) = 2 + 5 = 7\)

Thành phố Niu–yooc: \(12 – (–1) = 12 + 1 = 13.\)

Tính các tổng sau một cách hợp lí:

a) \(3784 + 23 - 3785 - 15\);

b) \(21 + 22 + 23 + 24 - 11 - 12 - 13 - 14\).

Hướng dẫn giải

Câu a:

\(3784 + 23 - 3785 - 15\) 

\(= (3784 - 3785) + (23 - 15)\)

\(= - (3785 - 3784) + 8 \)

\(=         -1            +    8\)

\(=                    7\)

Câu b:

\(21 + 22 + 23 + 24 - 11 - 12 - 13 - 14\)

\(= (21 - 11) + (22 - 12) + (23 - 13) + (24 - 14)\)

\(=      10      +     10       +      10      +    10\)

\(=                                 40\) 

Tính nhanh:

a)\( -2001 + (1999 + 2001)\);

b)\(  (43 - 863) - (137 - 57)\).

Hướng dẫn giải

Câu a

\( -2001 + (1999 + 2001) = -2001 + 1999 + 2001 \)

\( = (- 2001 + 2001) +1999 = 0 + 1999 = 1999 \) 

Câu b

\(  (43 - 863) - (137 - 57) =  43 - 863 - 137 + 57\)

\( = (43 + 57 ) - (  863 + 137 ) =100  - 1000 \)

\(= - ( 1000 - 100 )\) \( = - 900\)

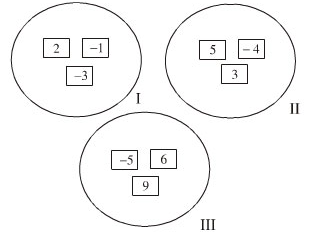
Đố: Cho chín tấm bìa có ghi số và chia thành ba nhóm như hình 51. Hãy chuyển một tấm, bìa từ nhóm này sang nhóm khác sao cho tổng các số trong mỗi nhóm đều bằng nhau. 

Hướng dẫn giải

Tổng tất cả các số trong cả 3 nhóm là:

\(2 + (-1) + (-3) + 5 + 3 + (-4) + (-5) + 6 + 9 \)

\(=  (-3) + 3 + (-5) + 5 +(-4) + (-1)  + (2 + 6 + 9)\)

\( =0+0+(-5)+ 17= 12\) 

Do tổng các số trong mỗi nhóm bằng nhau nên mỗi nhóm phải có tổng là:

\(12 : 3 = 4\) 

Ta thấy:

Nhóm II có \( 5 + 3 + (-4) = 4 \) nên giữ nguyên

Nhóm III có \( 6 + 9 + (-5) = 10 \) nên bớt 6 để có tổng bằng 4 (vì \(10 – 6 = 4)\)

Nhóm I có \(2 + (-3) + (-1) = -2 \) nên thêm 6 để có tổng bằng 4 (vì \(-2 + 6 = 4)\) 

Vậy ta chỉ cần chuyền bìa số 6 từ nhóm III sang nhóm I thì tổng mỗi nhóm đều bằng 4.