Giải bài tập SGK Toán 6 Bài 11: Nhân hai số nguyên cùng dấu
Phần hướng dẫn giải bài tập SGK Nhân hai số nguyên cùng dấu sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập một.
Mục lục nội dung
1. Giải bài 78 trang 91 SGK Toán 6 tập 1
2. Giải bài 79 trang 91 SGK Toán 6 tập 1
3. Giải bài 80 trang 91 SGK Toán 6 tập 1
4. Giải bài 81 trang 91 SGK Toán 6 tập 1
5. Giải bài 82 trang 92 SGK Toán 6 tập 1
6. Giải bài 83 trang 92 SGK Toán 6 tập 1
7. Giải bài 84 trang 92 SGK Toán 6 tập 1
8. Giải bài 85 trang 92 SGK Toán 6 tập 1
9. Giải bài 86 trang 92 SGK Toán 6 tập 1
10. Giải bài 87 trang 92 SGK Toán 6 tập 1

1. Giải bài 78 trang 91 SGK Toán 6 tập 1
Tính:
a) \((+3) . (+9)\) b) \((-3) . 7\)
c) \(13 . (-5)\) d) \((-150) . (-4)\)
e) \((+7) . (-5)\).
Phương pháp giải
a) Nhân hai số nguyên dương: ta nhân như hai số tự nhiên.
b, c, e) Muốn nhân hai số nguyên khác dấu ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu \("-"\) trước kết quả.
d) Muốn nhân hai số nguyên âm, ta nhân hai giá trị tuyệt đối của chúng.
Hướng dẫn giải
Câu a:
\((+3) . (+9) = 3.9 = 27\)
Câu b:
\((-3) . 7 = -(3.7) = -21\)
Câu c:
\(13 . (-5) = - (13.5) = -65 \)
Câu d:
\((-150) . (-4) = 150 . 4 =600 \)
Câu e:
\((+7) . (-5) = - (7.5) = -35\).
2. Giải bài 79 trang 91 SGK Toán 6 tập 1
Tính \(27 . (-5)\). Từ đó suy ra các kết quả:
\((+27) . (+5)\) \((-27) . (+5)\)
\((-27) . (-5) \) \( (+5) . (-27)\).
Phương pháp giải
- Muốn nhân hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu "-" trước kết quả nhận được.
- Muốn nhân hai số nguyên cùng dấu (cùng dấu âm), ta nhân hai giá trị tuyệt đối của chúng với nhau.
Hướng dẫn giải
\(27 . (-5) = - (27.5) = -135\)
Từ đó ta suy ra:
\((+27) . (+5) =27.5=135 \);
\((-27) . (+5)=-(27.5)=-135\);
\((-27) . (-5) =27.5= 135\);
\( (+5) . (-27)=-(5.27)=-135\).
3. Giải bài 80 trang 91 SGK Toán 6 tập 1
Cho a là một số nguyên âm. Hỏi b là số nguyên âm hay số nguyên dương nếu biết:
a) \(a . b\) là một số nguyên dương?
b) \(a . b\) là một số nguyên âm?
Phương pháp giải
Sử dụng:
- 1 số âm nhân 1 số âm thì kết quả ra 1 số dương (hay tích 2 số cùng dấu mang dấu dương)
- 1 số âm nhân 1 số dương thì kết quả ra 1 số âm (hay tích 2 số trái dấu mang dấu âm)
Hướng dẫn giải
Câu a:
Tích \( a . b\) là một số nguyên dương nên a và b cùng dấu.
Mà a là một số nguyên âm nên b cũng là số nguyên âm
Câu b:
Tích \(a . b\) là một số nguyên âm nên a và b trái dấu.
Mà a là một số nguyên âm nên b là số nguyên dương.
4. Giải bài 81 trang 91 SGK Toán 6 tập 1
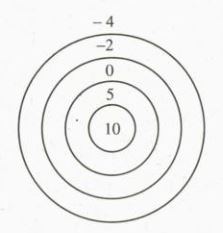
Trong trò chơi bắn bi vào các hình tròn vẽ trên mặt đất (h.52), bạn Sơn bắn được ba viên điểm 5, một viên điểm 0 và hai viên điểm -2; bạn Dũng bắn được hai viên điểm 10, một viên điểm -2 và ba viên điểm -4. Hỏi bạn nào được điểm cao hơn?
Phương pháp giải
- Tính tổng số điểm của bạn Sơn và tổng số điểm của bạn Dũng rồi so sánh.
- Sử dụng quy tắc nhân hai số nguyên và quy tắc cộng số nguyên để thực hiện phép tính.
Hướng dẫn giải
Bạn Sơn bắn được ba viên điểm 5, một viên điểm 0 và hai viên điểm -2
Do đó, tổng số điểm của bạn Sơn bắn được là:
\(3.5 + 1.0 + 2. (-2) \)\(= 15 + 0 - 4 = 11\) điểm
Bạn Dũng bắn được hai viên điểm 10, một viên điểm -2 và ba viên điểm -4
Do đó, tổng số điểm của bạn Dũng bắn được là:
\(2.10 + 1.(-2) + 3.(-4)\)\(=20 + (-2) + (-12)\)\( = 20 - 2 - 12 = 6\) điểm
Vì \(11 > 6\) nên bạn Sơn được điểm cao hơn bạn Dũng.
5. Giải bài 82 trang 92 SGK Toán 6 tập 1
So sánh:
a) (-7) . (-5) với 0;
b) (-17) . 5 với (-5) . (-2);
c) (+19) . (+6) với (-17) . (-10).
Phương pháp giải
Cách 1: Sử dụng nhận xét:
- Tích của 2 số nguyên cùng dấu thì kết quả là 1 số nguyên dương.
- Tích của hai số nguyên khác dấu kết quả là một số nguyên âm.
- Số nguyên âm < 0 < số nguyên dương.
Cách 2: Tính các tích rồi so sánh.
Hướng dẫn giải
Câu a:
Cách 1: Tích \((-7).(-5)\) là tích của hai số nguyên cùng dấu nên kết quả là số dương.
Do đó: \((-7).(-5) > 0\)
Cách 2: \( (-7).(-5) = 35 > 0\)
Câu b:
Cách 1: \((-17).5\) là tích của hai số nguyên khác dấu nên kết quả là số âm (<0)
\((-5).(-2)\) là tích của hai số nguyên cùng dấu nên kết quả là số dương (> 0)
Do đó: \((-17).5 < (-5).(-2)\)
Cách 2: \((-17).5 = - 85;\) \((-5).(-2) = 10\)
Vì \(-85 < 10\) nên \((-17).5 < (-5).(-2)\)
Câu c:
\((+19).(+6) = 114;\)
\((-17).(-10) = 170\)
Vì \(114 < 170\) nên \((+19).(+6) < (-17).(-10)\)
6. Giải bài 83 trang 92 SGK Toán 6 tập 1
Giá trị của biểu thức \((x - 2) . (x + 4)\) khi \(x = -1\) là số nào trong bốn đáp số A, B, C, D dưới đây:
A. \(9\); B. \(-9\);
C. \(5\); D. \(-5\).
Phương pháp giải
Thay \(x = -1\) vào biểu thức đã cho sau đó thực hiện phép tính để tìm ra kết quả.
Hướng dẫn giải
Thay giá trị của \(x\) trong biểu thức bởi \(-1,\) ta được:
\((x - 2) . (x + 4)=[(-1) - 2].[(-1) + 4] \)
\(= [- (1+2) ]. (4-1)= (-3).3 = - (3.3) = -9\)
Chọn B.
7. Giải bài 84 trang 92 SGK Toán 6 tập 1
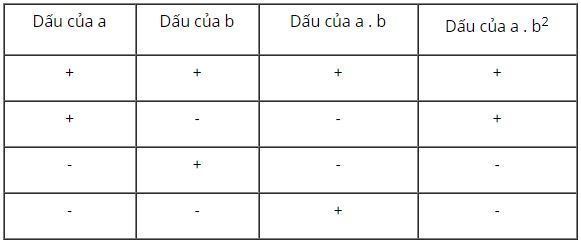
Điền các dấu “+”, “-“ thích hợp vào ô trống:
Phương pháp giải
Sử dụng các nhận xét sau:
- Tích của hai số nguyên trái dấu là 1 số âm
- Tích của hai số nguyên cùng dấu là 1 số dương.
- Bình phương của một số luôn dương.
Hướng dẫn giải
Ta có bảng sau:
Giải thích:
Ta có \(b^2\) luôn mang dấu + với mọi \(b\ne 0\). Nên dấu của \(a.b^2\) sẽ cùng dấu với dấu của \(a\).
Tích hai số cùng dấu là một số dương.
Tích hai số khác dấu là một số âm.
8. Giải bài 85 trang 92 SGK Toán 6 tập 1
Tính:
a) \((-25) . 8\); b) \(18 . (-15)\);
c) \((-1500) . (-100)\); d) \({\left( { - 13} \right)^2}\).
Phương pháp giải
Thực hiện phép tính nhân. Sử dụng:
- Tích của hai số nguyên cùng dấu là 1 số nguyên dương;
- Tích của hai số nguyên trái dấu là 1 số nguyên âm.
- Bình phương của một số luôn dương.
Hướng dẫn giải
Câu a:
\((-25) . 8 = - (25.8) = -200;\)
Câu b:
\(18 . (-15) = - (18. 15) = -270;\)
Câu c:
\((-1500) . (-100) = 1500 . 100\) \(= 150 000;\)
Câu d:
\((-13)^2= (-13). (-13)\)\(= 13. 13 = 169.\)
9. Giải bài 86 trang 92 SGK Toán 6 tập 1
Điền số vào ô trống cho đúng:
Phương pháp giải
- Muốn nhân hai số nguyên âm, ta nhân hai giá trị tuyệt đối của chúng.
- Muốn nhân hai số nguyên khác dấu ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu "−" trước kết quả.
- Tích của hai số nguyên cùng dấu là một số nguyên dương.
- Tích của hai số nguyên khác dấu là một số nguyên âm.
Hướng dẫn giải
\(a = –15; b = 6;\) \(a . b = (–15) . 6\)\( = – (15 . 6) = –90.\)
\(a . b = –39\) nên a và b trái dấu. Do đó b mang dấu \("–"\)
Mà \(39 = 13 . 3\) nên \(b = –3.\)
\(a . b = 28\) nên a và b cùng dấu. Do đó a mang dấu \("–"\)
Lại có \(28 = 7 . 4\) nên \(a = –4.\)
\(a . b = –36\) nên a và b trái dấu. Do đó b mang dấu \("–"\)
Mà \(36 = 9 . 4\) nên \(b = –4.\)
\(a . b = 8\) nên a và b cùng dấu. Do đó a mang dấu \("–"\)
Mà \(8 = 8 . 1\) nên \(a = –1. \)
10. Giải bài 87 trang 92 SGK Toán 6 tập 1
Biết rằng \(3^2= 9.\) Có còn số nguyên nào khác mà bình phương của nó cũng bằng 9 ?
Phương pháp giải
Sử dụng nhân hai số nguyên cùng dấu âm ta được một số dương.
Hướng dẫn giải
Còn số \(-3\) mà bình phương của nó bằng \(9\) vì: \((-3)^2= (-3). (-3) =3.3= 9.\)
11. Giải bài 88 trang 92 SGK Toán 6 tập 1
Cho x ∈ Z, so sánh: (-5) . x với 0.
Phương pháp giải
- Ta cần xét các trường hợp xảy ra với x, vì chưa biết x âm hay dương hay bằng 0
- Sử dụng:
- Tích hai số nguyên âm là một số nguyên dương
- Tích hai số nguyên trái dấu là một số nguyên âm
- Số nào nhân với 0 cũng bằng 0.
Hướng dẫn giải
Ta có \(-5\) là 1 số nguyên âm.
Nếu x < 0 nghĩa là x là số nguyên âm mà (-5) cũng là 1 số nguyên âm.
Do đó \((-5) . x > 0\) (tích hai số nguyên âm là một số nguyên dương)
Nếu x = 0 thì \((-5) . x=(-5).0 = 0.\)
Nếu x > 0 nghĩa là x là số nguyên dương hay x và (-5) trái dấu.
Do đó \((-5) . x < 0\) (tích hai số nguyên trái dấu là một số nguyên âm)
12. Giải bài 89 trang 92 SGK Toán 6 tập 1
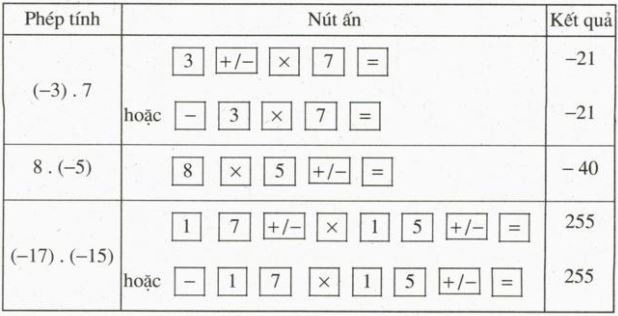
Sử dụng máy tính bỏ túi.
Dùng máy tính bỏ túi để tính:
a) \((-1356) . 17;\)
b) \(39 . (-152);\)
c) \((-1909) . (-75).\)
Hướng dẫn giải
Câu a:
\((-1356) . 17 = - 23052;\)
Câu b:
\(39 . (-152) = - 5928;\)
Câu c:
\((-1909) . (-75) = 143175.\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Làm quen với số nguyên âm
- doc Giải bài tập SGK Toán 6 Bài 2: Tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 3: Thứ tự trong tập hợp các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 4: Cộng hai số nguyên cùng dấu
- doc Giải bài tập SGK Toán 6 Bài 5: Cộng hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 6: Tính chất của phép cộng các số nguyên
- doc Giải bài tập SGK Toán 6 Bài 7: Phép trừ hai số nguyên
- doc Giải bài tập SGK Toán 6 Bài 8: Quy tắc dấu ngoặc
- doc Giải bài tập SGK Toán 6 Bài 9: Quy tắc chuyển vế
- doc Giải bài tập SGK Toán 6 Bài 10: Nhân hai số nguyên khác dấu
- doc Giải bài tập SGK Toán 6 Bài 12: Tính chất của phép nhân
- doc Giải bài tập SGK Toán 6 Bài 13: Bội và ước của một số nguyên
- doc Giải bài tập SGK Toán 6 Ôn tập chương 2: Số nguyên
.JPG)
.JPG)
.JPG)