Giải bài tập SGK Toán 6 Bài 11: Tính chất cơ bản của phép nhân phân số
Phần hướng dẫn giải bài tập SGK Tính chất cơ bản của phép nhân phân số sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập hai.
Mục lục nội dung
1. Giải bài 73 trang 39 SGK Toán 6 tập 2
2. Giải bài 74 trang 39 SGK Toán 6 tập 2
3. Giải bài 75 trang 39 SGK Toán 6 tập 2
4. Giải bài 76 trang 40 SGK Toán 6 tập 2
5. Giải bài 77 trang 40 SGK Toán 6 tập 2
6. Giải bài 78 trang 41 SGK Toán 6 tập 2
7. Giải bài 79 trang 41 SGK Toán 6 tập 2
8. Giải bài 80 trang 41 SGK Toán 6 tập 2
9. Giải bài 81 trang 41 SGK Toán 6 tập 2

1. Giải bài 73 trang 39 SGK Toán 6 tập 2
Trong hai câu sau đây, câu nào đúng?
Câu thứ nhất: Để nhân hai phân số cùng mẫu, ta nhân hai tử với nhau và giữ nguyên mẫu.
Câu thứ hai: Tích của hai phân số bất kì là một phân số có tử là tích của hai tử và mẫu là tích của hai mẫu.
Phương pháp giải
Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\) (với \(b,d \ne 0\))
Hướng dẫn giải
Câu thứ nhất sai. Câu thứ hai đúng.
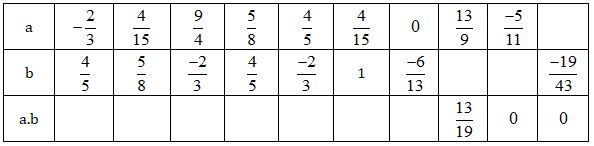
2. Giải bài 74 trang 39 SGK Toán 6 tập 2
Điền các số thích hợp vào bảng sau:
Phương pháp giải
- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\)
- Mọi số nhân với 0 thì đều bằng 0.
- Mọi số nhân với 1 thì đều bằng chính nó.
Hướng dẫn giải
3. Giải bài 75 trang 39 SGK Toán 6 tập 2
Hoàn thành bảng nhân sau (chú ý rút ngắn gọn nếu có thể) :
Phương pháp giải
- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\)
- Lấy lần lượt từng thừa số ở cột rồi nhân lần lượt với từng thừa số ở hàng, sau đó rút gọn rồi điền kết quả vào ô tương ứng.
Hướng dẫn giải
Các phép nhân ở hàng 2 là:
\(\dfrac{2}{3}.\dfrac{{ - 5}}{6} = \dfrac{{2.\left( { - 5} \right)}}{{3.6}} \)\(= \dfrac{{1.\left( { - 5} \right)}}{{3.3}} = \dfrac{{ - 5}}{9}\)
\(\begin{array}{l}
\,\dfrac{2}{3}.\dfrac{7}{{12}} = \dfrac{{2.7}}{{3.12}} = \dfrac{{1.7}}{{3.6}} = \dfrac{7}{{18}}\\
\,\dfrac{2}{3}.\dfrac{{ - 1}}{{24}} = \dfrac{{2.\left( { - 1} \right)}}{{3.24}} = \dfrac{{1.\left( { - 1} \right)}}{{3.8}} = \dfrac{{ - 1}}{{24}}
\end{array}\)
Thực hiện tương tự với các hàng tiếp theo ta có bảng kết quả sau khi đã rút gọn:
4. Giải bài 76 trang 40 SGK Toán 6 tập 2
Tính giá trị biểu thức sau một cách hợp lí:
\(A=\dfrac{7}{19}.\dfrac{8}{11}+\dfrac{7}{19}.\dfrac{3}{11}+\dfrac{12}{19}\) ;
\(B= \dfrac{5}{9}.\dfrac{7}{13}+\dfrac{5}{9}.\dfrac{9}{13}-\dfrac{5}{9}.\dfrac{3}{13}\) ;
\(C=\left (\dfrac{67}{111}+\dfrac{2}{33}-\dfrac{15}{117} \right ).\left (\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12} \right )\).
Phương pháp giải
- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\)
- Sử dụng các tính chất cơ bản của phép nhân phân số:
- Tính chất giao hoán: \(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{c}{d}.\dfrac{a}{b}\)
- Tính chất kết hợp: \(\left( {\dfrac{a}{b}.\dfrac{c}{d}} \right).\dfrac{p}{q} = \dfrac{a}{b}.\left( {\dfrac{c}{d}.\dfrac{p}{q}} \right)\)
- Nhân với số 1: \(\dfrac{a}{b}.1 = 1.\dfrac{a}{b} = \dfrac{a}{b}\)
- Tính chất phân phối của phép nhân đối với phép cộng: \(\dfrac{a}{b}.\left( {\dfrac{c}{d} + \dfrac{p}{q}} \right) = \dfrac{a}{b}.\dfrac{c}{d} + \dfrac{a}{b}.\dfrac{p}{q}\)
Hướng dẫn giải
\(A=\dfrac{7}{19}.\dfrac{8}{11}+\dfrac{7}{19}.\dfrac{3}{11}+\dfrac{12}{19}\)
\(A= \dfrac{7}{19}.\left (\dfrac{8}{11}+\dfrac{3}{11} \right )+\dfrac{12}{19}\)
\(A = \dfrac{7}{{19}}.\dfrac{{11}}{{11}} + \dfrac{{12}}{{19}}\)
\(A=\dfrac{7}{19}.1 +\dfrac{12}{19}\)
\(A=\dfrac{7+12}{19} \)
\(A=\dfrac{19}{19}=1\)
\(B= \dfrac{5}{9}.\dfrac{7}{13}+\dfrac{5}{9}.\dfrac{9}{13}-\dfrac{5}{9}.\dfrac{3}{13}\)
\(B=\dfrac{5}{9}.\left (\dfrac{7}{13}+\dfrac{9}{13}-\dfrac{3}{13} \right )\)
\(B=\dfrac{5}{9}.\dfrac{7+9-3}{13}\)
\(B=\dfrac{5}{9}.\dfrac{13}{13}=\dfrac{5}{9}.1=\dfrac{5}{9}\)
\(C=\left (\dfrac{67}{111}+\dfrac{2}{33}-\dfrac{15}{117} \right ).\left (\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12} \right )\)
\(C=\left (\dfrac{67}{111}+\dfrac{2}{33}-\dfrac{15}{117} \right ).\dfrac{4-3-1}{12}\)
\(C=\left (\dfrac{67}{111}+\dfrac{2}{33}-\dfrac{15}{117} \right ).0=0\)
5. Giải bài 77 trang 40 SGK Toán 6 tập 2
Tính giá trị các biểu thức sau:
\(A=a.\dfrac{1}{2} +a.\dfrac{1}{3}-a.\dfrac{1}{4}\) với \(a= \dfrac{-4}{5}\);
\(B=\dfrac{3}{4}.b+\dfrac{4}{3}.b-\dfrac{1}{2}.b\) với \(b=\dfrac{6}{19}\) ;
\(C=c.\dfrac{3}{4}+c.\dfrac{5}{6}-c.\dfrac{19}{12}\) với \(c=\dfrac{2002}{2003}\) ;
Phương pháp giải
- Sử dụng tính chất phân phối của phép nhân đối với phép cộng: \(\dfrac{a}{b}.\left( {\dfrac{c}{d} + \dfrac{p}{q}} \right) = \dfrac{a}{b}.\dfrac{c}{d} + \dfrac{a}{b}.\dfrac{p}{q}\) để thu gọn biểu thức rồi mới thay giá trị cụ thể của biến vào và thực hiện phép nhân phân số.
- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\)
Hướng dẫn giải
Ta có:
\(A=a.\left (\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{4} \right )\)
\(=a.\dfrac{6+4-3}{12}=a.\dfrac{7}{12}\)
Với \(a= \dfrac{-4}{5}\) , thì \(A=\dfrac{-4}{5}.\dfrac{7}{12}=\dfrac{-7}{15}.\)
\(B=\dfrac{3}{4}.b+\dfrac{4}{3}.b-\dfrac{1}{2}.b\)
\(=b.\left( {\dfrac{3}{4} + \dfrac{4}{3} - \dfrac{1}{2}} \right) \)
\(= b.\dfrac{{3.3 + 4.4 - 1.6}}{{12}} = b.\dfrac{{19}}{{12}}\)
Với \(b = \dfrac{6}{{19}} \Rightarrow B = \dfrac{6}{{19}}.\dfrac{{19}}{{12}}\)\( = \dfrac{1}{2}\)
Vậy \(B=\dfrac{1}{2}\)
\(C = c.\left( {\dfrac{3}{4} + \dfrac{5}{6} - \dfrac{{19}}{{12}}} \right) \)
\(= c.\left( {\dfrac{{3.3}}{{12}} + \dfrac{{5.2}}{{12}} - \dfrac{{19}}{{12}}} \right) \)
\(= c.0 = 0\)
Hay \(C = 0\) vói mọi \(c\)
Vậy với \(c=\dfrac{2002}{2003}\) thì \(C=0.\)
6. Giải bài 78 trang 41 SGK Toán 6 tập 2
Căn cứ vào tính chất giao hoán và tính chất kết hợp của phép nhân số nguyên ta có thể suy ra tính chất giao hoán và tính chất kết hợp của phép nhân phân số.
Ví dụ: Tính chất giao hoán của phép nhân phân số:
\(\displaystyle {a \over b}.{c \over d} = {{a.c} \over {b.d}} = {{c.a} \over {d.b}} = {c \over d}.{a \over b}\)
Bằng cách tương tự, em hãy suy ra tính chất kết hợp của phép nhân phân số từ tính chất kết hợp của phép nhân số nguyên
Phương pháp giải
- Viết tương tự như tính chất kết hợp của phép nhân số nguyên, ta chỉ thay số nguyên thành phân số.
- Tính chất kết hợp của phép nhân số nguyên là: \((a.b).c = a.(b.c)\).
Hướng dẫn giải
Tính chất kết hợp của phép nhân phân số:
\(\left(\dfrac{a}{b}.\dfrac{c}{d}\right).\dfrac{p}{q}\)\(= \dfrac{a}{b}.\left( {\dfrac{c}{d}.\dfrac{p}{q}} \right)\)
7. Giải bài 79 trang 41 SGK Toán 6 tập 2
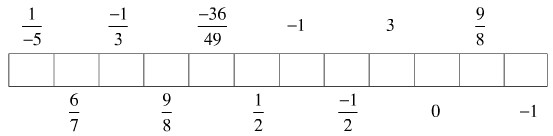
Em hãy tính các tích sau rồi viết chữ tương ứng với đáp số đúng vào các ô trống. Khi đó em sẽ biết được tên của một nhà toán học Việt Nam nổi tiếng ở thế kỉ XV.
T. \( \displaystyle {{ - 2} \over 3}.{{ - 3} \over 4}\)
U. \( \displaystyle {6 \over 7}.1\)
E. \( \displaystyle {{16} \over {17}}.{{ - 17} \over {32}}\)
H. \( \displaystyle {{13} \over {19}}.{{ - 19} \over {13}}\)
G. \( \displaystyle {{15} \over {49}}.{{ - 84} \over {35}}\)
O. \( \displaystyle {1 \over 2}.{3 \over 4}.{{ - 8} \over 9}\)
N. \( \displaystyle {{ - 5} \over {16}}.{{ - 18} \over 5}\)
I.\( \displaystyle {6 \over {11}}.{{ - 1} \over 7}.0.{3 \over {29}}\)
V. \( \displaystyle {7 \over 6}.{{36} \over {14}}\)
L. \( \displaystyle {3 \over { - 5}}.{1 \over 3}\)
Phương pháp giải
Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\)
Hướng dẫn giải
T. \( \displaystyle {{ - 2} \over 3}.{{ - 3} \over 4}\) = \( \displaystyle {1 \over 2}\)
U. \( \displaystyle {6 \over 7}.1\) = \( \displaystyle {6 \over 7}\)
E. \( \displaystyle {{16} \over {17}}.{{ - 17} \over {32}}\) = \( \displaystyle - {1 \over 2}\)
H. \( \displaystyle {{13} \over {19}}.{{ - 19} \over {13}}=-1\)
G. \( \displaystyle {{15} \over {49}}.{{ - 84} \over {35}}\) = \( \displaystyle - {{36} \over {49}}\)
O. \( \displaystyle {1 \over 2}.{3 \over 4}.{{ - 8} \over 9}\) = \( \displaystyle - {1 \over 3}\)
N. \( \displaystyle {{ - 5} \over {16}}.{{ - 18} \over 5}\) = \( \displaystyle {9 \over 8}\)
I.\( \displaystyle {6 \over {11}}.{{ - 1} \over 7}.0.{3 \over {29}}=0\)
V. \( \displaystyle {7 \over 6}.{{36} \over {14}}=3\)
L. \( \displaystyle {3 \over { - 5}}.{1 \over 3}\) = \( \displaystyle - {1 \over 5}\)
Ta tìm được nhà Toán học Việt Nam nổi tiếng ở thế kỉ XV là Lương Thế Vinh.
8. Giải bài 80 trang 41 SGK Toán 6 tập 2
Tính:
a) \( \displaystyle 5.{{ - 3} \over {10}}\)
b) \( \displaystyle {2 \over 7} + {5 \over 7}.{{14} \over {25}}\)
c) \( \displaystyle {1 \over 3} - {5 \over 4}.{4 \over {15}}\)
d) \( \displaystyle \left( {{3 \over 4} + {{ - 7} \over 2}} \right).\left( {{2 \over {11}} + {{12} \over {22}}} \right)\)
Phương pháp giải
- Trong biểu thức có các phép cộng, trừ, nhân thì thực hiện phép nhân trước.
- Trong biểu thức có dấu ngoặc thì thức hiện phép tính trong ngoặc trước.
- Muốn nhân hai phân số, ta nhân các tử với nhau và nhân các mẫu với nhau:
\(\dfrac{a}{b}.\dfrac{c}{d} = \dfrac{{a.c}}{{b.d}}\)
Hướng dẫn giải
Câu a:
\(\,\,5.\dfrac{{ - 3}}{{10}} = \dfrac{{ 5.(- 3)}}{10}= \dfrac{{ - 3}}{2}\)
Câu b:
\(\,\,\dfrac{2}{7} + \dfrac{5}{7}.\dfrac{{14}}{{25}} = \dfrac{2}{7} + \dfrac{{5.14}}{{7.25}} \\= \dfrac{2}{7} + \dfrac{2}{5} = \dfrac{{10}}{{35}} + \dfrac{{14}}{{35}} = \dfrac{{24}}{{35}}\\\)
Câu c:
\(\,\dfrac{1}{3} - \dfrac{5}{4}.\dfrac{4}{{15}} = \dfrac{1}{3} - \dfrac{5.4}{4.15}= \dfrac{1}{3} - \dfrac{1}{3} = 0\\\)
Câu d:
\(\,\,\left( {\dfrac{3}{4} + \dfrac{{ - 7}}{2}} \right).\left( {\dfrac{2}{{11}} + \dfrac{{12}}{{22}}} \right)\\ = \left( {\dfrac{3}{4} + \dfrac{{ - 14}}{4}} \right).\left( {\dfrac{4}{{22}} + \dfrac{{12}}{{22}}} \right) \\= \dfrac{{ - 11}}{4}.\dfrac{{16}}{{22}} = \dfrac{{ - 11.16}}{4.22}= - 2 \)
Đáp số: \(\displaystyle a){{ - 3} \over 2};b){{24} \over {35}}\) ; \(c)\,\,0; d) \,\,-2.\)
9. Giải bài 81 trang 41 SGK Toán 6 tập 2
Tính diện tích và chu vi một khu đất hình chữ nhật có chiều dài \(\dfrac{1}{4}\) km và chiều rộng \(\dfrac{1}{8}\) km
Phương pháp giải
Diện tích hình chữ nhật là chiều dài nhân chiều rộng.
Chu vi hình chữ nhật là (chiều dài + chiều rộng) x 2
Hướng dẫn giải
Diện tích khu đất hình chữ nhật là:
\( \displaystyle {1 \over 4} . {1 \over 8} = {1 \over {32}}\) (km2)
Chu vi khu đất hình chữ nhật là:
\( \displaystyle \left( {{1 \over 4} + {1 \over 8}} \right) .2 =2.{3 \over 8}= {3 \over 4}\) (km)
10. Giải bài 82 trang 41 SGK Toán 6 tập 2
Đoán vui: Một con ong và bạn Dũng cùng xuất phát từ A đến B. Biết rằng mỗi giây ong bay được 5m và mỗi giờ Dũng đạp xe đi được 12 km. Hỏi con ong hay bạn Dũng đến B trước?
Phương pháp giải
- Vì con ong và bạn Dũng cùng đi trên một quãng đường nên vận tốc nào lớn hơn (nhanh hơn) thì sẽ đến B sớm hơn.
- Ta đổi hai đại lượng về cùng một đơn vị rồi so sánh.
Hướng dẫn giải
Cách 1:
Đổi vận tốc của bạn Dũng từ km/h sang m/s
1km = 1000 m; 1h = 3600 giây.
\(1\dfrac{{km}}{h} = \dfrac{{1000m}}{{3600s}} = \dfrac{5}{{18}}m/s\)
Vận tốc của Dũng:
\(12\dfrac{{km}}{h} = 12.\dfrac{5}{{18}}\dfrac{m}{s} \)
\(= \dfrac{{10}}{3}\)m\s < 5m\s = vận tốc của con ong.
Vận tốc của con ong lớn hơn bạn Dũng.
Vậy: con ong sẽ đến B trước bạn Dũng.
11. Giải bài 83 trang 41 SGK Toán 6 tập 2
Lúc 6 giờ 50 phút bạn Việt đi xe đạp từ A để đến B với vận tốc 15 km/h. Lúc 7 giờ 10 phút bạn Nam đi xe đạp từ B đến A với vận tốc 12 km/h. Hai bạn gặp nhau ở C lúc 7 giờ 30 phút. Tính quãng đường AB.
Phương pháp giải
- Sử dụng: quãng đường = vận tốc x thời gian
- Tìm thời gian mỗi bạn đi.
- Tìm quãng đường mỗi bạn đi được.
- Quãng đường AB chính bằng tổng quãng đường hai bạn đi được.
Hướng dẫn giải

Cho đến lúc hai bạn gặp nhau, thời gian bạn Việt đã đi là:
7 giờ 30 phút – 6 giờ 50 phút = 40 phút \(= \displaystyle {2 \over 3}\) giờ.
Thời gian bạn Nam đã đi đến khi gặp nhau là:
7 giờ 30 phút – 7 giờ 10 phút = 20 phút \( =\displaystyle {1 \over 3}\) giờ.
Quãng đường bạn Việt đã đi là: \( \displaystyle 15.{2 \over 3} = 10\left( {km} \right)\).
Quãng đường bạn Nam đã đi là: \( \displaystyle 12.{1 \over 3} = 4\left( {km} \right)\)
Vì tổng hai quãng đường mà hai bạn đã đi bằng quãng đường AB nên
\(AB = 10 + 4 = 14\) (km)
Đáp số: Quãng đường AB dài 14 km.
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Mở rộng khái niệm về phân số
- doc Giải bài tập SGK Toán 6 Bài 2: Phân số bằng nhau
- doc Giải bài tập SGK Toán 6 Bài 3: Tính chất cơ bản của phân số
- doc Giải bài tập SGK Toán 6 Bài 4: Rút gọn phân số
- doc Giải bài tập SGK Toán 6 Bài 5: Quy đồng mẫu số nhiều phân số
- doc Giải bài tập SGK Toán 6 Bài 6: So sánh phân số
- doc Giải bài tập SGK Toán 6 Bài 7: Phép cộng phân số
- doc Giải bài tập SGK Toán 6 Bài 8: Tính chất cơ bản của phép cộng phân số
- doc Giải bài tập SGK Toán 6 Bài 9: Phép trừ phân số
- doc Giải bài tập SGK Toán 6 Bài 10: Phép nhân phân số
- doc Giải bài tập SGK Toán 6 Bài 12: Phép chia phân số
- doc Giải bài tập SGK Toán 6 Bài 13: Hỗn số. Số thập phân. Phần trăm
- doc Giải bài tập SGK Toán 6 Bài 14: Tìm giá trị phân số của một số cho trước
- doc Giải bài tập SGK Toán 6 Bài 15: Tìm một số biết giá trị một phân số của nó
- doc Giải bài tập SGK Toán 6 Bài 16: Tìm tỉ số của hai số
- doc Giải bài tập SGK Toán 6 Bài 17: Biểu đồ phần trăm
- doc Giải bài tập SGK Toán 6 Ôn tập Chương 3: Phân số
- doc Giải bài tập SGK Toán 6 Ôn tập cuối năm
.JPG)
.JPG)
.JPG)

