Giải bài tập SGK Toán 7 Bài 6: Tia phân giác của góc

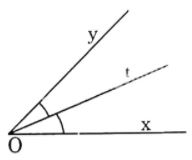
Trên cùng một nửa mặt phẳng chứa bờ \(Ox,\) vẽ tia Ot sao cho góc  \(\widehat{xOt}=25^0,\) \(\widehat{xOy}=50^0\) 

a) Tia \(Ot\) có nằm giữa hai tia \(Ox\) và \(Oy\) không?

b) So sánh góc \(tOy\) và góc \(xOt.\)

c ) Tia \(Ot\) có là tia phân giác của góc \(xOy\) không? Vì sao?

Hướng dẫn giải

Câu a:

Trên cùng một nửa mặt phẳng bờ chứa tia \(Ox\) có  \(\widehat{xOt}<\widehat{xOy}\) (vì \(25^0<50^0)\) nên tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\) (1)

Câu b:

Vì tia \(Ot\) nằm giữa hai tia \(Ox,Oy\) nên:

\(\widehat{xOt}\)\(+\widehat{yOt}\)= \(\widehat{xOy}\)                 

Thay số ta được: \(25^0+ \widehat{tOy}=50^0\)

Suy ra  \(\widehat{tOy}=50^0-25^0=25^0\)

Vậy \(\widehat{xOt}=\widehat{tOy}\,(=25^0)\)  (2)

Câu c:

Từ (1) và (2) ta có: Tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\) và  \(\widehat{xOt}=\widehat{tOy}\) nên \(Ot\) là tia phân giác của góc  \(xOy.\)

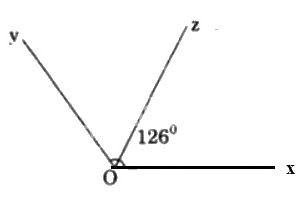
a) Vẽ góc \(xOy\) có số đo \(126^0\) 

b) Vẽ tia phân giác của góc \(xOy\) ở câu a.

Hướng dẫn giải

Câu a:

Dùng thước đo góc ta vẽ được góc \(xOy = 126^0\)

Cách vẽ:

- Vẽ tia \(Ox\)

- Đặt thước đo góc sao cho tâm của thước trùng với gốc \(O\) của tia \(Ox\) và tia \(Ox\) đi qua vạch \(0\) của thước.

- Kẻ tia \(Oy\) đi qua vạch \(126\) độ của thước đo góc. Vậy ta được góc \(xOy=126^0\) thỏa mãn yêu cầu bài toán.

Câu b:

Vì tia \(Oz\) là tia phân giác của góc \(xOy\) 

Nên \(\widehat{xOz}\) = \(\widehat{ zOy}\) = \(\dfrac{\widehat{xOy}}2\)\(=\dfrac{126^0}{2}=63^0\)

Cách vẽ: 

- Đặt thước đo góc trên nửa mặt phẳng (cùng phía với tia \(Oy\)) bờ là đường thẳng chứa tia \(Ox\) sao cho tâm của thước trùng với đỉnh \(O\) của góc \(xOy\) và tia \(Ox\) đi qua vạch \(0\) của thước .

- Kẻ tia \(Oz\) đi qua vạch \(63\) độ của thước thì \(Oz\) chính là tia phân giác của góc \(xOy.\) 

 Khi nào ta kết luận được tia \(Ot\) là tia phân giác của góc \(xOy\)? Trong những câu trả lời sau, em hãy chọn những câu đúng:

a)  \(\widehat{xOt}\) = \(\widehat{yOt}\)

b)\(\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\)

c) \(\widehat{xOt}\)\(+\widehat{tOy}\) \(=\widehat{xOy}\) và \(\widehat{xOt}\) \(=\widehat{yOt}\) 

d) \(\widehat{xOt}\)\(=\widehat{yOt}\) \(=\dfrac{1}2\widehat{xOy}\)

Hướng dẫn giải

Câu a:

Sai vì thiếu \(Ot\) nằm giữa \(Ox\) và \(Oy\)

Câu b:

Sai vì thiếu \(\widehat{xOt}\) = \(\widehat{yOt}\)

Câu c:

Đúng

Vì \(\widehat{xOt}\)\(+\widehat{tOy}\) \(=\widehat{xOy}\) ta suy ra tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\)

Lại có \(\widehat{xOt}\) \(=\widehat{yOt}\) nên tia \(Ot\) là tia phân giác của góc \(xOy\) 

d) Đúng

Vì \(\widehat{xOt}\)\(=\widehat{yOt}\) \(=\dfrac{1}2\widehat{xOy}\)

Nên \(\widehat{xOt}\)\(+\widehat{yOt}\) \(=\dfrac{1}2\widehat{xOy}+\dfrac{1}2\widehat{xOy}=\widehat{xOy}\) 

Hay \(\widehat{xOt}\)\(+\widehat{yOt}=\widehat{xOy}\) nên tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\)

Lại có \(\widehat{xOt}\) \(=\widehat{yOt}\) nên tia \(Ot\) là tia phân giác của góc \(xOy\)  

Vẽ hai góc kề bù \(xOy, yOx',\) biết \(\widehat{xOy}=130^0\). Gọi \(Ot\) là tia phân giác của góc \(xOy.\) Tính số đo góc \(\widehat{x'Ot}\).

Hướng dẫn giải

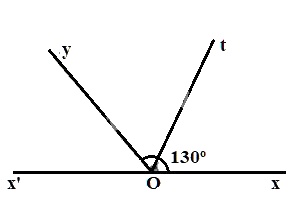
Vì \(Ot\) là tia phân giác của góc \(xOy\) nên:

\(\widehat{xOt} = \widehat {tOy} \)\(= \dfrac{1}2\widehat{xOy}\) \(=\dfrac{130^{0}}2=65^0\)

Vì hai góc \(xOy, yOx'\) kề bù nên \( \widehat {xOy} + \widehat {yOx'} = {180^0}=\widehat {xOx'}\)

Trên cùng một nửa mặt phẳng có bờ là đường thẳng \(xx'\), ta có \(\widehat {xOt}<\widehat {xOx'} \,\,({65^0}<{180^0} )\) nên tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Ox'\) 

Do đó:  

\(\widehat {xOt} + \widehat {x'Ot} = \widehat {xOx'} \)
\(\Rightarrow \widehat {x'Ot} = \widehat {xOx'} - \widehat {xOt} \)\(= {180^0} - {65^0} = {115^0} \)

Vẽ hai góc kề bù \(xOy\) và \(yOx',\) biết \(\widehat{xOy}=100^0\) . Gọi \(Ot\) là tia phân giác của góc \(xOy\) và \(Ot'\) là tia phân giác của góc \(x'Oy.\) Tính số đo các góc \(x'Ot, xOt', tOt'.\) 

Hướng dẫn giải

Hai góc \(xOy\) và \(x'Oy\) là hai góc kề bù nên \(\widehat{xOy}+\widehat{x'Oy}=180^0\) mà \(\widehat{xOy}=100^0\) nên \(\widehat{x'Oy}=180^0-\widehat{xOy}\)\(=180^0-100^0=80^0\) 

Vì \(Ot\) là tia phân giác của góc \(xOy\) nên \(\displaystyle \widehat {xOt} = \widehat {tOy} = {{\widehat {xOy}} \over 2}\)\( \displaystyle = {{{{100}^0}} \over 2} = {50^0}\)

Vì \(Ot'\) là tia phân giác của góc \(x'Oy\) nên \(\displaystyle \widehat {x'Ot'} = \widehat {t'Oy} \)\(\displaystyle = {{\widehat {x'Oy}} \over 2} = {{{{80}^0}} \over 2} = {40^0}\)

- Góc \(x'Ot\) và góc \(xOt\) là hai góc kề bù nên \(\widehat {x'Ot} + \widehat {xOt}=180^0\)

Suy ra \(\widehat {x'Ot}=180^0-\widehat {xOt}=180^0-50^0=130^0\)

- Góc \(xOt'\) và góc \(x'Ot'\) là hai góc kề bù nên \(\widehat {xOt'} + \widehat {x'Ot'}=180^0\)

Suy ra \(\widehat {xOt'}=180^0-\widehat {x'Ot'}=180^0-40^0=140^0\)

- Vì tia \(Ot'\) nằm giữa hai tia \(Ox'\) và \(Oy,\) tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\)

Lại có hai góc \(xOy\) và \(x'Oy\) là hai góc kề bù nên tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ox'\)

Suy ra tia \(Oy\) nằm giữa hai tia \(Ot\) và \(Ot'\)

Do đó \(\widehat {yOt'} + \widehat {yOt}=\widehat {t'Ot}\)

Suy ra \(\widehat {t'Ot}=50^0+40^0=90^0\)

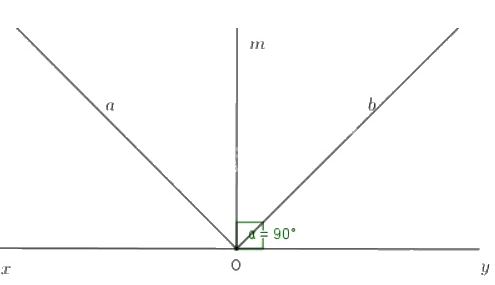
Vẽ góc bẹt \(xOy.\) Vẽ tia phân giác \(Om\) của góc đó. Vẽ tia phân giác \(Oa\) của góc \(xOm.\) Vẽ tia phân giác \(Ob\) của góc \(mOy.\) Tính số đo góc \(aOb.\) 

Hướng dẫn giải

Tia \(Oa\) là tia phân giác của góc \(xOm\) nên \(\widehat{ aOm}=\dfrac{\widehat{xOm}}2\)

Tia \(Ob\) là tia phân giác của góc \(yOm\) nên \(\widehat{bOm}=\dfrac{\widehat{yOm}}2\).

Tia  \(Om\) nằm giữa hai tia \(Oa, Ob\) do đó: \(\widehat{aOb}\)= \(\widehat{aOm}+\widehat{bOm}\) 

\( = \dfrac{1}{2}\left( {\widehat {xOm} + \widehat {yOm}} \right) = \dfrac{1}{2}\widehat {xOy}\)

\( = \dfrac{1}{2}.180^\circ  = 90^\circ \)

Cho hai tia \(Oy,Oz\) cùng nằm trên một nửa mặt phẳng có bờ chứa tia \(Ox.\) Biết: \(\widehat{ xOy}=30^0,\) \(\widehat{ xOz}=80^0.\) Vẽ tia phân giác \(Om\) của \(\widehat {xOy}\). Vẽ tia phân giác \(On\) của \(\widehat {yOz}\). Tính \(\widehat {mOn}\) 

Hướng dẫn giải

Vì hai tia \(Oy, Oz\) cùng nằm trên nửa mặt phẳng bờ chứa tia \(Ox\) mà 

\(\widehat{ xOy}\)<  \(\widehat{ xOz}\) \((30^0<80^0)\) nên tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\)

Do đó  \(\widehat{ xOy}\)+ \(\widehat{ yOz}\)= \(\widehat{ xOz}\)  

Suy ra  \(\widehat{ yOz}=\widehat{ xOz}-\widehat{ xOy}\)\(= 80^0-30^0=50^0\) 

Ta có tia \(Om\) là tia phân giác của góc \(xOy\) nên: \(\widehat {xOm} = \widehat {mOy} \)\(= \dfrac{{\widehat {xOy}}}{2} = \dfrac{{{{30}^0}}}{2} = {15^0}\)

Tia \(On\) là tia phân giác của góc \(yOz\) nên: \(\widehat {yOn} = \widehat {nOz} = \dfrac{{\widehat {yOz}}}{2} \)\(= \dfrac{{{{50}^0}}}{2} = {25^0}\)

Vì tia \(Oy\) nằm giữa hai tia \(Ox,Oz\) mà tia \(On\) là tia phân giác góc \(zOy\), tia \(Om\) là tia phân giác góc \(xOy\) nên \(Om\) và \(On\) nằm trên hai nửa mặt phẳng đối nhau bờ là tia \(Oy\). Do đó tia \(Oy\) nằm giữa hai tia \(Om, On\), suy ra: 

\(\widehat{mOn}\) =\(\widehat{mOy}\) + \(\widehat{yOn}\) \( = {15^0} + {25^0} = {40^0}\)

Cho hai tia \(Oy, Oz\) cùng nằm trên một nửa mặt phẳng có bờ chứa tia \(Ox.\) Biết rằng \(\widehat{xOy}=30^0\) , \(\widehat{xOz}=120^0.\)

a) Tính số đo góc \(yOz.\) 

b) Vẽ tia phân giác \(Om\) của \(\widehat{xOy}\), tia phân giác \(On\) của \(\widehat{xOz}\). Tính số đo góc \(mOn.\)

Hướng dẫn giải

Câu a:

Do hai tia \(Oy, Oz\) cùng nằm trên một nửa mặt phẳng bờ chứa tia \(Ox,\) mà: \(\widehat {xOy} < \widehat {xOz}\) \((30^0<120^0)\) nên ta có tia \(Oy\) nằm giữa hai tia \(Ox, Oz,\) từ đó ta có:

\(\widehat {xOy} + \widehat {yOz} = \widehat {xOz} \)\(\Rightarrow \widehat {yOz} = \widehat {xOz} - \widehat {xOy}\) 

\(\widehat{yOz}=120^0-30^0=90^0\)

Câu b:

Ta có tia \(Om\) là tia phân giác của góc \(xOy\) nên:

\(\widehat {xOm} = \widehat {yOm} = \dfrac{{\widehat {xOy}}}{2} \)\(= \dfrac{{{{30}^0}}}{2} = {15^0}\)

Ta có tia \(On\) là tia phân giác của góc \(xOz\) nên ta có:

\(\widehat {xOn} = \widehat {nOz} = \dfrac{{\widehat {xOz}}}{2} \)\(= \dfrac{{{{120}^0}}}{2} = {60^0}\)

Do hai tia \(Om, On\) cùng nằm trên một nửa mặt phẳng bờ chứa tia \(Ox,\) mà: \(\widehat {xOm} < \widehat {xOn}\) \((15^0<60^0)\) nên ta có tia \(Om\) nằm giữa hai tia \(Ox, On,\) từ đó ta có:

\(\widehat {xOm} + \widehat {mOn} = \widehat {xOn}\)

\(\Rightarrow \widehat {mOn} = \widehat {xOn} - \widehat {xOm} \)\(= {60^0} - {15^0} = {45^0}\)