Giải bài tập SGK Toán 6 Bài 7: Lũy thừa với số mũ tự nhiên và nhân hai lũy thừa cùng cơ số
Phần hướng dẫn giải bài tập Lũy thừa với số mũ tự nhiên và nhân hai lũy thừa cùng cơ số sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Toán 6 tập 1
Mục lục nội dung
1. Giải bài 56 trang 27 SGK Toán 6 tập 1
2. Giải bài 57 trang 28 SGK Toán 6 tập 1
3. Giải bài 58 trang 28 SGK Toán 6 tập 1
4. Giải bài 59 trang 28 SGK Toán 6 tập 1
5. Giải bài 60 trang 28 SGK Toán 6 tập 1
6. Giải bài 61 trang 28 SGK Toán 6 tập 1
7. Giải bài 62 trang 28 SGK Toán 6 tập 1
8. Giải bài 63 trang 28 SGK Toán 6 tập 1
9. Giải bài 64 trang 29 SGK Toán 6 tập 1

Giải bài tập SGK Toán 6 Bài 7: Lũy thừa với số mũ tự nhiên và nhân hai lũy thừa cùng cơ số
1. Giải bài 56 trang 27 SGK Toán 6 tập 1
Viết gọn các tích sau bằng cách dùng lũy thừa:
a) 5.5.5.5.5.5
b) 6.6.6.3.2
c) 2.2.2.3.3
d) 100.10.10.10
Phương pháp giải
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a: an=a.a.....a⏟n thừa số(n≠0)
Hướng dẫn giải
Câu a: 5.5.5.5.5.5=56
Câu b: 6.6.6.3.2=6.6.6.6=64
Câu c: 2.2.2.3.3=23.32
Câu d: 100.10.10.10=(10.10).10.10.10=105
Hoặc 100.10.10.10=100.103=102.103=102+3=105
2. Giải bài 57 trang 28 SGK Toán 6 tập 1
Tính giá trị các lũy thừa sau
a) 23,24,25,26,27,28,29,210;
b) 32,33,34,35;
c) 42,43,44;
d) 52,53,54;
e) 62,63,64
Phương pháp giải
Lũy thừa bậc n của a là tích của n thừa số bằng nhau, mỗi thừa số bằng a: an=a.a.....a⏟n thừa số(n≠0)
Hướng dẫn giải
Câu a: 23=2.2.2=8
24=23.2=8.2=16
25=24.2=16.2=32
26=25.2=32.2=64
27=26.2=64.2=128
28=27.2=128.2=256
29=28.2=256.2=512
210=29.2=512.2=1024
Câu b: 32=3.3=9
33=32.3=9.3=27
34=33.3=27.3=81
35=34.3=81.3=243
Câu c: 42=4.4=16
43=42.4=16.4=64
44=43.4=64.4=256
Câu d: 52=5.5=25
53=52.5=25.5=125
54=53.5=125.5=625
Câu e: 62=6.6=36
63=62.6=36.6=216
64=63.6=216.6=1296
3. Giải bài 58 trang 28 SGK Toán 6 tập 1
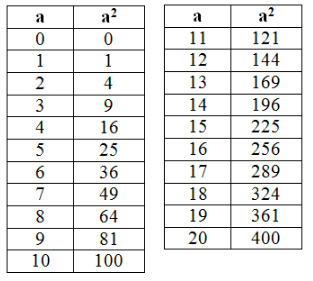
a) Lập bảng bình phương của các số tự nhiên từ 0 đến 20.
b) Viết mỗi số sau thành bình phương của một số tự nhiên: 64; 169; 196.
Phương pháp giải
Ta có: a2=a.a . Dựa vào đây ta tính được bình phương của 1 số.
Hướng dẫn giải
Câu a: Ta lập được bảng bình phương các số tự nhiên từ 0 đến 20 như sau
Câu b: Từ bảng ở câu a ta có
64 = 82; 169 = 132 ; 196 = 142
4. Giải bài 59 trang 28 SGK Toán 6 tập 1
a) Lập bảng lập phương của các số tự nhiên từ 0 đến 10.
b) Viết mỗi số sau thành lập phương của một số tự nhiên: 27; 125; 216
Phương pháp giải
Ta có: a3=a.a.a . Dựa vào đây ta tính được lập phương của 1 số.
Hướng dẫn giải
Câu a: Bảng lập phương các số tự nhiên từ 0 đến 10
Câu b
Cách 1
Theo bảng trên ta có: 27 = 33; 125 = 53; 216 = 63.
Cách 2
27=3.3.3=33
125 = 5.5.5 = 53;
216 = 6.6.6 = 63.
5. Giải bài 60 trang 28 SGK Toán 6 tập 1
Viết kết quả mỗi phép tính sau dưới dạng một lũy thừa.
a) 33 . 34; b) 52 . 57; c) 75 . 7.
Phương pháp giải
Áp dụng quy tắc nhân hai lũy thừa cùng cơ số:
am . an = am + n
Hướng dẫn giải
a) 33 . 34 = 33+4 = 37
b) 52 . 57 = 52+ 7 = 59
c) 75 . 7 =75+1 = 76
6. Giải bài 61 trang 28 SGK Toán 6 tập 1
Trong các số sau, số nào là lũy thừa của một số tự nhiên với số mũ lớn hơn 1 (chú ý rằng có những số có nhiều cách viết dưới dạng lũy thừa):
8,16,20,27,60,64,81,90,100?
Phương pháp giải
Một số viết được dưới dạng lũy thừa của một số tự nhiên với số mũ lớn hơn 1 nếu số đó viết được dưới dạng: an với n>1
Hướng dẫn giải
Các số viết được dưới dạng lũy thừa của một số tự nhiên với số mũ lớn hơn 1 là:
8=2.2.2=23
16=4.4=42 hoặc 16=2.2.2.2=24
27=3.3.3=33
64=8.8=82 hoặc 64=2.2.2.2.2.2=26 hoặc 64=4.4.4=43
81=9.9=92 hoặc 81=3.3.3.3=34;
100=10.10=102
Số 20,60,90 không viết được dưới dạng lũy thừa của một số tự nhiên.
7. Giải bài 62 trang 28 SGK Toán 6 tập 1
a) Tính: 102;103;104;105;106
b) Viết mỗi số sau dưới dạng lũy thừa của 10
1000; 1000000;
1 tỉ; 100...0 (12 chữ số 0)
Phương pháp giải
Áp dụng công thức: an=a.a.....a⏟n thừa số(n≠0)
Hướng dẫn giải
Câu a: Ta có
102=10.10=100;
103=10.10.10=1000;
104=10.10.10.10=10000;
105=10.10.10.10.10=100000;
106=10.10.10.10.10.10=1000000;
Câu b: Sử dụng lưu ý
10n=100.....0⏟nchữ số0
Nên ta có
1000=103
1000000=106
1 tỉ =1000000000=109
100.....0⏟12chữ số0=1012
8. Giải bài 63 trang 28 SGK Toán 6 tập 1
Điền dấu "x" vào ô thích hợp:
|
Câu |
Đúng |
Sai |
|
a) 23 . 22 = 26 |
|
|
|
b) =23 . 22 = 25 |
|
|
|
c) =54 . 5 = 54 |
|
|
Phương pháp giải
Áp dụng công thức nhân hai lũy thừa cùng cơ số: am.an=am+n
Hướng dẫn giải
Câu a: 23.22=23+2=25 nên dòng a) sai và dòng b) đúng.
Câu b: 54.5=54+1=55 nên dòng c) sai.
Ta có bảng sau
|
Câu |
Đúng |
Sai |
|
a) 23 . 22 = 26 |
|
X |
|
b) 23 . 22 = 25 |
X |
|
|
c) 54 . 5 = 54 |
|
X |
9. Giải bài 64 trang 29 SGK Toán 6 tập 1
Viết kết quả phép tính dưới dạng một lũy thừa:
a) 23.22.24
b) 102.103.105
c) x.x5
d) a3.a2.a5
Phương pháp giải
Áp dụng quy tắc: am.an=am+n và quy ước a1=a
Hướng dẫn giải
Câu a: 23.22.24=23+2+4=29;
Câu b: 102.103.105=102+3+5=1010
Câu c: x.x5=x1.x5=x1+5=x6
Câu d: a3.a2.a5=a3+2+5=a10
10. Giải bài 65 trang 29 SGK Toán 6 tập 1
Bằng cách tính, em hãy cho biết số nào lớn hơn trong hai số sau ?
a) 23 và 32
b) 24 và 42
c) ({2^5}\) và 52
d) 210 và 100.
Phương pháp giải
Áp dụng công thức: an=a.a...a⏟n thừa số a(n≠0) sau đó tính được kết quả từng lũy thừa rồi so sánh chúng với nhau.
Hướng dẫn giải
Câu a: Vì 23=2.2.2=8
32=3.3=9
Có 8<9 nên 23<32
Câu b: Vì 24=2.2.2.2=16
42=4.4=16
Có 16=16 nên 24=42
Câu c: Vì 25=2.2.2.2.2=32
52=5.5=25
Có: 32>25 nên 25>52
Câu d: Vì 210=2.2.2.2.2.2.2.2.2.2=1024>100
nên 210>100.
11. Giải bài 66 trang 29 SGK Toán 6 tập 1
Ta biết 112 = 121; 1112 = 12321.
Hãy dự đoán: 11112 bằng bao nhiêu? Kiểm tra lại dự đoán đó
Phương pháp giải
Sử dụng dữ kiện đề bài để dự đoán kết quả
Kiểm tra lại bằng cách sử dụng tính chất phân phối của phép nhân với phép cộng.
Hướng dẫn giải
Ta có 112=121;1112=12321 nên ta dự đoán 11112=1234321.
Thật vậy,
11112=1111.1111=1111.(1000+100+10+1)
=1111.1000+1111.100+1111.10+1111
=1111000+111100+11110+11
=1234321.
Tương tự ta có thể kết luận
111112=123454321;
1111112=12345654321;
11111112=1234567654321.
Tham khảo thêm
- doc Giải bài tập SGK Toán 6 Bài 1: Tập hợp và phần tử của tập hợp
- doc Giải bài tập SGK Toán 6 Bài 2: Tập hợp các số tự nhiên
- doc Giải bài tập SGK Toán 6 Bài 3: Ghi số tự nhiên
- doc Giải bài tập SGK Toán 6 Bài 4: Số phần tử của một tập hợp và tập hợp con
- doc Giải bài tập SGK Toán 6 Bài 5: Phép cộng và phép nhân
- doc Giải bài tập SGK Toán 6 Bài 6: Phép trừ và phép chia
- doc Giải bài tập SGK Toán 6 Bài 8: Chia hai lũy thừa cùng cơ số
- doc Giải bài tập SGK Toán 6 Bài 9: Thứ tự thực hiện các phép tính
- doc Giải bài tập SGK Toán 6 Bài 10: Tính chất chia hết của một tổng
- doc Giải bài tập SGK Toán 6 Bài 11: Dấu hiệu chia hết cho 2, cho 5
- doc Giải bài tập SGK Toán 6 Bài 12: Dấu hiệu chia hết cho 3, cho 9
- doc Giải bài tập SGK Toán 6 Bài 13: Ước và bội
- doc Giải bài tập SGK Toán 6 Bài 14: Số nguyên tố, hợp số và bảng số nguyên tố
- doc Giải bài tập SGK Toán 6 Bài 15: Phân tích một số ra thừa số nguyên tố
- doc Giải bài tập SGK Toán 6 Bài 16: Ước chung và bội chung
- doc Giải bài tập SGK Toán 6 Bài 17: Ước chung lớn nhất
- doc Giải bài tập SGK Toán 6 Bài 18: Bội chung nhỏ nhất