Giải bài tập SGK Toán 7 Bài 5: Vẽ góc cho biết số đo
Phần hướng dẫn giải bài tập SGK Vẽ góc cho biết số đo sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các dạng bài tập từ SGK Toán 6 Tập hai.
Mục lục nội dung

1. Giải bài 24 trang 84 SGK Toán 6 tập 2
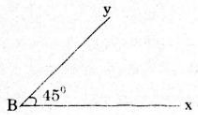
Vẽ góc \(xBy\) có số đo bằng \(45^0\)
Hướng dẫn : Vẽ tia \(Bx,\) sau đó trên một nửa mặt bẳng có bờ chứa tia \(Bx\) vẽ tia \(By\) sao cho \(\widehat {xBy} = {45^0}\)
Phương pháp giải
Xem lại cách vẽ hình ở phần ví dụ 1 SGK toán 6 tập 2 trang 83
Hướng dẫn giải
- Cách vẽ:
- Vẽ tia \(Bx;\)
- Đặt thước đo góc sao cho tâm của thước trùng với gốc \(B\) của tia \(Bx\) và tia \(Bx\) đi qua vạch \(0^0\)
- Vẽ tia \(By\) đi qua vạch \(45^0\) của thước. Ta vẽ được góc \(xBy = 45^0\)
2. Giải bài 25 trang 84 SGK Toán 6 tập 2
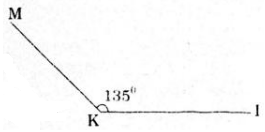
Vẽ góc \(IKM\) có số đo bằng \(135^0\)
Phương pháp giải
Vẽ tia \(KI,\) sau đó trên một nửa mặt bẳng có bờ chứa tia \(KI\) vẽ tia \(KM\) sao cho \(\widehat {IKM} = {135^0}\)
Hướng dẫn giải
- Cách vẽ:
- Vẽ tia \(KI.\)
- Đặt thước đo góc sao cho tâm của thước trùng với gốc \(K\) của tia \(KI\) và tia \(KI\) đi qua vạch \(0^0\)
- Vẽ tia \(KM\) đi qua vạch \(135\) của thước. Ta vẽ được góc \(IKM = 135^0\)
3. Giải bài 26 trang 84 SGK Toán 6 tập 2
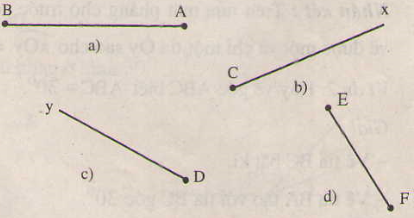
Vẽ góc cho biết một cạnh và số đo góc đó trong bốn trường hợp sau (h.35)
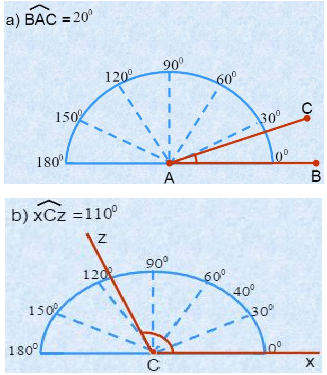
a) \(\widehat{BAC}=20^0\)
b) \(\widehat{ xCz}=110^0\)
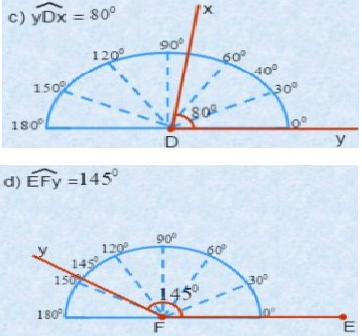
c) \(\widehat{ yDx}=80^0\)
d) \(\widehat{ EFy}=145^0\)
Phương pháp giải
Xem lại cách vẽ hình ở phần ví dụ 1 SGK toán 6 tập 2 trang 83
Hướng dẫn giải
Có thể vẽ hình như sau:
4. Giải bài 27 trang 85 SGK Toán 6 tập 2
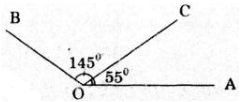
Trên cùng một mặt phẳng bờ chứa tia OA, vẽ hai tia OB, OC sao cho \(\widehat{BOA}=145^0,\) \(\widehat{COA}=55^0\)
Tính số đo góc \(BOC.\)
Phương pháp giải
- Trên cùng một nửa mặt phẳng bờ là đường thẳng chứa tia Ox, nếu có \(\widehat {xOy} < \widehat {xOz}<180^0\) thì tia Oy nằm giữa tia Ox và tia Oz.
- Nếu Oy nằm giữa hai tia Ox và Oz thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).
Hướng dẫn giải
Hai tia \(OB, OC\) cùng thuộc nửa mặt phẳng bờ chứa tia \(OA\) mà
\(\widehat{COA}<\widehat{BOA}\) (vì \(55^0<145^0)\) nên tia \(OC\) nằm giữa hai tia \(OA,OB\)
suy ra \(\widehat{COA}+\widehat{COB}=\widehat{BOA}\)
hay \(55^0+\widehat{COB}=145^0\)
Vậy \(\widehat{COB}=145^0-55^0=90^0\)
5. Giải bài 28 trang 85 SGK Toán 6 tập 2
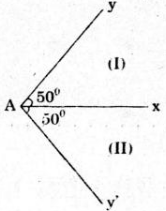
Trên mặt phẳng, cho tia Ax. Có thể vẽ được mấy tia Ay sao cho \(\widehat{xAy}=50^0\)
Phương pháp giải
Xem lại cách vẽ hình ở phần ví dụ 1 SGK toán 6 tập 2 trang 83
Hướng dẫn giải
Vì \(Ax\) là bờ chung của hai nửa mặt phẳng đối nhau (nửa mặt phẳng (I) và (II))
Trên mỗi nửa mặt phẳng ta vẽ được một tia \(Ay\) sao cho \(\widehat{xAy}=50^0\)
Do đó ta vẽ được hai tia \(Ay\) thỏa mãn yêu cầu của đề bài
Hình vẽ:
6. Giải bài 29 trang 85 SGK Toán 6 tập 2
Gọi \(Ot, Ot'\) là hai tia nằm trên cùng một nửa mặt phẳng bờ là đường thẳng \(xy\) đi qua \(O.\) Biết \(\widehat{xOt}=30^0,\) \(\widehat{yOt'}=60^0.\) Tính số đo các góc \(yOt, tOt'.\)
Phương pháp giải
Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\) thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\).
Trên nửa mặt phẳng bờ chứa tia \(Ox\) có hai tia \(Oy, Oz\) mà \(\widehat{xOy}< \widehat{xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox, Oz.\)
Hai góc kề bù thì có tổng số đo bằng 180 độ.
Hướng dẫn giải
Vì \(Ox\) và \(Oy\) là hai tia đối nhau nên \(\widehat{xOy}=180^0\) (góc bẹt)
Ta có \(Ot\) nằm trên nửa mặt phẳng có bờ là đường thẳng \(xy\), \(\widehat{xOt}=30^0\)
Vì \(\widehat{xOt}<\widehat{xOy}\) (vì \(30^0<180^0)\) nên tia \(Ot\) nằm giữa hai tia \(Ox\) và \(Oy\)
Suy ra \(\widehat{xOt}+\widehat{yOt}=\widehat{xOy}\)
Do đó \(\widehat{yOt}=\widehat{xOy}-\widehat{xOt}\) \(= 180^0-30^0=150^0 \)
Hai tia \(Ot'\) và \(Ot\) cùng thuộc nửa mặt phẳng bờ \(Oy\) mà \(\widehat{yOt'}<\widehat{yOt}\) (vì \(60^0<150^0)\) nên tia \(Ot'\) nằm giữa hai tia \(Oy\) và \(Ot.\)
Suy ra \(\widehat{yOt'}+\widehat{t'Ot}=\widehat{tOy}\)
Thay số ta được: \(60^0+\widehat{t'Ot}=150^0\)
Suy ra: \(\widehat{t'Ot}=150^0-60^0=90^0\)
Tham khảo thêm
- doc Giải bài tập SGK Toán 7 Bài 1: Nửa mặt phẳng
- doc Giải bài tập SGK Toán 7 Bài 2: Góc
- doc Giải bài tập SGK Toán 7 Bài 2: Số đo góc
- doc Giải bài tập SGK Toán 7 Bài 4: Khi nào góc xOy + góc yOz= góc xOz?
- doc Giải bài tập SGK Toán 7 Bài 6: Tia phân giác của góc
- doc Giải bài tập SGK Toán 6 Bài 8: Đường tròn
- doc Giải bài tập SGK Toán 6 Bài 9: Tam giác
- doc Giải bài tập SGK Toán 6 Ôn tập phần Hình học