Giải bài tập SGK Toán 8 Bài 4: Những hằng đẳng thức đáng nhớ (tiếp theo)
Phần hướng dẫn giải bài tập Những hằng đẳng thức đáng nhớ (tiếp) sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Đại số 8 Tập 1
Mục lục nội dung

1. Giải bài 26 trang 14 SGK Toán 8 tập 1
Tính
a) \((2x^2 + 3y)^3\)
b) \(\left(\dfrac{1}{3}x -3\right)^3\)
Phương pháp giải
Áp dụng
- \({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)
- \({\left( {A.B} \right)^n} = {A^n}.{B^n}\)
Hướng dẫn giải
Câu a
\(\eqalign{
& {(2{x^2} + {\rm{ }}3y)^3} = {(2{x^2})^3} + 3.{(2{x^2})^2}.3y + 3.{\rm{ }}2{x^2}.{\left( {3y} \right)^2} + {\left( {3y} \right)^3} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 8{x^6} + 3.4{x^4}.3y + 3.2{x^2}.9{y^2} + 27{y^3} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,= 8{x^6} + 36{x^4}y + 54{x^2}{y^2} + 27{y^3} \cr} \)
Câu b
\(\eqalign{
& {\left( {{1 \over 2}x - 3} \right)^3} = {\left( {{1 \over 2}x} \right)^3} - 3.{\left( {{1 \over 2}x} \right)^2}.3 + 3.\left( {{1 \over 2}x} \right){.3^2} - {3^3} \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;\;\;\;\;\;= {1 \over 8}{x^3} - 3.{1 \over 4}{x^2}.3 + 3.{1 \over 2}x.9 - 27 \cr
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\;\;\;\;\;\; = {1 \over 8}{x^3} - {9 \over 4}{x^2} + {{27} \over 2}x - 27 \cr} \)
2. Giải bài 27 trang 14 SGK Toán 8 tập 1
Viết các biểu thức sau dưới dạng lập phương của một tổng hoặc một hiệu:
a) \(-x^3 + 3x^2 -3x + 1\)
b) \(8 - 12x + 6x^2 - x^3\)
Phương pháp giải
Áp dụng: Hằng đẳng thức lập phương của một hiệu.
\({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Hướng dẫn giải
Câu a
\(\eqalign{
& \,\, - {x^3} + 3{x^2} - 3x + 1 \cr
& = 1 - 3x + 3{x^2} - {x^3} \cr
& = {1^3} - {3.1^2}.x + 3.1.{x^2} - {x^3} \cr
& = {\left( {1 - x} \right)^3} \cr} \)
Câu b
\(\eqalign{
& \,\,8 - 12x + 6{x^2} - {x^3} \cr
& = {2^3} - {3.2^2}.x + 3.2.{x^2} - {x^3} \cr
& = {\left( {2 - x} \right)^3} \cr} \)
3. Giải bài 28 trang 14 SGK Toán 8 tập 1
Tính giá trị của biểu thức:
a) \( x^3 + 12x^2 + 48x + 64\) tại \(x = 6\)
b) \(x^3 - 6x^2 + 12x - 8\) tại \(x = 22\)
Phương pháp giải
- Bước 1: Ta đưa hai biểu thức đã cho về dạng lập phương của một tổng, lập phương của một hiệu.
- Bước 2: Thay giá trị của \(x\) để tính giá trị của biểu thức.
Hướng dẫn giải
Câu a
\(\,{x^3} + 12{x^2} + 48{\rm{x}} + 64 \)\(= {{\rm{x}}^3} + 3.{{\rm{x}}^2}.4 + 3.x{.4^2} + {4^3} = {\left( {x + 4} \right)^3}\)
Với \(x = 6\) ta có: \({\left( {6 + 4} \right)^3} = {10^3} = 1000.\)
Câu b
\(\,{x^3} - 6{{\rm{x}}^2} + 12{\rm{x}} - 8 \)\(= {x^3} - 3.{{\rm{x}}^2}.2 + 3.x{.2^2} - {2^3} = {\left( {x - 2} \right)^3}\)
Với \(x = 22\) ta có: \({\left( {22 - 2} \right)^3} = {20^3} = 8000.\)
4. Giải bài 29 trang 14 SGK Toán 8 tập 1
Đố: Đức tính đáng quý
Hãy viết mỗi biểu thức sau dưới dạng bình phương hoặc lập phương của một tổng hoặc một hiệu, rồi điền chữ cùng dòng với biểu thức đó vào bảng cho thích hợp. Sau khi thêm dấu, em sẽ tìm ra một trong những đức tính quý báu của con người.
\({x^3} - 3{x^2} + 3x - 1\) \(N\)
\(16 + 8x + {x^2}\) \( U\)
\(3{x^2} + 3x + 1 + {x^3}\) \(H\)
\(1 - 2y + {y^2}\) \(Â\)
.jpg)
Phương pháp giải
Áp dụng: Hằng đẳng thức lập phương của một tổng, lập phương của một hiệu, bình phương của một tổng hoặc một hiệu.
- \((A+B)^2=A^2+2AB+B^2\)
- \((A-B)^2=A^2-2AB+B^2\)
- \({\left( {A + B} \right)^3} = {A^3} + 3{A^2}B + 3A{B^2} + {B^3}\)
- \({\left( {A - B} \right)^3} = {A^3} - 3{A^2}B + 3A{B^2} - {B^3}\)
Hướng dẫn giải
Ta có
N: \({x^3} - 3{x^2} + 3x - 1 \)
\(= {x^{3}} - 3.{x^2}.1 + 3.x{.1^2} - {1^3} = {\left( {x - 1} \right)^3}\)
U: \(16 + 8x + {x^2} = {4^2} + 2.4.x + {x^2} \) \(= {\left( {4 + x} \right)^2} = {\left( {x + 4} \right)^2}\) H: \(3{x^2} + 3x + 1 + {x^3} \)
\(= {x^3} + 3{x^2} + 3x + 1 \)
\(= {x^3} + 3.{x^2}.1 + 3.x{.1^2} + {1^3} \)
\(= {\left( {x + 1} \right)^3} = {\left( {1 + x} \right)^3}\)
Â: \(1 - 2y + {y^2} = {y^2} - 2y + 1 \)
\(= {y^2} - 2.y.1 + {1^2} \)
\(= {\left( {y - 1} \right)^2} = {\left( {1 - y} \right)^2}\)
Ta điền vào bảng như sau:
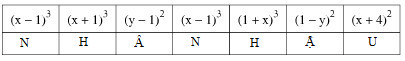
Vậy: Đức tính đáng quý là "NHÂN HẬU"
Tham khảo thêm
- doc Giải bài tập SGK Toán 8 Bài 1: Nhân đơn thức với đa thức
- doc Giải bài tập SGK Toán 8 Bài 2: Nhân đa thức với đa thức
- doc Giải bài tập SGK Toán 8 Bài 3: Những hằng đẳng thức đáng nhớ
- doc Giải bài tập SGK Toán 8 Bài 5: Những hằng đẳng thức đáng nhớ (tiếp theo)
- doc Giải bài tập SGK Toán 8 Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
- doc Giải bài tập SGK Toán 8 Bài 7: Phân tích đa thức thành nhân tử bằng phương pháp dùng hằng đẳng thức
- doc Giải bài tập SGK Toán 8 Bài 8: Phân tích đa thức thành nhân tử bằng phương pháp nhóm hạng tử
- doc Giải bài tập SGK Toán 8 Bài 9: Phân tích đa thức thành nhân tử bằng cách phối hợp nhiều phương pháp
- doc Giải bài tập SGK Toán 8 Bài 10: Chia đơn thức cho đơn thức
- doc Giải bài tập SGK Toán 8 Bài 11: Chia đa thức cho đơn thức
- doc Giải bài tập SGK Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp
