Giải bài tập SGK Toán 8 Bài 4: Khái niệm hai tam giác đồng dạng

Trong hai mệnh đề sau, mệnh đề nào đúng? Mệnh đề nào sai?

a) Hai tam giác bằng nhau thì đồng dạng với nhau.

b) Hai tam giác đồng dạng với nhau thì bằng nhau.

Phương pháp giải

Áp dụng định nghĩa hai tam giác đồng dạng.

Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu:

\(\widehat{A'} =  \widehat{A}\); \(\widehat{B'} = \widehat{B}\); \(\widehat{C'}= \widehat{C}\).

\(\dfrac{A'B'}{AB}  = \dfrac{B'C'}{BC} =  \dfrac{C'A'}{CA}\)

Hướng dẫn giải

a) a là mệnh đề đúng. Bởi vì khi hai tam giác bằng nhau thì các góc tương ứng của hai tam giác này bằng nhau và tỉ lệ các cạnh tương ứng của chúng đều bằng nhau và bằng 1 nên theo định nghĩa hai tam giác đồng dạng thì hai tam giác bằng nhau sẽ đồng dạng với nhau.

b) b là mệnh đề sai. Bởi vì nếu tỉ số đồng dạng \(k ≠ 1\) thì các cạnh của chúng sẽ có độ dài khác nhau. Do đó hai tam giác sẽ không bằng nhau.

\(∆A'B'C'\) ∽ \(∆A"B"C"\) theo tỉ số đồng dạng \(k_1\), \(∆A"B"C"\) ∽ \(∆ ABC\) theo tỉ số đồng dạng \(k_2\). Hỏi tam giác \(A’B’C’\) đồng dạng với tam giác \(ABC\) theo tỉ số nào?

Phương pháp giải

Áp dụng tính chất: Nếu \(∆A'B'C'\) ∽  \(∆A"B"C"\) và \(∆A"B"C"\) ∽  \(∆ABC\) thì \(∆A'B'C'\) ∽ \(∆ABC.\)

Hướng dẫn giải

\( ∆A'B'C'\) ∽ \(∆A"B"C"\) theo tỉ số đồng dạng \(k_1=\dfrac{A'B'}{A"B"}\)

 \(∆A"B"C"\) ∽ \(∆ ABC\) theo tỉ số đồng dạng \(k_2=\dfrac{A"B"}{AB}\)

Theo tính chất 3 của hai tam giác đồng dạng thì \(∆A'B'C'\) ∽ \(∆ABC.\)

Tỉ số đồng dạng \(k= \dfrac{A'B'}{AB} = \dfrac{A'B'.A"B"}{A''B''.AB} \)\(\,= \dfrac{A'B'}{A"B"}.\dfrac{A"B"}{AB}\)

Vậy \(k = k_1.k_2\).

Cho tam giác \(ABC\). Hãy vẽ một tam giác đồng dạng với tam giác \(ABC\) theo tỉ số \(\dfrac{1}{2}\).

Phương pháp giải

Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

Hướng dẫn giải

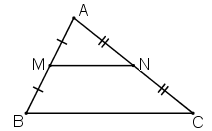
Lấy trung điểm \(M\) của \(AB\), \(N\) là trung điểm của \(AC\)

Khi đó tam giác \(AMN\) là tam giác cần dựng.

Thật vậy:

Vì \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AC\)

\( \Rightarrow \) \(MN\) là đường trung bình của tam giác \(ABC\) (dấu hiệu nhận biết đường trung bình của tam giác)

\( \Rightarrow \) \(MN // BC\) (tính chất đường trung bình của tam giác)

\(\Rightarrow \) \(∆ AMN\) ∽  \(∆ABC\) theo tỉ số \(k = \dfrac{1}{2}\) (Theo định lí trang 71 SGK Toán 8 Tập 2).

Cho tam giác \(ABC\) vẽ tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\) theo tỉ số đồng dạng là \(k = \dfrac{2}{3}\)

Phương pháp giải

Áp dụng định lí: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

Hướng dẫn giải

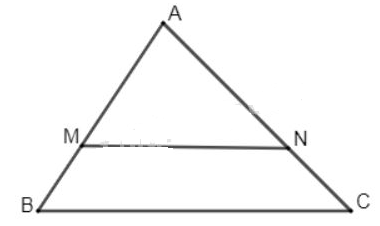
Trên cạnh \(AB\) lấy điểm \(M\) sao cho \(AM= \dfrac{2}{3}AB.\)

Từ \(M\) kẻ đường song song với \(BC\) cắt \(AC\) tại \(N\).

Ta có \(∆AMN\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k=\dfrac{AM}{AB}=\dfrac{2}{3}\) 

*) Dựng  \(∆A'B'C' = ∆AMN\) (theo trường hợp cạnh cạnh cạnh) 

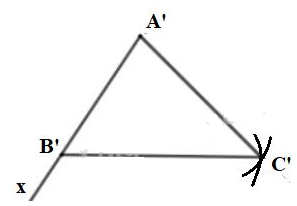
- Dựng tia \(A’x\), trên tia \(A’x\) lấy \(B’\) sao cho \(A’B’ = AM\)

- Dựng cung tròn tâm \(A’\) bán kính \(AN\) và cung tròn tâm \(B’\) bán kính \(MN\), hai cung tròn cắt nhau tại \(C’\)

- Nối \(A'C', B'C'\) ta được tam giác \(A'B'C'\) phải dựng.

Mà \(∆AMN\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k=\dfrac{2}{3}\) nên \(∆A'B'C'\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k=\dfrac{2}{3}\).

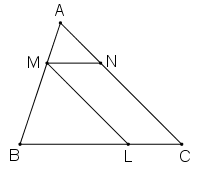
Từ \(M\) thuộc cạnh \(AB\) của tam giác \(ABC\) với \(AM = \dfrac{1}{2}MB\). Kẻ các tia song song với \(AC\) và \( BC\), chúng cắt \(BC\) và \(AC\) lần lượt tại \(L\) và \(N.\)

a) Nêu tất cả các cặp tam giác đồng dạng.

b) Đối với mỗi cặp tam giác đồng dạng, hãy viết các cặp góc bằng nhau và tỉ số đồng dạng tương ứng.

Phương pháp giải

Áp dụng:

- Hệ quả: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.

- Tính chất hai tam giác đồng dạng.

Hướng dẫn giải

a) Áp dụng: Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho, ta có:

\(MN // BC\)  (gt) \( \Rightarrow \) \(∆AMN\) ∽ \(∆ABC\) 

\(ML // AC\) (gt) \( \Rightarrow \) \(∆MBL\) ∽ \(∆ABC\).

và \(∆AMN\) ∽ \(∆MBL\) (vì cùng đồng dạng với tam giác \(ABC\)) 

b) \(∆AMN\) ∽ \(∆ABC\) có:

\(\widehat{AMN}\) = \(\widehat{ABC}\); \(\widehat{ANM}\) = \(\widehat{ACB}\); \(\widehat{A}\) chung

Tỉ số đồng dạng \(k_1=\dfrac{AM}{AB}= \dfrac{1}{3}\) (vì \(AM=\dfrac{1}{2}MB\))

 \(∆MBL\) ∽ \(∆ABC\) có: 

\(\widehat{BML} = \widehat{BAC}\), \(\widehat{B}\) chung, \(\widehat{MLB} = \widehat{ACB}\)

Tỉ số đồng dạng \(k_2=\dfrac{MB}{AB}= \dfrac{2}{3}\)

\(∆AMN\) ∽ \(∆MBL\) có:

\(\widehat{MAN} = \widehat{BML}\), \(\widehat{AMN} = \widehat{MBL}\), \(\widehat{ANM} = \widehat{MLB}\)

Tỉ số đồng dạng \(k_3=\dfrac{AM}{MB} = \dfrac{1}{2}\) 

\(∆A'B'C'\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k= \dfrac{3}{5}\).

a) Tính tỉ số chu vi của hai tam giác đã cho.

b) Cho biết hiệu chu vi của hai tam giác trên là \(40\) dm, tính chu vi của mỗi tam giác.

Phương pháp giải

Hai tam giác \(A'B'C'\) và \(ABC\) đồng dạng có một số tính chất:

- \(∆ABC \) đồng dạng \( ∆A'B'C'\)

- Nếu \(∆A'B'C'\) đồng dạng \( ∆ABC\) thì \( ∆ABC\) đồng dạng \(∆A'B'C'\)

- Nếu \(∆A'B'C'\) đồng dạng \( ∆A"B"C" \) và \(∆A"B"C"\) đồng dạng \( ∆ABC\) thì \(∆A'B'C' \) đồng dạng \( ∆ABC\).

Hướng dẫn giải

a) Vì \(\dfrac{C_{A'B'C'}}{C_{ABC}}= \dfrac{3}{5}\) suy ra \( \dfrac{C_{ABC}}{5}= \dfrac{C_{A'B'C'}}{3} \) mà \(C_{ABC}- C_{A'B'C'} = 40\,dm\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\( \dfrac{C_{ABC}}{5}= \dfrac{C_{A'B'C'}}{3} \)\(\,=\dfrac{{{C_{ABC}} - {C_{A'B'C'}}}}{{5 - 3}}\)\(\,= \dfrac{40}{2}= 20\)

\( \Rightarrow C_{ABC}= 5.20=100\, dm\)

\(C_{A'B'C'}= 20.3=60\, dm\) 

\(∆A'B'C'\) ∽ \(∆ABC\) theo tỉ số đồng dạng \(k= \dfrac{3}{5}\) (gt)

\( \Rightarrow \dfrac{A'B'}{AB} = \dfrac{B'C'}{BC} = \dfrac{C'A'}{CA} = \dfrac{3}{5}\) (tính chất hai tam giác đồng dạng)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\dfrac{{A'B'}}{{AB}} = \dfrac{{B'C'}}{{BC}} = \dfrac{{C'A'}}{{CA}}\)\(\,= \dfrac{A'B'+B'C'+C'A'}{AB+BC+CA}\)\(\,= \dfrac{C_{A'B'C'}}{C_{ABC}}= \dfrac{3}{5}\)

Với \(C_{A'B'C'};C_{ABC}\) lần lượt là chu vi hai tam giác \(A'B'C';ABC\) 

Vậy tỉ số chu vi của \(∆A'B'C'\) và \(∆ABC\) là \(\dfrac{3}{5}\).

b) Vì \(\dfrac{C_{A'B'C'}}{C_{ABC}}= \dfrac{3}{5}\) suy ra \( \dfrac{C_{ABC}}{5}= \dfrac{C_{A'B'C'}}{3} \) mà \(C_{ABC}- C_{A'B'C'} = 40\,dm\)

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\( \dfrac{C_{ABC}}{5}= \dfrac{C_{A'B'C'}}{3} \)\(\,=\dfrac{{{C_{ABC}} - {C_{A'B'C'}}}}{{5 - 3}}\)\(\,= \dfrac{40}{2}= 20\)

\( \Rightarrow C_{ABC}= 5.20=100\, dm\)

\(C_{A'B'C'}= 20.3=60\, dm\)