Giải bài tập SGK Toán 8 Bài 1: Đa giác - Đa giác đều

Hãy vẽ phác một lục giác lồi. Hãy nêu cách nhận biết một đa giác lồi.

Phương pháp giải

Áp dụng định nghĩa đa giác lồi.

Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa bất kì cạnh nào của đa giác đó.

Hướng dẫn giải

Vẽ phác một lục giác lồi.

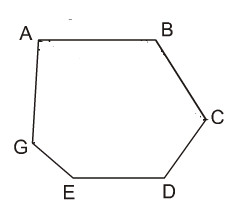
Cách nhận biết một đa giác lồi: Một đa giác lồi là một đa giác thỏa mãn 2 điều kiện sau:

- Các cạnh chỉ cắt nhau tại các đỉnh, nghĩa là không có hai cạnh nào cắt nhau tại một điểm mà không phải là đỉnh. Một đa giác thỏa mãn điều kiện này là đa giác đơn.

- Đa giác luôn nằm trong một nửa mặt phẳng mà bờ là đường thẳng chứa một cạnh tùy ý của nó. Một đa giác đơn thỏa mãn thêm điều kiện này là đa giác lồi

Cho ví dụ về đa giác không đều trong mỗi trường hợp sau:

a) Có tất cả các cạnh bằng nhau;

b) Có tất cả các góc bằng nhau.

Phương pháp giải

Áp dụng định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và tất cả các góc bằng nhau.

Hướng dẫn giải

Câu a

Hình thoi có tất cả các cạnh bằng nhau nhưng các góc có thể không bằng nhau nên hình thoi không buộc phải là đa giác đều.

Câu b

Hình chữ nhật có tất cả các góc bằng nhau nhưng các cạnh có thể không bằng nhau nên hình chữ nhật không buộc phải là đa giác đều.

Cho hình thoi ABCD có \(\widehat{A}=60^0\) . Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Chứng minh rằng đa giác EBFGDH là lục giác đều.

Phương pháp giải

Áp dụng:

- Hình thoi có tất cả các cạnh bằng nhau,

- Lục giác đều là hình có sáu cạnh bằng nhau và sáu góc bằng nhau.

Hướng dẫn giải

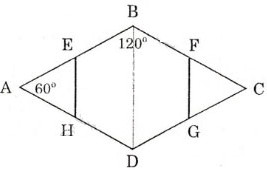
Vì \(ABCD\) là hình thoi (giả thiết) và \(\widehat A = {60^0}\) (giả thiết)

Do đó \(AB = BC = CD = DA\); \(AB//DC;\,BC//AD\).

Lại có \(E,F,G,H\) lần lượt là trung điểm của \(AB,BC,CD,DA\) nên \(AE = EB = BF = FC = CG = GD\)\(\, = DH = HA\)

Vì \(AD//BC\) nên \(\widehat A + \widehat {ABC} = {180^0}\) (\(2\) góc trong cùng phía bù nhau)

\( \Rightarrow \widehat {ABC} = {180^0} - \widehat A = {180^0} - {60^0} \)\(= {120^0}\)

\( \Rightarrow \widehat {ABC} = \widehat {ADC} = {120^0}\) (tính chất hình thoi)

\(\Delta EAH\) có \(AE=AH\) (chứng minh trên) và \(\widehat A=60^0\) nên là tam giác đều (vì tam giác cân có một góc \(60^0\) là tam giác đều)

\( \Rightarrow \widehat {AEH} = \widehat {AHE} = {60^0}\) và \(AE=EH=AH\) (tính chất tam giác đều) 

\(\left\{ \begin{array}{l}
\widehat {AEH} + \widehat {HEB} = {180^0}\\
\widehat {AHE} + \widehat {EHD} = {180^0}
\end{array} \right.\)  (hai góc kề bù)

\( \Rightarrow \widehat {HEB} = \widehat {EH{\rm{D}}} = {180^0} - {60^0} = {120^0}\)

Tương tự:

\(\Delta CFG\) có \(CF=CG\) (chứng minh trên) và \(\widehat C=\widehat A =60^0\) (do ABCD là hình thoi) nên là \(\Delta CFG\) tam giác đều (vì tam giác cân có một góc \(60^0\) là tam giác đều)

\( \Rightarrow \widehat {CFG} = \widehat {CGF} = {60^0}\) và \(CF=FG=CG\) (tính chất tam giác đều) 

\(\left\{ \begin{array}{l}
\widehat {CFG} + \widehat {BFG} = {180^0}\\
\widehat {CGF} + \widehat {FGD} = {180^0}
\end{array} \right.\)  (hai góc kề bù)

\( \Rightarrow \widehat {BFG} = \widehat {FGD} = {180^0} - {60^0} = {120^0}\)

Từ đó ta suy ra: \( EB = BF = GD=HD\)\(\, = EH= FG\) 

\(\widehat {ABC} = \widehat {ADC} \)\(=\widehat {HEB} = \widehat {EH{\rm{D}}}\)\(=\widehat {BFG} =\widehat{F GD} = {120^0}\)

Vậy đa giác \(EBFGDH\) có tất cả các góc bằng nhau, tất cả các cạnh bằng nhau ( bằng nửa cạnh hình thoi)

Nên \(EBFGDH\) là một lục giác đều (dấu hiệu nhận biết lục giác đều)

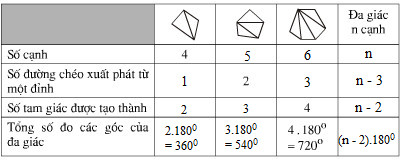
Điền số thích hợp vào các ô trống trong bảng

Phương pháp giải

Áp dụng các công thức sau: 

- Tổng số đo các góc của đa giác \(n\) cạnh là \(\left( {n - 2} \right){.180^o}\)

- Số đo một góc của đa giác đều \(n\) cạnh là \(\dfrac{{\left( {n - 2} \right){{.180}^0}}}{n}\).

- Số đường chéo của đa giác \(n\) cạnh là \(\dfrac{{n\left( {n - 3} \right)}}{2}\).

Hướng dẫn giải

 Dựa vào công thức ta tính được các giá trị trong bảng:

Tính số đo mỗi góc của ngũ giác đều, lục giác đều, \(n\) - giác đều.

Phương pháp giải

Áp dụng công thức:

+) Tổng số đo các góc của đa giác n cạnh: \((n-2).180^o\).

+) Số đo một góc của đa giác đều n cạnh: \(\dfrac{{\left( {n - 2} \right){{.180}^0}}}{n}\).

Hướng dẫn giải

Tổng số đo các góc của hình \(n\)- giác bằng \((n - 2).180^{\circ}\)

Suy ra số đo mỗi góc của hình \(n\)- giác đều là \(\dfrac{\left ( n-2 \right ).180^{\circ}}{n}\)

Áp dụng công thức trên, ta có:

- Số đo mỗi góc của ngũ giác đều là \(\dfrac{\left ( 5-2 \right ).180^{\circ}}{5}=108^0\)

- Số đo mỗi góc của lục giác đều là \(\dfrac{\left ( 6-2 \right ).180^{\circ}}{6} = 120^{\circ}\)