Giải bài tập SGK Toán 8 Bài 5: Diện tích hình thoi
Hướng dẫn giải bài tập SGK Hình học 8 Bài 5 Diện tích hình thoi sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 32 trang 128 SGK Toán 8 tập 1
a) Hãy vẽ một tứ giác có độ dài hai đường chéo là \(3,6cm; 6cm\) và hai đường chéo đó vuông góc với nhau. Có thể vẽ được bao nhiêu tứ giác như vậy? Hãy tính diện tích mỗi tứ giác vừa vẽ?
b) Hãy tính diện tích hình vuông có độ dài đường chéo là \(d\).
Phương pháp giải
Áp dụng cách tính diện tích của một tứ giác có hai đường chéo vuông góc:
- Diện tích của một tứ giác có hai đường chéo vuông góc bằng nửa tích độ dài hai đường chéo đó.
\({S_{ABCD}}=\dfrac{1}{2} AC. BD\)
Hướng dẫn giải
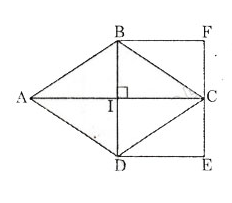
a) Học sinh tự vẽ tứ giác thỏa mãn điều kiện đề bài, chẳng hạn như tứ giác \(ABCD\) ở hình vẽ có:
\(AC = 6cm\)
\(BD = 3,6cm\)
\(AC \perp BD\)
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài.
Diện tích của tứ giác vừa vẽ là: \(S_{ABCD}= \dfrac{1}{2} AC. BD = \dfrac{1}{2}6. 3,6 = 10,8\) (\(cm^2\))
b) Diện tích hình vuông có độ dài đường chéo là \(d\)
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:
\(S = \dfrac{1}{2} d.d = \dfrac{1}{2} d^2\)
2. Giải bài 33 trang 128 SGK Toán 8 tập 1
Vẽ hình chữ nhật có một cạnh bằng đường chéo của một hình thoi cho trước và có diện tích bằng diện tích của hình thoi đó. Từ đó suy ra cách tính diện tích hình thoi.
Phương pháp giải
- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.
\(S=\dfrac{1}{2}{d_1}.{d_2}\)
- Diện tích hình chữ nhật bằng tích hai kích thước của nó
\( S = a.b\)
(\(S\) là diện tích, \(a\) là chiều dài, \(b\) là chiều rộng của hình chữ nhật).
Hướng dẫn giải
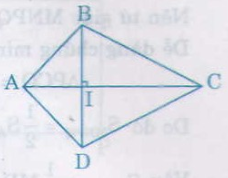
Cho hình thoi \(ABCD\) có hai đường chéo cắt nhau tại \(I\). Suy ra \(I\) là trung điểm \(AC\) hay \(IC=\dfrac{1}{2}\) \(AC\) (tính chất)
Vẽ hình chữ nhật có một cạnh là đường chéo \(BD\), cạnh kia bằng \(IC\) ( \(IC=\dfrac{1}{2}\) \(AC\))
Khi đó diện tích của hình chữ nhật \(BFED\) bằng diện tích hình thoi \(ABCD\).
Thật vậy:
\({S_{BF{\rm{ED}}}} = BD.IC = B{\rm{D}}.\dfrac{1}{2}AC \)\(= \dfrac{1}{2}B{\rm{D}}.AC = {S_{ABC{\rm{D}}}}.\)
Từ đó suy ra cách tính diện tích hình thoi: Diện tích hình thoi bằng nửa tích hai đường chéo.
3. Giải bài 34 trang 128 SGK Toán 8 tập 1
Cho một hình chữ nhật. Vẽ tứ giác có các đỉnh là trung điểm các cạnh của hình chữ nhật . Vì sao tứ giác này là một hình thoi? So sánh diện tích hình thoi và diện tích hình chữ nhật, từ đó suy ra cách tính diện tích hình thoi.
Phương pháp giải
- Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa độ dài cạnh ấy.
- Diện tích hình chữ nhật có kích thước hai cạnh \(a,b\) là \(S=a.b\).
- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.
\(S=\dfrac{1}{2}{d_1}.{d_2}\)
Hướng dẫn giải
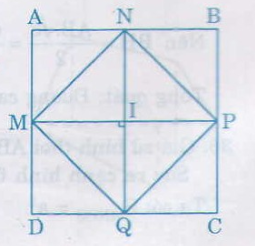
Ta có:
\(MN\) là đường trung bình của tam giác \(ABD\) nên \(MN = \dfrac{1}{2}BD\) (tính chất)
\(PQ\) là đường trung bình của tam giác \(CBD\) nên \(PQ = \dfrac{1}{2}BD\) (tính chất)
\(NP\) là đường trung bình của tam giác \(ABC\) nên \(NP = \dfrac{1}{2}AC\) (tính chất)
\(MQ\) là đường trung bình của tam giác \(ADC\) nên \(MQ = \dfrac{1}{2}AC\) (tính chất)
Mà \(AC = BD\) (tính chất hình chữ nhật) nên suy ra \(MN = PQ = NP = MQ.\)
Nên tứ giác \(MNPQ\) là hình thoi vì có bốn cạnh bằng nhau (dấu hiệu nhận biết hình thoi)
Ta có: \(∆AMN = ∆INM , ∆BPN = ∆NIP, \)\(\,∆PCQ = ∆IQP, ∆DMQ = ∆IQM\)
\( \Rightarrow {S_{AMN}} = {S_{INM}},{S_{BPN}} = {S_{NIP}},\)\({S_{PCQ}} = {S_{IQP}},{S_{DMQ}} = {S_{IQM}}\)
Ta có:
\({S_{MNPQ}} = {S_{MNI}} + {S_{NIP}} + {S_{IQP}} \)\(+ {S_{MQI}}\)
\(\begin{array}{l}
= {S_{AMN}} + {S_{BNP}} + {S_{PCQ}} + {S_{MQD}}\\
= \dfrac{1}{2}{S_{ABC{\rm{D}}}} = \dfrac{1}{2}.AB.AD \\= \dfrac{1}{2}.MP.NQ
\end{array}\)
Vậy \({S_{MNPQ}}=\dfrac{1}{2} MP.NQ\).
Do đó diện tích hình thoi bằng nửa tích hai đường chéo.
4. Giải bài 35 trang 129 SGK Toán 8 tập 1
Tính diện tích hình thoi có cạnh dài \(6\,cm\) và một trong các góc của nó có số đo là \(60^{\circ}\)
Phương pháp giải
- Tam giác đều là tam giác có ba cạnh bằng nhau.
- Định lí Pytago: Bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
- Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.
\(S = ah\)
- Diện tích hình thoi bằng nửa tích độ dài hai đường chéo.
\(S=\dfrac{1}{2}{d_1}.{d_2}\)
Hướng dẫn giải
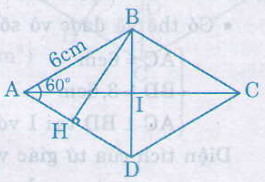
Xét hình thoi \(ABCD\) có cạnh \(6cm\) và \(\widehat {BAD}=60^0\). Kẻ \(BH\bot AD\)
Công thức tổng quát tính độ dài đường cao BH:
Ta có \(∆ABD\) là tam giác đều (vì tam giác \(ABD\) cân có \(\widehat{A}\) = \(60^{\circ}\) )
Tam giác \(ABD\) đều nên đường cao BH cũng là đường trung tuyến hay \(H\) là trung điểm của \(AD\)
Suy ra \(AH=\dfrac{AD}{2}=\dfrac{AB}{2}\)
Áp dụng định lí Pytago vào tam giác vuông \(ABH\) có:
\(B{H^2} = A{B^2} - A{H^2}\)
\( = A{B^2}-\left ( \dfrac{AB}{2} \right )^{2}\)
\( = A{B^2}-\dfrac{AB^{2}}{4} = \dfrac{3AB^{2}}{4}\).
\( \Rightarrow BH = \dfrac{AB.\sqrt{3}}2\) (cm)
Tổng quát: Đường cao tam giác đều cạnh \(a\) có độ dài là: \({h_a}=\dfrac{a\sqrt{3}}2\)
Áp dụng vào bài với cạnh \(a=6cm\) thì \( BH = \dfrac{a.\sqrt{3}}2 = \dfrac{6\sqrt{3}}2 = 3\sqrt3\) (cm)
Tính diện tích hình thoi ABCD.
Ta có: \( BH = 3\sqrt3\) (cm) (theo trên)
\({S_{ABCD}}= BH. AD = 3\sqrt 3. 6 \)\(\,= 18\sqrt 3\;(c{m^2})\)
5. Giải bài 36 trang 129 SGK Toán 8 tập 1
Cho một hình thoi và một hình vuông có cùng chu vi. Hỏi hình nào có diện tích lớn hơn? Vì sao?
Phương pháp giải
Áp dụng:
- Công thức tính diện tích hình bình hành, hình vuông.
- Quan hệ đường xiên và hình chiếu trong tam giác vuông.
Hướng dẫn giải
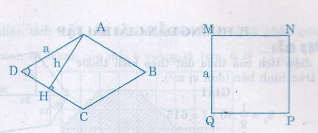
Giả sử hình thoi \(ABCD\) và hình vuông \(MNPQ\) có cùng chu vi là \(4a\).
Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài là \(a\).
Ta có: \({S_{MNPQ}} = {a^2}\)
Từ đỉnh góc tù \(A\) của hình thoi \(ABCD\) vẽ đường cao \(AH\) có độ dài \(h\).
Khi đó \({S_{ABC{\rm{D}}}} = ah\) (áp dụng công thức tính diện tích hình bình hành)
Nhưng \(h \le a\) (đường vuông góc nhỏ hơn đường xiên) nên \(ah \le {a^2}\)
Vậy \({S_{ABC{\rm{D}}}} \le {S_{MNPQ}}\)
Dấu "=" xảy ra khi \(h = a\) hay \(H\) trùng với \(D\), nghĩa là hình thoi \(ABCD\) trở thành hình vuông.