Giải bài tập SGK Toán 8 Bài 2: Định lí đảo và hệ quả của định lí Ta-lét

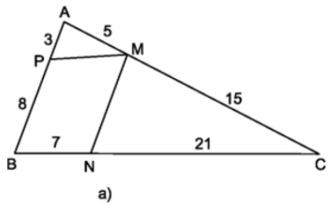
Tìm các cặp đường thẳng song song trong hình 13 và giải thích vì sao chúng song song.

Phương pháp giải

Hình a

Chứng minh 

\(\left.\begin{matrix} \dfrac{CN}{NB}=\dfrac{21}{7}=3 \\  \dfrac{CM}{MA}=\dfrac{15}{5}=3 \end{matrix}\right\} \Rightarrow \dfrac{CM}{MA}=\dfrac{CN}{NB}\)

Suy ra: \(MN // AB\)

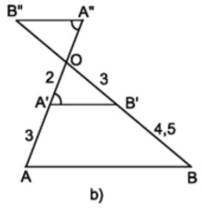
Hình b

Chứng minh \(A'B' // AB\) (1); \(A"B" // A'B'\)  (2)

Từ (1) và (2) suy ra \(AB // A'B' // A"B"\).

Hướng dẫn giải

Trên hình a ta có:

\(\dfrac{AP}{PB} = \dfrac{3}{8}\); \(\dfrac{AM}{MC}= \dfrac{5}{15} = \dfrac{1}{3}\) vì \(\dfrac{3}{8} ≠ \dfrac{1}{3}\) nên \(\dfrac{AP}{PB} ≠ \dfrac{AM}{MC}\) 

\(\Rightarrow\) \(PM\) và \(BC\) không song song. (Theo định lí Talet đảo)

Ta có \(\left.\begin{matrix} \dfrac{CN}{NB}=\dfrac{21}{7}=3 \\  \dfrac{CM}{MA}=\dfrac{15}{5}=3 \end{matrix}\right\} \Rightarrow \dfrac{CM}{MA}=\dfrac{CN}{NB}\)

 \(\Rightarrow MN // AB\) (Theo định lí TaLet đảo)

Trong hình b ta có:

Ta có: \(\dfrac{OA'}{A'A} = \dfrac{2}{3}\); \(\dfrac{OB'}{B'B} = \dfrac{3}{4,5} = \dfrac{2}{3}\) 

\(\Rightarrow \dfrac{OA'}{A'A} =  \dfrac{OB'}{B'B}\) 

\(\Rightarrow A'B' // AB\) (Theo định lí TaLet đảo)     (1)

Có \(\widehat {B''A''O} = \widehat {OA'B'}\) (gt)

Mà hai góc \(\widehat {B''A''O}\) và \( \widehat {OA'B'}\) ở vị trí so le trong

Suy ra \(A"B" // A'B'\)    (2)

Từ (1) và (2) suy ra \(AB // A'B' // A"B"\).

 Tính các độ dài \(x,y\) trong hình 14.

Phương pháp giải

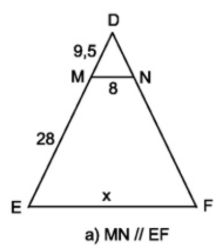
Trong hình a

\(MN // EF\), theo hệ quả định lí Ta-lét ta có: \( \dfrac{MN}{EF}=\dfrac{MD}{DE}\)

Mà \(DE = MD + ME = 9,5 + 28 = 37,5\).

\(\Rightarrow \dfrac{8}{x} = \dfrac{9,5}{37,5}\)

Suy ra x

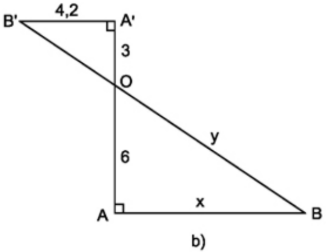
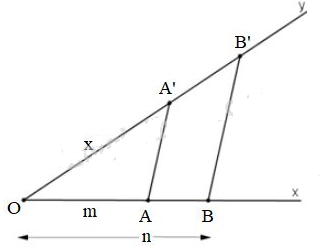
Trong hình b

Ta có \(A'B' ⊥ AA'\) (giả thiết) và \(AB ⊥ AA'\) (giả thiết)

\( \Rightarrow  A'B' // AB\) (từ vuông góc đến song song)

\( \Rightarrow \dfrac{A'O}{OA} = \dfrac{A'B'}{AB}\) (Theo hệ quả định lí Ta-let)

Hay \(\dfrac{3}{6} = \dfrac{4,2}{x}\)

Suy ra x

Xét \(∆ABO\) vuông tại \(A\) tính được y với \({y^2} = O{B^2} = O{A^2} + A{B^2}\)

Hướng dẫn giải

Trong hình a

\(MN // EF\), theo hệ quả định lí Ta-lét ta có:

\( \dfrac{MN}{EF}=\dfrac{MD}{DE}\)

Mà \(DE = MD + ME = 9,5 + 28 = 37,5\).

\(\Rightarrow \dfrac{8}{x} = \dfrac{9,5}{37,5}\)

\(\Rightarrow x= \dfrac{8.37,5}{9,5}= \dfrac{600}{19}  ≈ 31,6\)

Trong hình b

Ta có \(A'B' ⊥ AA'\) (giả thiết) và \(AB ⊥ AA'\) (giả thiết)

\( \Rightarrow  A'B' // AB\) (từ vuông góc đến song song)

\( \Rightarrow \dfrac{A'O}{OA} = \dfrac{A'B'}{AB}\) (Theo hệ quả định lí Ta-let)

Hay \(\dfrac{3}{6} = \dfrac{4,2}{x}\)

\(x = \dfrac{6.4,2}{3} = 8,4\)

\(∆ABO\) vuông tại \(A\) nên áp dụng định lý Pitago ta có:

\(\eqalign{
& {y^2} = O{B^2} = O{A^2} + A{B^2} \cr
& \Rightarrow {y^2} = {6^2} + 8,{4^2} = 106,56 \cr
& \Rightarrow y = \sqrt {106,56} \approx 10,3 \cr} \)

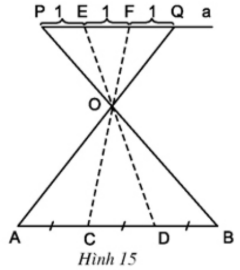
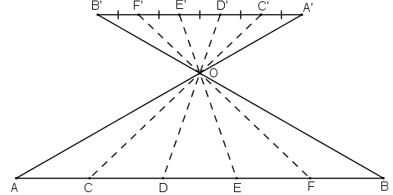
a) Để chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau, người ta đã làm như hình 15.
Hãy mô tả cách làm trên và giải thích vì sao các đoạn thẳng AC, CD, DB bằng nhau?
b) Bằng cách làm tương tự, hãy chia đoạn thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác với cách làm như trên mà vẫn có thể chia đoạn thẳng AB cho trước thành 5 đoạn thẳng bẳng nhau?

Phương pháp giải

Mô tả cách làm:

Vẽ đoạn \(PQ\) song song với \(AB, PQ\) có độ dài bằng \(3\) đơn vị

- Trên PQ lấy lần lượt các điểm E, F sao cho \(PE=EF=FQ=1\) đơn vị 

- Xác định giao điểm \(O\) của hai đoạn thẳng \(PB\) và \(QA\).

- Vẽ các đường thẳng \(EO, FO\) cắt \(AB\) tại \(C\) và \(D\).

Muốn chứng minh \(AC= CD = DB\) chỉ cần chứng minh \(\dfrac{DB}{PE} =  \dfrac{OD}{OE}\); \(\dfrac{CD}{EF} = \dfrac{OD}{OE}=\dfrac{OC}{OF}\); \(\dfrac{AC}{FQ} = \dfrac{OC}{OF}\)

b) Vẽ \(6\) đường thẳng song song cách đều nhau (có thể dùng thước kẻ để vẽ liên tiếp). Đặt đầu mút \(A\) và \(B\) ở hai đường thẳng ngoài cùng thì các đường thẳng song song cắt \(AB\) chia thành \(5\) phần bằng nhau

Hướng dẫn giải

a) Mô tả cách làm:

Vẽ đoạn \(PQ\) song song với \(AB, PQ\) có độ dài bằng \(3\) đơn vị

- Trên PQ lấy lần lượt các điểm E, F sao cho \(PE=EF=FQ=1\) đơn vị 

- Xác định giao điểm \(O\) của hai đoạn thẳng \(PB\) và \(QA\).

- Vẽ các đường thẳng \(EO, FO\) cắt \(AB\) tại \(C\) và \(D\).

Chứng minh \(AC= CD = DB\)

\(∆OPE\) và \(∆OBD\) có \(PE//DB\) (theo cách vẽ) nên \(\dfrac{DB}{PE} =  \dfrac{OD}{OE}\)     (1) (hệ quả định lý TaLet)

\(∆OEF\) và \(∆ODC\) có \(EF // CD\) (theo cách vẽ) nên \(\dfrac{CD}{EF} = \dfrac{OD}{OE}=\dfrac{OC}{OF}\)    (2) (hệ quả định lý TaLet)

\(∆OFQ\) và \(∆OCA\) có \(FQ // AC\) (theo cách vẽ) nên \(\dfrac{AC}{FQ} = \dfrac{OC}{OF}\)    (3) (hệ quả định lý TaLet)

Từ (1), (2) và (3) suy ra:

\(\dfrac{DB}{PE} = \dfrac{CD}{EF}=\dfrac{AC}{FQ}\) mà \(PE = EF=FQ\) (gt) nên \(DB = CD=AC\). 

Vây: \(DB = CD = AC\).

b) Tương tự chia đoạn thẳng \(AB\) thành \(5\) đoạn bằng nhau thực hiện như hình vẽ sau:

Cách khác: Ta có thể chia đoạn thẳng \(AB\) thành \(5\) đoạn thẳng bằng nhau như cách sau:

Vẽ \(6\) đường thẳng song song cách đều nhau (có thể dùng thước kẻ để vẽ liên tiếp). Đặt đầu mút \(A\) và \(B\) ở hai đường thẳng ngoài cùng thì các đường thẳng song song cắt \(AB\) chia thành \(5\) phần bằng nhau. 

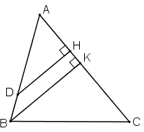
Cho tam giác \(ABC\) và điểm \(D\) trên cạnh \(AB\) sao cho \(AD= 13,5cm, DB= 4,5cm\). Tính tỉ số các khoảng cách từ điểm \(D\) và \(B\) đến cạnh \(AC\).

Phương pháp giải

Ta có \(DH // BK\) (vì cùng vuông góc với \(AC\))

\( \Rightarrow \dfrac{DH}{BK} = \dfrac{AD}{AB}\) (theo hệ quả định lý Ta Let)

Mà \(AB = AD + DB\) (giả thiết)

\( \Rightarrow  AB = 13,5 + 4,5 = 18\) (cm)

Vậy \(\dfrac{DH}{BK} = \dfrac{13,5}{18} = \dfrac{3}{4}\)

Hướng dẫn giải

Gọi \(DH\) và \(BK\) lần lượt là khoảng cách từ \(B\) và \(D\) đến cạnh \(AC\).

Ta có \(DH // BK\) (vì cùng vuông góc với \(AC\))

\( \Rightarrow \dfrac{DH}{BK} = \dfrac{AD}{AB}\) (theo hệ quả định lý Ta Let)

Mà \(AB = AD + DB\) (giả thiết)

\( \Rightarrow  AB = 13,5 + 4,5 = 18\) (cm)

Vậy \(\dfrac{DH}{BK} = \dfrac{13,5}{18} = \dfrac{3}{4}\)

Vậy tỉ số khoảng cách từ điểm \(D\) và \(B\) đến \(AC\) bằng \(\dfrac{3}{4}\)

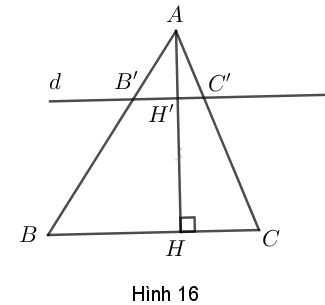
Tam giác \(ABC\) có đường cao \(AH.\) Đường thẳng \(d\) song song với \(BC\) cắt các cạnh \(AB,\, AC\) và đường cao \(AH\) theo thứ tự tại các điểm \(B', \,C'\) và \(H'\) (h.16).

a) Chứng minh rằng: \(\dfrac{AH'}{AH} = \dfrac{B'C'}{BC}\)

b) Áp dụng: Cho biết \(AH' = \dfrac{1}{3}AH\) và diện tích tam giác \(ABC\) là \(67,5 cm^2.\) Tính diện tích tam giác \(A'B'C'.\)

Phương pháp giải

a) Chứng minh \(\dfrac{B'C'}{BC} = \dfrac{AB'}{AB}\) (1); \(\dfrac{AH'}{AH} = \dfrac{AB'}{AB}\) (2)

Từ (1) và (2) \( \Rightarrow \dfrac{B'C'}{BC} = \dfrac{AH'}{AH}\)

b) Áp dụng kết quả câu a) ta có:

\(\dfrac{B'C'}{BC}= \dfrac{AH'}{AH} = \dfrac{1}{3}\)  \(\Rightarrow  B'C' = \dfrac{1}{3} BC\)

Vậy \({S_{AB'C'}} = {1 \over 2}AH'.B'C'\)

Hướng dẫn giải

a) Vì \(B'C' // BC\) \( \Rightarrow \dfrac{B'C'}{BC} = \dfrac{AB'}{AB}\)   (1) (theo hệ quả định lý TaLet)

Trong \(∆ABH\) có \(BH' // BH\) \( \Rightarrow \dfrac{AH'}{AH} = \dfrac{AB'}{AB}\)  (2) (định lý TaLet)

Từ (1) và (2) \( \Rightarrow \dfrac{B'C'}{BC} = \dfrac{AH'}{AH}\)

b) \(B'C' // BC\) mà \(AH ⊥ BC\) nên \(AH' ⊥ B'C'\) hay \(AH'\) là đường cao của \(∆AB'C'\).

 Giả thiết: \(AH' = \dfrac{1}{3} AH\).

Áp dụng kết quả câu a) ta có:

\(\dfrac{B'C'}{BC}= \dfrac{AH'}{AH} = \dfrac{1}{3}\) 

\(\Rightarrow  B'C' = \dfrac{1}{3} BC\)

\(\eqalign{
& {S_{AB'C'}} = {1 \over 2}AH'.B'C' \cr&= {1 \over 2}.{1 \over 3}AH.{1 \over 3}BC \cr 
&= {1 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& = {1 \over 9}.{S_{ABC}}\cr&= {1 \over 9}.67,5 = 7,5\,\,c{m^2} \cr} \)

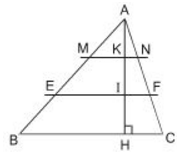
Tam giác \(ABC\) có \(BC = 15cm.\) Trên đường cao \(AH\) lấy các điểm \(I,\, K\) sao cho \(AK = KI = IH.\) Qua \(I\) và \(K\) vẽ các đường \(EF // BC,\, MN // BC\) (h.17).

a) Tính độ dài các đoạn thẳng \(MN\) và \(EF.\)

b) Tính diện tích tứ giác \(MNFE,\) biết rằng diện tích của tam giác \(ABC\) là \(270cm^2.\)

Phương pháp giải

a) \(∆ABC\) có \(MN // BC\) (gt) \( \Rightarrow \dfrac{MN}{CB} = \dfrac{AK}{AH}\)

Chứng minh và suy ra \(MN = \dfrac{1}{3}BC\)

(∆ABC\) có \(EF // BC\) (gt) \( \Rightarrow \dfrac{EF}{BC} = \dfrac{AI}{AH} = \dfrac{2}{3}\)

\(\Rightarrow  EF =\dfrac{2}{3}.BC\)

b) Ta có: \({S_{AMN}} = {1 \over 2}.AK.MN\); \({S_{AEF}} = {1 \over 2}.AI.EF\)

Do đó \({S_{MNFE}} = {S_{AEF}} - {S_{AMN}}

Hướng dẫn giải

a) \(∆ABC\) có \(MN // BC\) (gt)

\( \Rightarrow \dfrac{MN}{CB} = \dfrac{AK}{AH}\) (kết quả bài tập 10) (định lý TaLet)

Mà \(AK = KI = IH\).

Nên \(\dfrac{AK}{AH} = \dfrac{1}{3}\) 

\( \Rightarrow \dfrac{MN}{CB} = \dfrac{1}{3}\) 

\( \Rightarrow  MN = \dfrac{1}{3}BC = \dfrac{1}{3}.15 = 5\, cm\).

\(∆ABC\) có \(EF // BC\) (gt)

\( \Rightarrow \dfrac{EF}{BC} = \dfrac{AI}{AH} = \dfrac{2}{3}\) (định lý TaLet)

\(\Rightarrow  EF =\dfrac{2}{3}.BC= \dfrac{2}{3}.15 =10 \,cm\).

b) Theo câu a) ta có: \(AK=\dfrac{1}{3}AH;MN=\dfrac{1}{3}BC;\) \(AI=\dfrac{2}{3}AH;EF=\dfrac{2}{3}BC\)

Nên:

\(\eqalign{
& {S_{AMN}} = {1 \over 2}.AK.MN \cr 
&= {1 \over 2}.{1 \over 3}AH.{1 \over 3}BC \cr 
& = {1 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
& = {1 \over 9}.{S_{ABC}} \cr 
& = {1 \over 9}.270 = 30\,c{m^2} \cr} \)

\(\eqalign{
& {S_{AEF}} = {1 \over 2}.AI.EF \cr 
&= {1 \over 2}.{2 \over 3}AH.{2 \over 3}BC \cr 
& = {4 \over 9}.\left( {{1 \over 2}AH.BC} \right) \cr 
&= {4 \over 9}.{S_{ABC}} \cr 
&= {4 \over 9}.270 = 120\,c{m^2} \cr} \)

Do đó \({S_{MNFE}} = {S_{AEF}} - {S_{AMN}} = 120 - 30 \)\(\,= 90c{m^2}\)

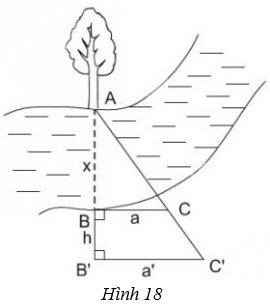
Có thể đo dược chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?

Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tình chiều rộng của khúc sông mà không cần phải sang bờ bên kia(h18). Nhìn hình vẽ, Hãy mô tả những công việc cần làm và tính khoảng cách \(AB = x\) theo \(BC = a, B'C'= a', BB'= h\).

Phương pháp giải

Ta có: \(BC ⊥ AB’\) và \(B’C’ ⊥ AB’ ⇒ BC // B’C’\)

Xét \(ΔAB’C’\) có \(BC // B’C’ \,(B ∈ AB’, C ∈ AC’) \) 

\(⇒ \dfrac{AB}{AB'} = \dfrac{BC}{BC'}\) (hệ quả định lý Talet) mà \(AB' = x + h\) nên 

\(\dfrac{x}{x+ h} = \dfrac{a}{a'}\) 

\( \Leftrightarrow  a'x = ax + ah\)

Suy ra \(x= \dfrac{ah}{a'-a}\)

Hướng dẫn giải

Mô tả cách làm:

* Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và \(AB\) chính là khoảng cách cần đo.

* Trên hai đường thẳng vuông góc với \(AB'\) tại \(B\) và \(B'\) lấy \(C\) và \(C'\) sao cho \(A,C,C'\) thẳng hàng.

* Đo độ dài các đoạn \(BB'= h, BC= a, B'C'= a'\). Từ đó ta sẽ tính được đoạn \(AB=x.\)

Bài giải

Ta có: \(BC ⊥ AB’\) và \(B’C’ ⊥ AB’ ⇒ BC // B’C’\)

Xét \(ΔAB’C’\) có \(BC // B’C’ \,(B ∈ AB’, C ∈ AC’) \) 

\(⇒ \dfrac{AB}{AB'} = \dfrac{BC}{BC'}\) (hệ quả định lý Talet) mà \(AB' = x + h\) nên 

\(\dfrac{x}{x+ h} = \dfrac{a}{a'}\) 

\( \Leftrightarrow  a'x = ax + ah\)

\( \Leftrightarrow  a'x - ax = ah\)

\(\Leftrightarrow  x(a' - a) = ah\)

\( \Rightarrow x= \dfrac{ah}{a'-a}\)

Vậy khoảng cách \(AB\) bằng \(\dfrac{ah}{a'-a}\)

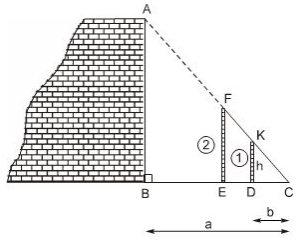
Có thể đo gián tiếp chiều cao của một bức tường bằng dụng cụ đo đơn giản được không?

Hình 19: thể hiện cách đo chiều cao \(AB\) của một bức tường bằng các dụng cụ đơn giản gồm:

Hai cọc thẳng đứng và sợi dây \(FC\), Cọc 1 có chiều cao \(DK= h\). Các khoảng cách \(BC= a, DC= b\) đo được bằng thước thông dụng.

a) Em hãy cho biết người ta tiến hành đo đạc như thế nào ? 

b) Tính chiều cao \(AB\) theo \(h, a, b\).

Phương pháp giải

a) Cách tiến hành:

- Đặt hai cọc thẳng đứng, di chuyển cọc \(2\) sao cho \(3\) điểm \(A,F,K\) nằm trên một đường thẳng.

- Dùng sợi dây căng thẳng qua \(2\) điểm \(F\) và \(K\) để xác định điểm \(C\) trên mặt đất (\(3\) điểm \(F,K,C\) thẳng hàng).

b) \(∆ABC\) có \(AB // DK\) nên \(\dfrac{DK}{AB} = \dfrac{DC}{BC}\) 

\( \Rightarrow  AB = \dfrac{DK.BC}{DC}\)

Hướng dẫn giải

a) Cách tiến hành:

- Đặt hai cọc thẳng đứng, di chuyển cọc \(2\) sao cho \(3\) điểm \(A,F,K\) nằm trên một đường thẳng.

- Dùng sợi dây căng thẳng qua \(2\) điểm \(F\) và \(K\) để xác định điểm \(C\) trên mặt đất (\(3\) điểm \(F,K,C\) thẳng hàng).

b) \(∆ABC\) có \(AB // DK\) nên \(\dfrac{DK}{AB} = \dfrac{DC}{BC}\) 

\( \Rightarrow  AB = \dfrac{DK.BC}{DC} = \dfrac{h.a}{b}\) (theo hệ quả định lí Talet)

Vậy chiều cao của bức tường \( AB = \dfrac{h.a}{b}\).

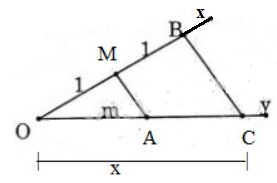
Cho ba đoạn thẳng có độ dài là \(m,\, n,\, p\) (cùng đơn vị đo).

Dựng đoạn thẳng có độ dài \(x\) sao cho:

a) \(\dfrac{x}{m} = 2\)

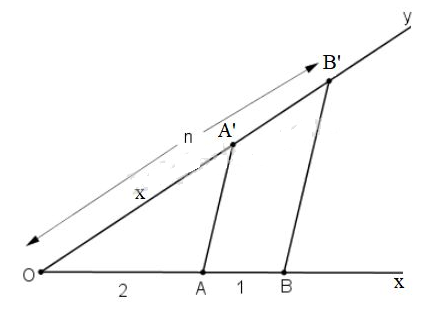
b) \(\dfrac{x}{n} = \dfrac{2}{3}\)

c) \( \dfrac{m}{x} = \dfrac{n}{p}\)

Có \(OA' = x.\)

Phương pháp giải

a) Xét tam giác OBC có \(MN//BC\) nên: \(\dfrac{OC}{OA} = \dfrac{OB}{OM}\)

\( \Rightarrow \dfrac{x}{m} = 2\)

b) Xét tam giác OBB' có: \(AA' // BB'\)

\(\Rightarrow \dfrac{OA'}{OB'} = \dfrac{OA}{OB}\)

Hay \(\dfrac{x}{n} = \dfrac{2}{3}\) 

c) Xét tam giác OBB' có \(AA' // BB'\)

\(\Rightarrow \dfrac{OA}{OA'} = \dfrac{OB}{OB'}\) hay \(\dfrac{m}{x} = \dfrac{n}{p}\)

Hướng dẫn giải

a) Cách dựng:

- Vẽ hai tia \(Ox, Oy\) không đối nhau.

- Trên tia \(Ox\) lấy hai điểm \(M,\,B\) sao cho \(OM =1;OB=2\) đơn vị.

- Trên tia \(Oy\) lấy điểm A sao cho \(OA=m\) 

- Nối \(MA\).

- Vẽ đường thẳng đi qua \(B\) và song song với \(MA\) cắt \(Oy\) tại \(C\) thì \(OC=x\) là đoạn thẳng cần dựng.

Chứng minh: 

Xét tam giác OBC có \(MN//BC\) nên:

\(\dfrac{OC}{OA} = \dfrac{OB}{OM}\) (theo hệ quả định lí Talet)

\( \Rightarrow \dfrac{x}{m} = 2\)

b) Cách dựng: 

- Vẽ hai tia \(Ox\) và \(Oy\) không đối nhau.

- Trên tia \(Ox\) đặt hai đoạn \(OA= 2\) đơn vị, \(OB= 3\) đơn vị.

- Trên tia \(Oy\) đặt đoạn \(OB' = n\)

- Nối \(BB'\)

- Vẽ đường thẳng qua \(A\) song song với \(BB'\) cắt \(Oy\) tại \(A'\) và đặt \(OA' = x\).

Khi đó OA' là đoạn thẳng cần dựng.

Chứng minh:

Xét tam giác OBB' có: \(AA' // BB'\)

\(\Rightarrow \dfrac{OA'}{OB'} = \dfrac{OA}{OB}\) (theo hệ quả định lí Talet)

hay \(\dfrac{x}{n} = \dfrac{2}{3}\) 

c) 

Cách dựng:

- Vẽ tia \(Ox, Oy\) không đối nhau.

- Trên tia \(Ox\) đặt đoạn \(OA= m, OB= n\).

- Trên tia \(Oy\) đặt đoạn \(OB' = p\).

- Vẽ đường thẳng qua \(A\) và song song với \(BB'\) cắt \(Oy\) tại \(A'\) thì \(OA' = x\) là đoạn thẳng cần dựng.

Chứng minh:

Xét tam giác OBB' có \(AA' // BB'\)

\(\Rightarrow \dfrac{OA}{OA'} = \dfrac{OB}{OB'}\) (theo hệ quả định lí Talet) hay \(\dfrac{m}{x} = \dfrac{n}{p}\)