Giải bài tập SGK Toán 8 Bài 1: Tứ giác

Phương pháp giải

Áp dụng định lý: Tổng các góc của một tứ giác bằng $360^0.$

Hướng dẫn giải

Ở hình 5

a) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $ABCD$ ta được:

$\eqalign{ & \,\,\widehat A + \widehat B + \widehat C + \widehat D = {360^0} \cr & \Rightarrow \widehat D = {360^0} - \left( {\,\,\widehat A + \widehat B + \widehat C} \right) \cr & \Rightarrow x = {360^0} - \left( {{{110}^0} + {{120}^0} + {{80}^0}} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {310^0} = {50^0} \cr}$

b) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $EFGH$ ta được:

$\eqalign{ & \widehat E + \widehat F + \widehat G + \widehat H = {360^0} \cr & \Rightarrow \widehat G = {360^0} - \left( {\widehat E + \widehat F + \widehat H} \right) \cr & \Rightarrow x = {360^0} - \left( {{{90}^0} + {{90}^0} + {{90}^0}} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {270^0} = {90^0} \cr}$

c) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $ABDE$ ta được:

$\eqalign{ & \widehat A + \widehat B + \widehat D + \widehat E = {360^0} \cr & \Rightarrow \widehat D = {360^0} - \left( {\widehat A + \widehat B + \widehat E} \right) \cr & \Rightarrow x = {360^0} - \left( {{{65}^0} + {{90}^0} + {{90}^0}} \right) \cr & \;\,\,\,\,\,\,\,\,\,\, = {360^0} - {245^0} = {115^0} \cr}$

d) Ta có: $\widehat {IKM}+60^0=180^0$ (hai góc kề bù) $\Rightarrow \widehat {IKM} = {180^0} - {60^0} = {120^0}$

$\widehat {KMN}+105^0=180^0$ (hai góc kề bù) $\Rightarrow \widehat {KMN} = {180^0} - {105^0} = {75^0}$

Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $MNIK$ ta được:

$\eqalign{ & \widehat {KMN} + \widehat {MNI} + \widehat {NIK} + \widehat {IKM} = {360^0} \cr & \Rightarrow \widehat {MNI} = {360^0} - \left( {\widehat {KMN} + \widehat {IKM} + \widehat {NIK}} \right) \cr & \Rightarrow x = {360^0} - \left( {{{75}^0} + {{120}^0} + {{90}^0}} \right) \cr & \,\,\,\,\,\,\,\,\,\,\,\, = {360^0} - {285^0} = {75^0} \cr}$

Ở hình 6

a) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $PQRS$ ta được:

$\eqalign{ & \widehat P + \widehat Q + \widehat R + \widehat S = {360^0} \cr & \Rightarrow \widehat P + \widehat Q = {360^0} - \left( {\widehat S + \widehat R} \right) \cr & \Rightarrow x + x = {360^0} - \left( {{{65}^0} + {{95}^0}} \right) \cr & \Rightarrow 2x = {360^0} - {160^0} \cr & \Rightarrow x = {{{{360}^0} - {{160}^0}} \over 2} \cr & \Rightarrow x = {{{{200}^0}} \over 2} \cr & \Rightarrow x = {100^0} \cr}$

b) Áp dụng định lí tổng các góc của một tứ giác vào tứ giác $MNPQ$ ta được:

$\eqalign{ & \widehat M + \widehat N + \widehat P + \widehat Q = {360^0} \cr & 3x + 4x + x + 2x = {360^0} \cr & 10x = {360^0} \cr & x = {{{{360}^0}} \over {10}} = {36^0} \cr}$

Góc kề bù với một góc của tứ giác gọi là góc ngoài của tứ giác

a) Tính các góc ngoài của tứ giác ở hình 7a

b) Tính tổng các góc ngoài của tứ giác ở hình 7b ( tại mỗi đỉnh của tứ giác chỉ chọn một góc ngoài):

$\widehat{A_1} + \widehat{B_1} + \widehat{C_1} + \widehat{D_1} = ?$

c) Có nhận xét gì về tổng các góc ngoài của tứ giác?

Phương pháp giải

Áp dụng định lý: Tổng các góc trong tứ giác bằng ${360^0}$

Hướng dẫn giải

Câu a: $\widehat A + \widehat B + \widehat C + \widehat D = {360^0}$ (định lý tổng các góc của tứ giác)

$\begin{array}{l} \widehat {{D}}= {360^0} - \left( {\widehat A + \widehat B + \widehat C} \right)\\ = {360^0} - \left( {{75}^0+{{90}^0} + {{120}^0}} \right)\\ = {360^0} - {285^0}\\= {75^0} \end{array}$

Ta có

$\widehat {BAD} + \widehat {{A_1}} = {180^0}$ (2 góc kề bù)

$\begin{array}{l} \widehat {{A_1}} = {180^0} - \widehat {BAD}\\ = {180^0} - {75^0} = {105^0}. \end{array}$

$\widehat {{B_1}} + \widehat {CBA} = {180^0}$ (2 góc kề bù)

$\begin{array}{l} \widehat {{B_1}} = {180^0} - \widehat {CBA}\\= {180^0} - {90^0} = {90^0}. \end{array}$

$\widehat {{C_1}} + \widehat {BCD} = {180^0}$ (2 góc kề bù)

$\begin{array}{l} \widehat {{C_1}} = {180^0} - \widehat {BC{\rm{D}}}\\= {180^0} - {120^0} = {60^0}. \end{array}$

$\widehat {{D_1}} + \widehat {ADC} = {180^0}$

$\begin{array}{l} \widehat {{D_1}} = {180^0} - \widehat {{\rm{ADC}}}\\= {180^0} - {75^0} = {105^0}. \end{array}$

Câu b

Ta có

$\widehat {A} + \widehat {{A_1}} = {180^0}$ (2 góc kề bù) $\Rightarrow \widehat {{A_1}} = {180^0}-\widehat {A}$

$\widehat {B} + \widehat {{B_1}} = {180^0}$ (2 góc kề bù) $\Rightarrow \widehat {{B_1}} = {180^0}-\widehat {B}$

$\widehat {C} + \widehat {{C_1}} = {180^0}$ (2 góc kề bù) $\Rightarrow \widehat {{C_1}} = {180^0}-\widehat {C}$

$\widehat {D} + \widehat {{D_1}} = {180^0}$ (2 góc kề bù) $\Rightarrow \widehat {{D_1}} = {180^0}-\widehat {D}$

Lại có: $\widehat {{A}} + \widehat {{B}} + \widehat {{C}} + \widehat {{D}} = {360^0}$ (định lý tổng 4 góc trong tứ giác ABCD)

Ta có 

$\begin{array}{l} \widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} + \widehat {{D_1}}\\ = \left( {{{180}^0} - \widehat {{A}}} \right) + \left( {{{180}^0} - \widehat {{B}}} \right) \\\;\;\;+ \left( {{{180}^0} - \widehat {{C}}} \right) + \left( {{{180}^0} - \widehat {{D}}} \right)\\ = {180^0}.4 - \left( {\widehat {{A}} + \widehat {{B}} + \widehat {{C}} + \widehat {{D}}} \right)\\ = {720^0} - {360^0} = {360^0}. \end{array}$

Câu c: Nhận xét: Tổng các góc ngoài của tứ giác bằng ${360^0}$ 

Ta gọi tứ giác ABCD trên hình 8 có AB = AD, CB = CD là hình "cái diều"

a) Chứng minh rằng AC là đường trung trực của BD.

b) Tính $\widehat{B}, \widehat{D}$ biết rằng $\widehat{A}= 100^0$ và $\widehat{C}= 60^0$ .

Phương pháp giải

Áp dụng: Tính chất: Một điểm thuộc đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.

Hướng dẫn giải

Câu a: Ta có: $AB = AD$ (giả thiết) $\Rightarrow  A$ thuộc đường trung trực của $BD$ (Theo tính chất một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó).

$CB = CD$ (giả thiết) $\Rightarrow  C$ thuộc đường trung trực của $BD$ (Theo tính chất một điểm cách đều hai đầu của đoạn thẳng thì thuộc đường trung trực của đoạn thẳng đó).

Vậy $AC$ là đường trung trực của $BD.$

Câu b: Tính $\widehat B;\widehat D$ biết rằng $\widehat A = {100^0};\widehat C = {60^0}$

Xét $∆ ABC$ và $∆ADC$ có:

$AB = AD$ (giả thiết)

$BC = DC$ (giả thiết)  

$AC$ cạnh chung

Suy ra $∆ ABC = ∆ADC$ (c.c.c) 

$\Rightarrow \widehat B = \widehat D$ (hai góc tương ứng)

Xét tứ giác $ABCD$, ta có: $\widehat B + \widehat {BC{\rm{D}}} + \widehat {\rm{D}} + \widehat {BA{\rm{D}}} = {360^0}$ (Định lí tổng các góc của một tứ giác).

$\begin{array}{l} \Rightarrow \widehat B + \widehat {\rm{D}} = {360^0} - \left( {\widehat {BC{\rm{D}}} + \widehat {BA{\rm{D}}}} \right) \\\;\;\;\;\;\;\;\;\;\;\;= {360^0} - \left( {{{60}^0} + {{100}^0}} \right) = {200^0}\\ \text{Mà  }\widehat B= \widehat D\text{ (chứng minh trên) }\\ \Rightarrow \widehat B+\widehat B = {200^0}\\\Rightarrow 2\widehat B = 200^0 \end{array}$

Vậy $\widehat B = \widehat {\rm{D}} = {200^0}:2 = {100^0}.$

Dựa vào cách vẽ các tam giác đã học, hãy vẽ lại các tứ giác ở hình 9, hình 10 vào vở.

Phương pháp giải

Áp dụng cách vẽ tam giác biết độ dài $3$ cạnh, $2$ cạnh và $1$ góc xen giữa.

Hướng dẫn giải

Cách vẽ hình $9$

Vẽ $\Delta ABC$ trước rồi vẽ $\Delta ACD$ (hoặc ngược lại).

- Vẽ đoạn thẳng $AC = 3cm$.

- Trên cùng một nửa mặt phẳng bờ $AC$, vẽ cung tròn tâm $A$ bán kính $1,5cm$ với cung tròn tâm $C$ bán kính $2cm$.

- Hai cung tròn trên cắt nhau tại $B$.

- Vẽ các đoạn thẳng $AB, AC$ ta được $\Delta ABC$.

- Trên cùng một nửa mặt phẳng bờ $AC$ không chứa $B$, vẽ cung tròn tâm $A$ bán kính $3cm$ với cung tròn tâm $C$ bán kính $3,5cm$.

- Hai cung tròn trên cắt nhau tại $D$.

- Vẽ các đoạn thẳng $AD,AC$ ta được $\Delta ADC$.

Tứ giác $ABCD$ là tứ giác cần vẽ.

Cách vẽ hình 10

Vẽ $\Delta MQP$ trước rồi vẽ $\Delta MNP$.

Vẽ $\Delta MQP$ biết hai cạnh và góc xen giữa.

- Vẽ góc $\widehat{xQy}=70^{0}$

- Trên tia $Qy$ lấy điểm $M$ sao cho $QM = 2cm.$

- Trên tia $Qx$ lấy điểm $P$ sao cho $QP = 4cm.$  

- Vẽ đoạn thẳng $MP$, ta được $\Delta MQP$.

Vẽ $\Delta MNP$ biết ba cạnh, với cạnh $MP$ đã vẽ.

- Trên cùng một nửa mặt phẳng bờ $MP$ không chứa $Q$, vẽ cung tròn tâm $M$ bán kính $1,5cm$ và cung tròn tâm $P$ bán kính $3cm$.

- Hai cung tròn trên cắt nhau tại $N.$

- Vẽ các đoạn thẳng $MN$, $PN$ ta được $\Delta MNP$.

Tứ giác $MNPQ$ là tứ giác cần vẽ

Đố. Đố em tìm thấy vị trí của "kho báu" trên hình 11, biết rằng kho báu nằm tại giao điểm các đường chéo của tứ giác ABCD, trong đó các đỉnh của tứ giác có tọa độ như sau: A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5).

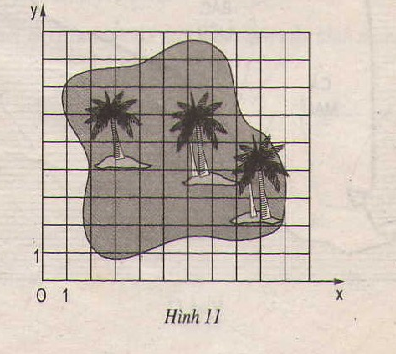
Phương pháp giải

Áp dụng cách xác định tọa độ của một điểm trên hệ trục tọa độ $Oxy.$

Hướng dẫn giải

Các bước làm như sau

- Xác định các điểm $A, B, C, D$ trên hình vẽ với $A(3 ; 2), B(2 ; 7), C(6 ; 8), D(8 ; 5)$.

- Vẽ tứ giác $ABCD.$

- Vẽ hai đường chéo $AC$ và $BD$. Gọi $K$ là giao điểm của hai đường chéo đó.

- Xác định tọa độ của điểm $K$ là $K(5 ; 6)$

Vậy vị trí kho báu có tọa độ $K(5 ; 6)$ trên hình vẽ