Giải bài tập SGK Toán 8 Bài 5: Diện tích xung quanh của hình lăng trụ đứng

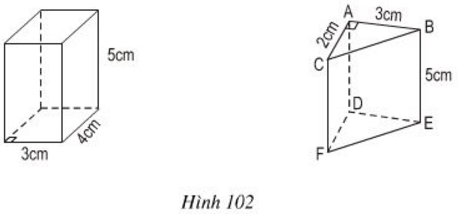
Tính diện tích xung quanh, diện tích toàn phần của các lăng trụ đứng sau đây (h.102):

Phương pháp giải

- Tính diện tích xung quanh hình lăng trụ đứng theo công thức: $S_{xq} = 2p.h$ với $p$ là nửa chu vi đáy, $h$ là chiều cao lăng trụ.

- Diện tích toàn phần = diện tích xung quanh + diện tích hai đáy. 

Hướng dẫn giải

a) Với hình vẽ bên trái

Diện tích xung quanh của lăng trụ đứng là: 

$2.(3+ 4) . 5 = 70 (cm^2)$

Diện tích toàn phần của lăng trụ đứng là:

$70 + 2.3.4. = 94(cm^2)$

b) Với hình vẽ bên phải: 

$\triangle ABC$ vuông tại  $A \Rightarrow BC^2 = AB^2 + AC^2 = 9 + 4 = 13$

$\Rightarrow BC = \sqrt{13} (cm)$

Nửa chu vi đáy là: $\dfrac{2+3+\sqrt {13}}{2}=\dfrac{5+\sqrt {13}}{2}$

Diện tích xung quanh của lăng trụ đứng là:

$2.\dfrac{5+\sqrt {13}}{2}.5 = 25 + 5\sqrt{13}  (cm^2 )$

Diện tích toàn phần của lăng trụ đứng là:

$25 + 5\sqrt{13} + 2(\dfrac{1}{2}. 2.3)$

$= 25 + 5\sqrt{13} + 6= 31 + 5\sqrt{13}(cm^2 )$ 

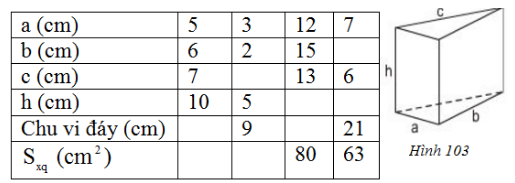
Quan sát lăng trụ đứng tam giác rồi điền số thích hợp vào các ô trống ở bảng sau

Phương pháp giải

Dựa vào công thức tính diện tích xung quanh hình lăng trụ đứng: $S_{xq} = 2p.h$ với $p$ là nửa chu vi đáy, $h$ là chiều cao lăng trụ.

+ Chu vi đáy $C= a + b + c$ (kí hiệu C là chu vi đáy)

+ Diện tích xung quanh = chu vi đáy x chiều cao

Hướng dẫn giải

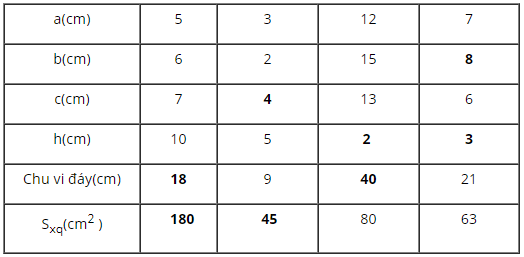
Cột 1:

Chu vi đáy là: $C=5+6+7=18 \;cm$

${S_{xq}} = 18.10 = 180\;cm^2$

Cột 2:

Độ dài cạnh thứ 3 của tam giác đáy là $c=9-3-2=4$

${S_{xq}} = 9.5 = 45\;cm^2$

Cột 3:

Chu vi đáy là $C=12+15+13=40\;cm$

Chiều cao là: $h = \dfrac{{{S_{xq}}}}{{C}} = \dfrac{{80}}{{40}} = 2\;cm$

Cột 4:

Độ dài cạnh còn lại của tam giác đáy là: $b=21-7-6=8\;cm$

Chiều cao là: $h = \dfrac{{{S_{xq}}}}{C} = \dfrac{{63}}{{21}} = 3\;cm$ 

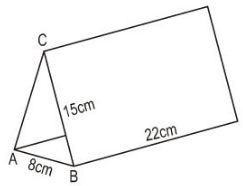
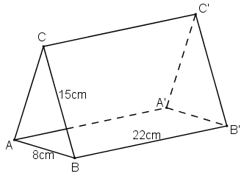
Tấm lịch để bàn (xem lại hình 94) có dạng một lăng trụ đứng, ABC là một tam giác cân (h.104).

a) Hãy vẽ thêm nét khuất, điền thêm chữ vào các đỉnh rồi cho biết AC song song với những cạnh nào?

b) Tính diện tích miếng bìa dùng để làm một tấm lịch như trên.

Phương pháp giải

- Diện tích miếng bìa dùng để làm tấm lịch như trên chính là diện tích xung quanh của lăng trụ đứng có đáy là một tam giác cân.

- Tính diện tích xung quanh hình lăng trụ đứng bằng tích của chu vi đáy và chiều cao. 

- Chu vi tam giác bằng tổng độ dài ba cạnh của tam giác đó.

Hướng dẫn giải

a) 

Cạnh $AC$ song song với cạnh $A’C’.$

b) Diện tích miếng bìa dùng để làm tấm lịch như trên là diện tích xung quanh của lăng trụ đứng.

Tam giác $ABC$ là tam giác cân tại C nên $AC=BC=15cm$

Chu vi tam giác $ABC$ là:

$15.2+8=38\;cm$

Diện tích xung quanh của lăng trụ đứng như trên là:  

$38. 22 = 836\;(cm^2 )$

Vậy diện tích miếng bìa dùng để làm một tấm lịch như trên là  $836cm^2$.

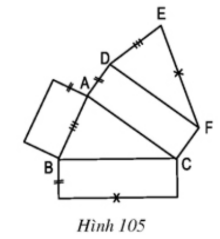
a) Từ hình khai triển (h.105) có thể gấp theo các cạnh để có được một tấm lăng trụ đứng hay không ? (Các tứ giác trên hình đều là hình chữ nhật).

b) Trong các hình vừa gấp được, xét xem các phát biểu dưới đây, phát biểu nào đúng ?

- Cạnh $AD$ vuông góc với cạnh $AB$.

- $EF$ và $CF$ là hai cạnh vuông góc với nhau.

- Cạnh $DE$ và cạnh $BC$ vuông góc với nhau.

- Hai đáy $(ABC)$ và $(DEF)$ nằm trên hai mặt phẳng song song với nhau.

- Mặt phẳng $(ABC)$ song song với mặt phẳng $(ACFD)$.

Phương pháp giải

Sử dụng định nghĩa:

- Hai đường thẳng vuông góc: Hai đường thẳng $xx'$ và $yy'$ cắt nhau, nếu trong các góc tạo thành có một góc vuông thì hai đường thẳng đó gọi là hai đường thẳng vuông góc và kí hiệu $xx'\perp yy'$.

- Hai mặt phẳng song song: Nếu mặt phẳng $(ABCD)$ chứa hai đường thẳng $a$ và $b$ cắt nhau mà song song với hai đường thẳng $a'$ và $b'$ chứa trong mặt phẳng $(A'B'C'D')$ thì ta nói hai mặt phẳng $(ABCD)$ và $(A'B'C'D')$ song song nhau

Hướng dẫn giải

a) Từ hình khai triển bên, ta có thể gấp theo các cạnh để được hình lăng trụ đứng.

b) Các phát biểu đúng:

- Cạnh $AD$ vuông góc với cạnh $AB$.

- $EF$ và $CF$ là hai cạnh vuông góc với nhau.

- Hai đáy $(ABC)$ và $(DEF)$ nằm trên hai mặt phẳng song song với nhau.