Giải bài tập SGK Toán 8 Bài 3: Diện tích tam giác

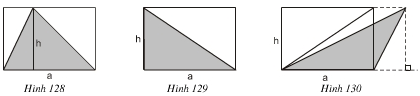
Giải thích vì sao diện tích của tam giác được tô đậm trong các hình 128,129, 130 bằng nửa diện tích hình chữ nhật tương ứng:

Phương pháp giải

Áp dụng công thức tính diện tích hình chữ nhật, diện tích tam giác.

Hướng dẫn giải

Ở mỗi hình \(128, 129, 130\): Các hình tam giác tô đậm đều có đáy \(a\) và chiều cao \(h\), các hình chữ nhật đều có hai kích thước là \(h\) và \(a\).

- Diện tích hình chữ nhật là \(a.h\)

- Diện tích tam giác  là \(\dfrac{{a.h}}{2}\)

Vậy diện tích của tam giác bằng nửa diện tích hình chữ nhật tương ứng

Cho tam giác AOB vuông tại O với đường cao OM (h.131). Hãy giải thích vì sao ta có đẳng thức: AB. OM = OA. OB.

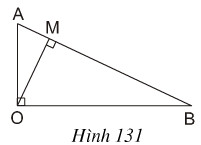
Phương pháp giải

Áp dụng cách tính diện tích tam giác thường và tam giác vuông.

Hướng dẫn giải

Ta có cách tính diện tích tam giác \(AOB\) với đường cao \(OM\) và cạnh đáy \(AB:\)

\(S = \dfrac{{OM.AB}}{2}\) 

Ta lại có cách tính diện tích tam giác \(AOB\) vuông với hai cạnh góc vuông \(OA, OB\) là

\(S = \dfrac{{OA.OB}}{2}\)

\( \Rightarrow \dfrac{{OM.AB}}{2} = \dfrac{{OA.OB}}{2}\,(=S)\)

\(\Rightarrow OM.AB = OA.OB.\)

Cho tam giác ABC và đường trung tuyến AM(h. 132). Chứng minh rằng: SAMB = SAMC

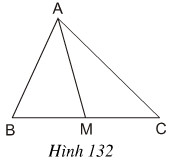
Phương pháp giải

- Dựng \(AH\) là đường cao của \(\Delta ABC\).

- Áp dụng công thức tính diện tích tam giác.

Hướng dẫn giải

Dựng \(AH\) là đường cao của \(\Delta ABC\), khi đó \(\Delta ABM,\Delta AMC\) có chung chiều cao \(AH\).

Ta có:

\({S_{AMB}} = \dfrac{1}{2}BM.AH\) (chiều cao \(AH\) và cạnh đáy \(BM\)) 

\({S_{AMC}} = \dfrac{1}{2}CM.AH\) (chiều cao \(AH\) và cạnh đáy \(CM\)) 

Mà \(BM = CM\) (vì \(AM\) là đường trung tuyến)

Vậy  \({S_{AMB}} = {S_{AMC}}.\)

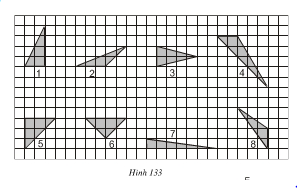
a) Xem hình 133. Hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích)

b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?

Phương pháp giải

Đếm số ô vuông và áp dụng công thức tính diện tích tam giác.

Hướng dẫn giải

Câu a

Các tam giác số \(1, 3, 6\) có cùng diện tích là \(4\) ô vuông.

Các tam giác số \(2, 8\) có cùng diện tích là \(3\) ô vuông.

Các tam giác số \(4, 5, 7\) không có cùng diện tích với các tam giác nào khác (diện tích tam giác số \(4\) là \(5\) ô vuông, tam giác số \(5\) là \(4,5\) ô vuông, tam giác số \(7\) là \(3,5\) ô vuông).

Câu b

Hai tam giác có diện tích bằng nhau thì chưa chắc hai tam giác đó đã bằng nhau.

Vì diện tích của tam giác là nửa tích của độ dài đáy với chiều cao tương ứng của đáy, nên chỉ cần tích của đáy với chiều cao bằng nhau thì hai tam giác đó có diện tích bằng nhau, hai cạnh còn lại có thể khác nhau.

- Ví dụ như các tam giác \(1, 3, 6\) có cùng diện tích nhưng không bằng nhau.

Vẽ hình chữ nhật có một cạnh bằng một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.

Phương pháp giải

Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

Hướng dẫn giải

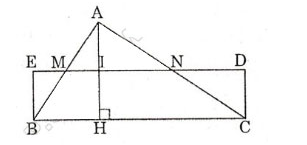
Cho tam giác \(ABC\) với đường cao \(AH\)

Gọi \(M, N, I\) là trung điểm của \(AB, AC, AH.\)

Lấy \(E\) đối xứng với \(I\) qua \(M, D\) đối xứng với \(I\) qua \(N.\)

\(⇒\) Hình chữ nhật \(BEDC\) là hình cần dựng.

Thật vậy: 

Vì \(E\) đối xứng với \(I\) qua \(M\) nên \(M\) là trung điểm của \(EI\)

Do đó, \(EM=MI\)

Xét hai tam giác \(∆EBM\) và \(∆IAM\) có:

+) \(MA=MB\) (do M là trung điểm của AB) 

+) \(\widehat {BME} = \widehat {AMI}\) (đối đỉnh)

+) \(EM=MI\) (chứng minh trên)

\( \Rightarrow ∆EBM = ∆IAM\) ( c-g-c)

\( \Rightarrow {S_{IAM}} = {S_{EBM}}\)

Vì \(D\) đối xứng với \(I\) qua \(N\) nên \(N\) là trung điểm của \(DI\)

Do đó, \(NI=ND\)

Xét hai tam giác \(∆IAN\) và \(∆DCN\) có:

+) \(IN=ND\) (chứng minh trên)

+) \(\widehat {ANI} = \widehat {DNC}\) (đối đỉnh)

+) \(AN = NC \) (do N là trung điểm của AC)

\( \Rightarrow ∆IAN = ∆DCN\) ( c-g-c)

\( \Rightarrow {S_{DCN}} = {S_{IAN}}\)

Ta có: 

\({S_{BEM}} + {S_{BMNC}} + {S_{N{\rm{D}}C}} = {S_{AMI}} \)\(+ {S_{BMNC}} + {S_{AIN}}\)

\(\Rightarrow {S_{ABC}}={S_{EB{\rm{D}}C}} \)\( =BE.BC= \dfrac{1}{2}AH.BC \) (vì \(BE=IH=\dfrac{AH}2)\)

Ta đã tìm được công thức tính diện tích tam giác bằng một phương pháp khác. 

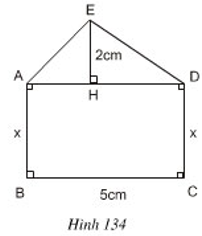
Tính \(x\) sao cho diện tích hình chữ nhật \(ABCD\) gấp \(3\) lần diện tích \(∆ADE\) (h.\(134\))

Phương pháp giải

Áp dụng: Công thức tính diện tích tam giác, diện tích hình chữ nhật, biểu diễn diện tích hình chữ nhật theo diện tích của \(∆ADE\).

Hướng dẫn giải

Ta có: \(AD = BC = 5cm\) (vì \(ABCD\) là hình chữ nhật)

Diện tích  \(∆ADE\) là: \({S_{ADE}} = \dfrac{{EH.A{\rm{D}}}}{2} = \dfrac{{2.5}}{2} = 5\;(c{m^2})\)

Diện tích hình chữ nhật \(ABCD\) là: \({S_{ABC{\rm{D}}}} = 5{\rm{x}}\left( {c{m^2}} \right)\)

Theo đề bài ta có: 

\(\begin{array}{l}
{S_{ABC{\rm{D}}}} = 3{S_{ADE}} \\\Rightarrow 5{\rm{x}} = 3.5 = 15\\
\Rightarrow x = 15:5 = 3cm.
\end{array}\) 

Vậy \(x = 3cm.\)

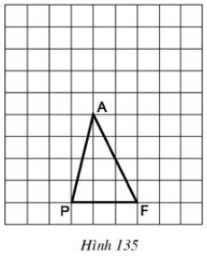
Tam giác \(PAF\) được vẽ trên giấy kẻ ô vuông (h.\(135\)).

Hãy chỉ ra:

a) Một điểm \(I\) sao cho \({S_{PIF}} = {S_{PAF}}\)

b) Một điểm \(O\) sao cho \({S_{POF}} = 2.{S_{PAF}}\)

c) Một điểm \(N\) sao cho \({S_{PNF}} = \dfrac{1}{2}{S_{PAF}}\)

Phương pháp giải

Áp dụng

- Cách tính diện tích tam giác.

- Khoảng cách giữa hai đường thẳng song song.

Hướng dẫn giải

a) Nếu lấy điểm \(I\) bất kì nằm trên đường thẳng \(d\) đi qua \(A\) và song song với đường thẳng \(PF\) thì \({S_{PIF}} = {S_{PAF}}\)

(vì khi đó hai tam giác chung đáy \(PF\) và chiều cao hạ từ \(A\) hay \(I\) xuống \(PF\) đều bằng nhau (\(d // PF\)))

Có vô số điểm \(I\) thỏa mãn yêu cầu bài toán nằm trên đường thẳng \(d\) song song với \(PF\).

b) Nếu lấy một điểm \(O\) sao cho khoảng cách từ \(O\) đến đường thẳng \(PF\) bằng hai lần khoảng cách từ \(A\) đến đường thẳng \(PF\) thì \({S_{POF}} = 2.{S_{PAF}}\)

(vì khi đó hai tam giác chung đáy \(PF\) và chiều cao hạ từ \(O\) xuống \(PF\) bằng \(2\) lần chiều cao hạ từ \(A\) xuống \(PF\))

Có vô số điểm \(O\) thỏa mãn yêu cầu bài toán nằm trên đường thẳng \(f\) song song với \(PF\).

c) Nếu lấy điểm \(N\) sao cho khoảng cách từ \(N\) đến đường thẳng \(PF\) bằng \(\dfrac{1}{2}\) khoảng cách từ \(A\) đến \(PF\) thì \({S_{PNF}} = \dfrac{1}{2}{S_{PAF}}\)

(vì khi đó hai tam giác chung đáy \(PF\) và chiều cao hạ từ \(N\) xuống \(PF\) bằng \(\dfrac{1}{2}\) chiều cao hạ từ \(A\) xuống \(PF\))

Có vô số điểm \(N\) như thế nằm trên đường thẳng \(g\) song song với \(PF.\)

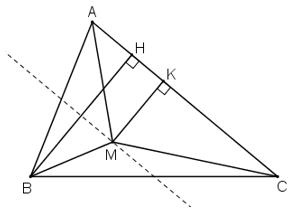
Cho tam giác \(ABC\). Hãy chỉ ra một số vị trí của điểm \(M\) nằm trong tam giác đó sao cho:

\({S_{AMB}} + {S_{BMC}} = {S_{MAC}}\)

Phương pháp giải

- Kẻ đường cao \(BH, MK.\)

- Áp dụng công thức tính diện tích tam giác: Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

Hướng dẫn giải

Kẻ đường cao \(BH, MK.\)  

Theo giả thiết, \(M\) là điểm nằm trong tam giác \(ABC\) sao cho:

\({S_{AMB}} + {\rm{ }}{S_{BMC}} = {\rm{ }}{S_{MAC}}\)  (1)

Ta lại có: \({S_{AMB}} + {S_{BMC}} + {S_{MAC}} = {S_{ABC}}\)    (2)

Thay (1) vào (2) ta được: \({S_{MAC}}+ {S_{MAC}}={S_{ABC}}\)

\(\Rightarrow 2.{S_{MAC}} = {S_{ABC}}\)

\(\Rightarrow {S_{MAC}} = \dfrac{1}{2}{S_{ABC}}\)

\(\Rightarrow \dfrac{1}{2}MK.AC = \dfrac{1}{2}\left( {\dfrac{1}{2}BH.AC} \right)\)

\(⇒MK = \dfrac{1}{2}BH\)

Do đó, \(M\) nằm trên đường thẳng thuộc nửa mặt phẳng bờ \(AC\) chứa \(B\) sao cho khoảng cách từ \(M\) đến \(AC\) bằng \(\dfrac{1}{2}\) đường cao \(BH\).

Vậy điểm \(M\) nằm trong tam giác \(ABC\) và nằm trên đường trung bình ứng với cạnh \(AC\) của \(ΔABC\)

Tính diện tích tam giác cân có cạnh đáy bằng \(a\) và cạnh bên bằng \(b.\)

Phương pháp giải

- Tam giác cân là tam giác có hai cạnh bằng nhau.

- Định lí Pytago: Bình phương cạnh huyền bằng tổng cách bình phương của hai cạnh góc vuông.

- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.

Hướng dẫn giải

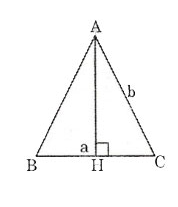
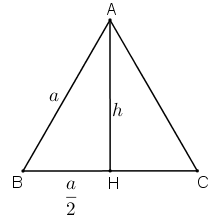
Gọi \(h\) là chiều cao của tam giác cân có đáy là \(a\) và cạnh bên là \(b.\) 

Xét tam giác \(ABC\) cân tại \(A\) có \(AB=b, BC=a\) và chiều cao \(AH=h\). Ta tính diện tích tam giác \(ABC\).

Vì \(\Delta ABC\) cân tại \(A\) (gt) nên \(AH\) vừa là đường cao vừa là đường trung tuyến (tính chất tam giác cân). Suy ra, \(H\) là trung điểm của \(BC\).

\( \Rightarrow BH = \dfrac{{BC}}{2} = \dfrac{a}{2}\)

Áp dụng định lý Pitago vào tam giác vuông \(ABH\) ta có: 

\(A{H^2} = A{B^2} - B{H^2}\)

\({h^2} = {b^2} - {\left( {\dfrac{a}{2}} \right)^2} = \dfrac{{4{b^2} - {a^2}}}{4} \)\(\Rightarrow h = \dfrac{{\sqrt {4{b^2} - {a^2}} }}{2}\)

Diện tích tam giác \(ABC\) là: 

\(S = \dfrac{1}{2}ah = \dfrac{1}{2}a.\dfrac{{\sqrt {4{b^2} - {a^2}} }}{2} \)\(= \dfrac{1}{4}a\sqrt {4{b^2} - {a^2}} .\)

Tính diện tích của một tam giác đều có cạnh là \(a.\)

Phương pháp giải