Giải bài tập SGK Toán 8 Bài 3: Phương trình đưa được về dạng ax + b = 0
Phần hướng dẫn giải bài tập Toán 8 Chương 3 Bài 3 Phương trình đưa được về dạng ax + b = 0 sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng, giải bài tập từ SGK Đại số 8 Tập 2
Mục lục nội dung
1. Giải bài 10 trang 12 SGK Toán 8 tập 2
2. Giải bài 11 trang 13 SGK Toán 8 tập 2
3. Giải bài 12 trang 13 SGK Toán 8 tập 2
4. Giải bài 13 trang 13 SGK Toán 8 tập 2
5. Giải bài 14 trang 13 SGK Toán 8 tập 2
6. Giải bài 15 trang 13 SGK Toán 8 tập 2
7. Giải bài 16 trang 13 SGK Toán 8 tập 2
8. Giải bài 17 trang 14 SGK Toán 8 tập 2
9. Giải bài 18 trang 14 SGK Toán 8 tập 2

1. Giải bài 10 trang 12 SGK Toán 8 tập 2
Tìm chỗ sai và sửa lại các bài giải sau cho đúng:
a) \(3x - 6 + x = 9 - x\)
\(\Leftrightarrow 3x + x - x = 9 - 6\)
\(\Leftrightarrow 3x = 3\)
\(\Leftrightarrow x = 1\)
b) \(2t - 3 + 5t = 4t + 12\)
\(\Leftrightarrow 2t + 5t - 4t = 12 -3\)
\(\Leftrightarrow 3t = 9\)
\(\Leftrightarrow t = 3.\)
Phương pháp giải
Áp dụng qui tắc chuyển vế: Trong một phương trình, ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.
Hướng dẫn giải
Câu a
Sai ở phương trình thứ hai chuyển vế hạng tử \(-6\) từ vế trái sang vế phải, hạng tử \(-x\) từ vế phải sang vế trái mà không đổi dấu.
Giải lại:
\(3x - 6 + x = 9 - x\)
\( \Leftrightarrow 3x + x + x = 9 + 6\)
\( \Leftrightarrow 5x = 15\)
\( \Leftrightarrow x = 15 : 5\)
\( \Leftrightarrow x = 3\)
Vậy phương trình có nghiệm duy nhất \(x = 3\)
Câu b
Sai ở phương trình thứ hai, chuyển vế hạng tử \(-3\) từ vế trái sang vế phải mà không đổi dấu.
Giải lại:
\(2t - 3 + 5t = 4t + 12\)
\( \Leftrightarrow 2t + 5t - 4t = 12 + 3\)
\( \Leftrightarrow 3t = 15\)
\( \Leftrightarrow t = 15 : 3\)
\( \Leftrightarrow t = 5\)
Vậy phương trình có nghiệm duy nhất \(t = 5\).
2. Giải bài 11 trang 13 SGK Toán 8 tập 2
Giải các phương trình:
a) \(3x - 2 = 2x - 3\)
b) \(3 - 4u + 24 + 6u = u + 27 + 3u\)
c) \(5 - (x - 6) = 4(3 - 2x)\)
d) \(-6(1,5 - 2x) = 3(-15 + 2x)\)
e) \(0,1 - 2(0,5t - 0,1) = 2(t - 2,5) - 0,7\)
f) \(\frac{3}{2}(x -\frac{5}{4})-\frac{5}{8}= x\)
Phương pháp giải
a+b) Thực hiện quy tắc chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).
c+d+e) Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).
f) Thực hiện các bước sau:
+ Quy đồng mẫu hai vế và khử mẫu.
+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).
Hướng dẫn giải
Câu a: \(3x - 2 = 2x - 3\)
\(⇔ 3x - 2x = -3 + 2\)
\(⇔ x = -1\)
Vậy phương trình có nghiệm duy nhất \(x = -1.\)
Câu b: \(3 - 4u + 24 + 6u = u + 27 + 3u\)
\(⇔ 2u + 27 = 4u + 27\)
\(⇔ 2u - 4u = 27 - 27\)
\(⇔ -2u = 0\)
\(⇔ u = 0\)
Vậy phương trình có nghiệm duy nhất \(u = 0.\)
Câu c: \(5 - (x - 6) = 4(3 - 2x)\)
\(⇔ 5 - x + 6 = 12 - 8x\)
\(⇔ -x + 11 = 12 - 8x\)
\(⇔ -x + 8x = 12 - 11\)
\(⇔ 7x = 1\)
\(⇔ x= \dfrac{1}{7}\)
Vậy phương trình có nghiệm duy nhất \(x = \dfrac{1}{7}\).
Câu d: \(-6(1,5 - 2x) = 3(-15 + 2x)\)
\(⇔ -9 + 12x = -45 + 6x\)
\(⇔ 12x - 6x = -45 + 9\)
\(⇔ 6x = -36\)
\(⇔ x = -36:6\)
\(⇔ x = -6\)
Vậy phương trình có nghiệm duy nhất \(x = -6\).
Câu e: \(0,1 - 2(0,5t - 0,1) = 2(t - 2,5)\)\(\, - 0,7\)
\(⇔ 0,1 - t + 0,2 = 2t - 5 - 0,7\)
\(⇔ -t + 0,3= 2t - 5,7\)
\(⇔ -t - 2t = -5,7 - 0,3\)
\(⇔ -3t = -6\)
\(⇔ t = (-6):(-3)\)
\(⇔ t = 2\)
Vậy phương trình có nghiệm duy nhất \(t = 2\)
Câu f: \( \dfrac{3}{2}(x -\dfrac{5}{4})-\dfrac{5}{8} = x\)
\(⇔ \dfrac{3}{2}x - \dfrac{15}{8} - \dfrac{5}{8} = x\)
\(⇔ \dfrac{3}{2}x -x=\dfrac{15}{8}+\dfrac{5}{8}\)
\(⇔ \dfrac{1}{2}x = \dfrac{20}{8}\)
\(⇔ x = \dfrac{20}{8} : \dfrac{1}{2}\)
\(⇔ x = 5\)
Vậy phương trình có nghiệm duy nhất \(x = 5\).
3. Giải bài 12 trang 13 SGK Toán 8 tập 2
Giải các phương trình:
a) \(\frac{5x-2}{3}=\frac{5-3x}{2}\)
b) \(\frac{10x+3}{12}=1+\frac{6+8x}{9}\)
c) \(\frac{7x-1}{6}+ 2x =\frac{16 - x}{5}\)
d) \(4(0,5 - 1,5x) =-\frac{5x-6}{3}\)
Phương pháp giải
- Để giải các phương trình đưa được về \(ax + b = 0\) ta thường biến đổi phương trình như sau:
+ Quy đồng mẫu hai vế phương trình và khử mẫu.
+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).
+ Tìm nghiệm của phương trình dạng \(ax+b=0\)
Hướng dẫn giải
Câu a
\( \dfrac{5x-2}{3}=\dfrac{5-3x}{2}\)
\( \Leftrightarrow \dfrac{{2\left( {5x - 2} \right)}}{6} = \dfrac{{3\left( {5 - 3x} \right)}}{6}\)
\(⇔ 2(5x - 2) = 3(5 - 3x)\)
\(⇔ 10x - 4 = 15 - 9x\)
\(⇔ 10x + 9x = 15 + 4\)
\(⇔ 19x = 19\)
\( \Leftrightarrow x = 19:19\)
\(⇔ x = 1\)
Vậy phương trình có nghiệm duy nhất \(x = 1\).
Câu b
\( \dfrac{10x+3}{12}=1+\dfrac{6+8x}{9}\)
\(⇔ \dfrac{3(10x+3)}{36}=\dfrac{{36}}{{36}} + \dfrac{{4(6 + 8x)}}{{36}}\)
\(⇔ 30x + 9 = 36 + 24 + 32x\)
\(⇔ 30x - 32x = 60 - 9\)
\(⇔ -2x = 51\)
\(⇔ x = \dfrac{-51}{2}\)
\(\Leftrightarrow x= -25,5\)
Vậy phương trình có nghiệm duy nhất \(x = -25,5\).
Câu c
\( \dfrac{7x-1}{6} + 2x = \dfrac{16 - x}{5}\)
\( \Leftrightarrow \dfrac{{5.\left( {7x - 1} \right)}}{{30}} + \dfrac{{30.2x}}{{30}} = \dfrac{{6.\left( {16 - x} \right)}}{{30}}\)
\( \Leftrightarrow 5.\left( {7x - 1} \right) + 60x = 6\left( {16 - x} \right)\)
\( \Leftrightarrow 35x - 5 + 60x = 96 - 6x\)
\(⇔ 95x -5 = 96 - 6x\)
\(⇔ 95x + 6x = 96 + 5\)
\(⇔ 101x = 101\)
\( \Leftrightarrow x = 101:101\)
\(⇔ x = 1\)
Vậy phương trình có nghiệm duy nhất \(x = 1\).
Câu d
\(4(0,5 - 1,5x) = -\dfrac{5x-6}{3}\)
\(⇔ 2 - 6x = -\dfrac{5x-6}{3}\)
\( \Leftrightarrow \dfrac{{3\left( {2 - 6x} \right)}}{3} = - \dfrac{{5x - 6}}{3}\)
\(⇔ 3(2 - 6x)= - (5x-6)\)
\( ⇔ 6 - 18x = -5x + 6\)
\( ⇔ -18x + 5x = 6-6\)
\( ⇔ -13x = 0\)
\( \Leftrightarrow x = 0:( - 13)\)
\( ⇔ x = 0\)
Vậy phương trình có nghiệm duy nhất \(x = 0.\)
4. Giải bài 13 trang 13 SGK Toán 8 tập 2
Bạn Hoà giải phương trình \(x(x + 2) = x(x + 3)\) như hình 2.
Theo em bạn Hoà giải đúng hay sai?
Em sẽ giải phương trình đó như thế nào?
Phương pháp giải
Quy tắc chuyển vế
Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.
Quy tắc nhân với một số:
Trong một phương trình, ta có thể nhân (hoặc chia) cả hai vế với cùng một số khác \(0\).
Hướng dẫn giải
Bạn Hoà đã giải sai.
Không thể chia hai vế của phương trình đã cho với \(x\) để được phương trình \(x + 2 = x + 3\) (vì ta chưa biết \(x\) có khác 0 hay không)
Lời giải đúng:
\(\eqalign{
& x\left( {x + 2} \right) = x\left( {x + 3} \right) \cr
& \Leftrightarrow {x^2} + 2x = {x^2} + 3x \cr
& \Leftrightarrow {x^2} + 2x - {x^2} - 3x = 0 \cr
& \Leftrightarrow - x = 0 \cr
& \Leftrightarrow x = 0 \cr} \)
Vậy phương trình đã cho có nghiệm là \(x = 0\).
5. Giải bài 14 trang 13 SGK Toán 8 tập 2
Số nào trong ba số \(-1; 2\) và \(-3 \) nghiệm đúng mỗi phương trình sau:
\(\left| x \right| = x\;\;\;\;\;\;\;\left( 1 \right)\)
\({x^2} + 5x + 6 = 0\;\;\;\;\;\;\left( 2 \right)\)
\(\dfrac{6}{{1 - x}} = x + 4\;\;\;\;\;\;\;\;\left( 3 \right)\)
Phương pháp giải
Thay các giá trị vào hai vế của từng phương trình, nếu kết quả vế trái bằng vế phải thì đó là nghiệm của phương trình.
Hướng dẫn giải
*) Xét phương trình: \(|x|=x\;\;\;\;\;(1)\)
- Thay \(x=-1\) và hai vế của phương trình (1) ta được:
\(\left. \matrix{
VT = | - 1| = 1 \hfill \cr
VP = - 1 \hfill \cr} \right\} \Rightarrow VT \ne VP\)
Vậy \(x=-1\) không là nghiệm của phương trình (1).
- Thay \(x=2\) và hai vế của phương trình (1) ta được:
\(\left. \matrix{
VT = |2| = 2 \hfill \cr
VP = 2 \hfill \cr} \right\} \Rightarrow VT = VP\)
Vậy \(x=2\) là nghiệm của phương trình (1).
- Thay \(x= -3\) và hai vế của phương trình (1) ta được:
\(\left. \matrix{
VT = | - 3| = 3 \hfill \cr
VP = - 3 \hfill \cr} \right\} \Rightarrow VT \ne VP\)
Vậy \(x=-3\) không là nghiệm của phương trình (1).
*) Xét phương trình \({x^2} + 5x + 6 = 0\;\;\;\;\;\;\left( 2 \right)\)
- Thay \(x=-1\) vào hai vế của phương trình (2) ta được:
\(\left. \matrix{
VT = {\left( { - 1} \right)^2} + 5.\left( { - 1} \right) + 6 = 2 \hfill \cr
VP = 0 \hfill \cr} \right\} \)\(\,\Rightarrow VT \ne VP\)
Vậy \(x=-1\) không là nghiệm của phương trình (2).
- Thay \(x=2\) vào hai vế của phương trình (2) ta được:
\(\left. \matrix{
VT = {2^2} + 5.2 + 6 = 20 \hfill \cr
VP = 0 \hfill \cr} \right\}\)\(\, \Rightarrow VT \ne VP\)
Vậy \(x=2\) không là nghiệm của phương trình (2).
- Thay \(x=-3\) vào hai vế của phương trình (2) ta được:
\(\left. \matrix{
VT = {\left( { - 3} \right)^2} + 5.\left( { - 3} \right) + 6 = 0 \hfill \cr
VP = 0 \hfill \cr} \right\}\)\(\, \Rightarrow VT = VP\)
Vậy \(x=-3\) là nghiệm của phương trình (2).
*) Xét \(\dfrac{6}{{1 - x}} = x + 4\;\;\;\;\;\;\;\;\left( 3 \right)\)
- Thay \(x=-1\) vào hai vế của phương trình (3) ta được:
\(\left. \matrix{
VT =\dfrac{6}{{1 - ( - 1)}} = \dfrac{6}{2} = 3 \hfill \cr
VP = ( - 1) + 4 = 3 \hfill \cr} \right\} \)\(\,\Rightarrow VT = VP\)
Vậy \(x=-1\) là nghiệm của phương trình (3)
- Thay \(x=2\) vào hai vế của phương trình (3) ta được:
\(\left. \matrix{
VT =\dfrac{6}{{1 - 2}} = \dfrac{6}{{ - 1}} = - 6 \hfill \cr
VP = 2 + 4 = 6 \hfill \cr} \right\}\)\(\, \Rightarrow VT \ne VP\)
Vậy \(x=2\) không là nghiệm của phương trình (3).
- Thay \(x=-3\) vào hai vế của phương trình (3) ta được:
\(\left. \matrix{
VT = \dfrac{6}{{1 - ( - 3)}} = \dfrac{6}{4} = \dfrac{3}{2} \hfill \cr
VP = ( - 3) + 4 = 1 \hfill \cr} \right\}\)\(\, \Rightarrow VT \ne VP\)
Vậy \(x=-3\) không là nghiệm của phương trình (3).
(Với VT là vế trái, VP là vế phải)
6. Giải bài 15 trang 13 SGK Toán 8 tập 2
Một xe máy khởi hành từ Hà Nội đi Hải Phòng với vận tốc trung bình \(32\) km/h. Sau đó \(1\) giờ, một ô tô cũng khởi hành từ Hà Nội đi Hải Phòng, cùng đường với xe máy và với vận tốc trung bình \(48\) km/h. Hãy viết phương trình biểu thị việc ô tô gặp xe máy sau x giờ, kể từ khi ô tô khởi hành.
Phương pháp giải
Áp dụng công thức: \(S=vt\)
Trong đó: \(S\) là quãng đường đi được trong thời gian \(t\),
\(v\) là vận tốc,
\(t\) là thời gian.
Hướng dẫn giải
Gọi x là thời gian chuyển động của ô tô kể từ thời điểm xuất phát đến lúc hai xe gặp nhau. (\(x > 0\); giờ)
Quãng đường của ô tô đi trong \(x\) giờ là: \(48x\) (km)
Vì xe máy khởi hành trước ô tô là \(1\) giờ nên thời gian xe máy đi tính từ lúc khởi hành cho đến lúc hai xe gặp nhau là: \(x+1\) (giờ)
Quãng đường của xe máy đi được khi ô tô chuyển động được \(x\) giờ là: \(32(x+1)\) (km)
Vì hai xe đi cùng một quãng đường nên ta có phương trình: \(48x = 32(x+1)\)
Vậy phương trình biểu thị việc ô tô gặp xe máy sau \(x\) giờ, kể từ khi ô tô khởi hành là: \(48x = 32(x+1)\)
7. Giải bài 16 trang 13 SGK Toán 8 tập 2
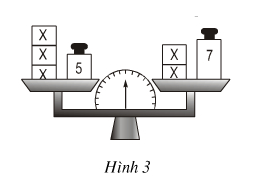
Viết phương trình biểu thị cân thăng bằng trong hình 3 (đơn vị khối lượng là gam).
Phương pháp giải
- Biểu thị theo x khối lượng mỗi bên của cân.
- Vì cân thăng bằng nên khối lượng bên vế trái = vế phải. Do đó, ta có phương trình cần tìm.
Hướng dẫn giải
Khối lượng ở đĩa cân bên trái là \(3x + 5\) (gam)
Khối lượng ở đĩa cân bên phải là \(2x + 7\) (gam)
Vì hai đĩa cân thăng bằng nên ta có phương trình: \(3x + 5 = 2x + 7\)
8. Giải bài 17 trang 14 SGK Toán 8 tập 2
Giải các phương trình:
a) \(7 + 2x = 22 - 3x\)
b) \(8x - 3 = 5x + 12\)
c) \(x - 12 + 4x = 25 + 2x - 1\)
d) \(x + 2x + 3x - 19 = 3x + 5;\)
e) \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
f) (\left( {x - 1} \right) - \left( {2x - 1} \right) = 9 - x\)
Phương pháp giải
Qui tắc chuyển vế:
Trong một phương trình ta có thể chuyển một hạng tử từ vế này sang vế kia và đổi dấu hạng tử đó.
Từ đó đưa về phương trình bậc nhất 1 ẩn để giải.
Hướng dẫn giải
Câu a: \(7 + 2x = 22 - 3x\)
⇔ \(2x + 3x = 22 - 7\)
⇔ \(5x = 15\)
⇔ \(x = 15:5\)
⇔ \(x = 3\)
Vậy phương trình có nghiệm \(x = 3\).
Câu b: \(8x - 3 = 5x + 12\)
⇔ \(8x - 5x = 12 +3\)
⇔ \(3x = 15\)
⇔ \(x = 15:3\)
⇔ \(x = 5\)
Vậy phương trình có nghiệm \(x = 5\).
Câu c: \(x - 12 + 4x = 25 + 2x - 1\)
⇔ \(5x - 12 = 2x + 24\)
⇔ \(5x - 2x = 24 + 12\)
⇔ \(3x = 36\)
⇔ \(x = 36:3\)
⇔ \(x = 12\)
Vậy phương trình có nghiệm \(x = 12\).
Câu d: \(x + 2x + 3x - 19 = 3x + 5\)
⇔ \(6x - 19 = 3x+5\)
⇔ \(6x - 3x = 5 + 19\)
⇔ \(3x= 24\)
⇔ \(x= 24 : 3\)
⇔ \(x= 8\)
Vậy phương trình có nghiệm \(x = 8\).
Câu e: \(7 - \left( {2x + 4} \right) = - \left( {x + 4} \right)\)
⇔ \(7 - 2x - 4 = -x - 4\)
⇔\(-2x + x = - 4-7 + 4\)
⇔ \(-x = - 7\)
⇔ \(x=(-7):(-1)\)
⇔ \(x = 7\)
Vậy phương trình có nghiệm \(x = 7\).
Câu f: \(\left( {x - 1} \right) - \left( {2x - 1} \right) = 9 - x\)
⇔ \(x - 1 - 2x + 1 = 9 - x\)
⇔ \(-x=9-x\)
⇔ \(-x +x = 9\)
⇔ \(0x = 9\) (vô lý)
Phương trình vô nghiệm.
9. Giải bài 18 trang 14 SGK Toán 8 tập 2
Giải các phương trình:
a) \(\dfrac{x}{3} - \dfrac{{2x + 1}}{2} = \dfrac{x}{6} - x\)
b) \(\dfrac{{2 + x}}{5} - 0,5x = \dfrac{{1 - 2x}}{4} + 0,25\)
Phương pháp giải
Các bước thực hiện giải phương trình đưa về dạng \(ax+b=0\)
+ Quy đồng mẫu hai vế và khử mẫu.
+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).
+ Tìm nghiệm của phương trình dạng \(ax+b=0\)
Hướng dẫn giải
Câu a
\(\eqalign{
& {x \over 3} - {{2x + 1} \over 2} = {x \over 6} - x \cr
& \Leftrightarrow {{2x} \over 6} - {{3.\left( {2x + 1} \right)} \over 6} = {x \over 6} - {{6x} \over 6} \cr
& \Leftrightarrow 2x-3\left( {2x + 1} \right) = x-6x \cr
& \matrix{
{ \Leftrightarrow 2x - 6x-3 = - 5x} \hfill \cr
{ \Leftrightarrow - 4x + 5x = 3} \hfill \cr
{ \Leftrightarrow x = 3} \hfill \cr} \cr} \)
Phương trình có nghiệm \(x = 3\).
Câu b
\(\eqalign{& {{2 + x} \over 5} - 0,5x = {{1 - 2x} \over 4} + 0,25 \cr
& \Leftrightarrow {{2 + x} \over 5} - {1 \over 2}x = {{1 - 2x} \over 4} + {{25} \over {100}} \cr
& \Leftrightarrow {{4\left( {2 + x} \right)} \over {20}} - {{10x} \over {20}} = {{5\left( {1 - 2x} \right)} \over {20}} + {5 \over {20}} \cr & \Leftrightarrow 4\left( {2 + x} \right)-10x = 5\left( {1-2x} \right) + 5 \cr
& \matrix{{ \Leftrightarrow 8 + 4x-10x = 5-10x + 5} \hfill \cr
{ \Leftrightarrow 4x-10x+10x = 5+5-8} \hfill \cr
{ \Leftrightarrow 4x = 10 - 8} \hfill \cr
\matrix{\Leftrightarrow 4x = 2 \hfill \cr
\Leftrightarrow x =\dfrac{2}{4} \hfill \cr} \hfill \cr} \cr & \Leftrightarrow x = {1 \over 2} \cr} \)
Vậy phương trình có nghiệm \(x = \dfrac{1 }{ 2}\)
10. Giải bài 19 trang 14 SGK Toán 8 tập 2
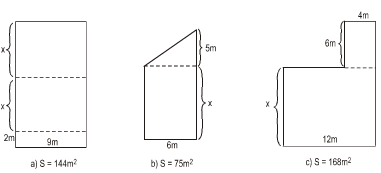
Viết phương trình ẩn x rồi tính x (mét), trong mỗi hình dưới đây (h.4) (S là diện tích của hình):
Phương pháp giải
Công thức tính diện tích hình chữ nhật: \(S=a\times b\)
Trong đó: \(S\) là diện tích hình chữ nhật
\(a\) là chiều dài hình chữ nhật
\(b\) là chiều rộng hình chữ nhật
Công thức tính diện tích hình thang: \(S = \dfrac{{h\left( {a + b} \right)}}{2}\)
Trong đó: \(S\) là diện tích hình thang
\(a\) và \(b\) là độ dài hai đáy của hình thang
\(h\) là chiều cao của hình thang.
- Để giải các phương trình đưa được về \(ax + b = 0\) ta thường biến đổi phương trình như sau:
+ Quy đồng mẫu hai vế và khử mẫu.
+ Thực hiện phép tính để bỏ dấu ngoặc và chuyển vế các hạng tử để đưa phương trình về dạng \(ax + b=0\) hoặc \(ax=-b\).
+ Tìm \(x\)
Hướng dẫn giải
Câu a: Diện tích hình chữ nhật là \(S = 9(2x + 2)(m^2)\).
Vì diện tích \(S = 144\) m2 nên ta có phương trình:
\(9(2x +2) = 144\)
\(⇔18 x + 18 = 144\)
\(⇔18 x = 144 - 18\)
\(⇔18x = 126\)
\(\Leftrightarrow x=126:18\)
\(⇔ x = 7\)
Vậy \(x = 7\,m\)
Câu b: Đáy nhỏ của hình thang là: \(x(m)\)
Đáy lớn của hình thang là: \(x + 5(m)\)
Diện tích hình thang là: \(S = \dfrac{1}{2}.6.\left( {x + x + 5} \right) = 3.\left( {2x + 5} \right)\) \((m^2)\)
Mà \(S = 75\left( {{m^2}} \right)\) nên ta có phương trình:
\(3(2x + 5) = 75\)
\( \Leftrightarrow 2x + 5 = 75:3\)
\(⇔2x + 5 = 25\)
\( \Leftrightarrow 2x = 25 - 5\)
\(⇔2x = 20\)
\( \Leftrightarrow x = 20:2\)
\(⇔x = 10\)
Vậy \(x = 10\;m\).
Câu c: Biểu thức tính diện tích hình là:
\(S = 12.x + 6.4 = 12x + 24\) \((m^2)\)
Mà \(S = 168\) m2 nên ta có:
\(12x + 24 = 168\)
\( \Leftrightarrow 12x = 168 - 24\)
\( \Leftrightarrow 12x = 144\)
\( \Leftrightarrow x = 144:12\)
\(\Leftrightarrow x = 12\)
Vậy \(x = 12\,m.\)
11. Giải bài 20 trang 14 SGK Toán 8 tập 2
Đố: Trung bảo Nghĩa hãy nghĩ ở trong đầu một số tự nhiên tùy ý, sau đó Nghĩa thêm \(5\) vào số ấy, nhân tổng nhận được với \(2\), được bao nhiêu đem trừ đi \(10\), tiếp tục nhân hiệu tìm được với \(3\) rồi cộng thêm \(66\), cuối cùng chia kết quả cho \(6\). Chẳng hạn, nếu Nghĩa nghĩ đến số \(7\) thì quá trình tính toán sẽ là: \(7 → (7 + 5= 12) →(12\times 2=24)\) \(→(24 - 10 = 14) → (14 \times 3 = 42)\) \(→ (42 + 66 = 108) → (108 : 6 = 18)\)
Trung chỉ cần biết kết quả cuối cùng (số \(18\)) là đoán ngay được số Nghĩa đã nghĩ là số nào.
Nghĩa thử mấy lần, Trung đều đoán đúng. Nghĩa phục tài Trung lắm. Đố em tìm ra bí quyết của Trung đấy!
Phương pháp giải
Lập phương trình biểu diễn mối quan hệ giữa số mà Nghĩa nghĩ và kết quả cuối cùng.
Hướng dẫn giải
+ Bí quyết của Trung lấy kết quả cuối cùng của Nghĩa trừ đi 11 thì được số của Nghĩa nghĩ ra lúc đầu.
+ Thật vậy:
- Gọi \(x\) là số mà Nghĩa nghĩ. Theo đề bài số cuối cùng của Nghĩa đọc ra là:
\(\dfrac{{\left[ {\left( {x + 5} \right).2 - 10} \right].3 + 66}}{6}\)
- Gọi \(X\) là số cuối cùng ta có phương trình:
\(⇔\dfrac{{\left[ {\left( {x + 5} \right).2 - 10} \right].3 + 66}}{6} = X\)
\(⇔\dfrac{{\left[ {2x + 10 - 10} \right].3 + 66}}{6} = X\)
\(⇔\dfrac{{6x + 66}}{6} = X\)
\( \Leftrightarrow \dfrac{{6(x + 11)}}{6} = X\)
\(⇔ x + 11 = X\)
\(⇔ x = X – 11\).
Vậy Trung chỉ cần lấy số cuối cùng của Nghĩa đọc trừ đi \(11\) thì được số của Nghĩa đã nghĩ ra.
Tham khảo thêm
- doc Giải bài tập SGK Toán 8 Bài 1: Mở đầu về phương trình
- doc Giải bài tập SGK Toán 8 Bài 2: Phương trình bậc nhất một ẩn và cách giải
- doc Giải bài tập SGK Toán 8 Bài 4: Phương trình tích
- doc Giải bài tập SGK Toán 8 Bài 5: Phương trình chứa ẩn ở mẫu
- doc Giải bài tập SGK Toán 8 Bài 6: Giải bài toán bằng cách lập phương trình
- doc Giải bài tập SGK Toán 8 Bài 7: Giải bài toán bằng cách lập phương trình (tiếp theo)
- doc Giải bài tập SGK Toán 8 Ôn tập chương 3: Phương trình bậc nhất một ẩn