Giải bài tập SGK Toán 8 Bài 8: Diện tích xung quanh của hình chóp đều

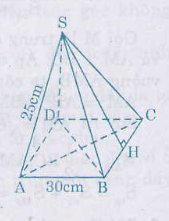
Một hình chóp tứ giác đều có độ dài cạnh bên bằng \(25cm\), đáy là hình vuông \(ABCD\) cạnh \(30cm\).

Tính diện tích toàn phần của hình chóp.

Phương pháp giải

- Tính diện tích xung quanh: \(S_{xq}= p.d \), trong đó \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều. 

- Tính diện tích đáy theo công thức diện tích hình vuông: \(S_{hv}\) = cạnh \(\times \) cạnh.

- Tính diện tích toàn phần: \(S_{tp}= S_{xq} + S_{đ}\)

Hướng dẫn giải

Gọi \(H\) là trung điểm của \(BC\). 

Khi đó ta có: \(BH = HC = \dfrac{1}{2}BC =\dfrac{1}{2}. 30=15 \,cm  \)

Vì tam giác \(SBC\) cân tại \(S\) nên \( SH\perp BC \).

Ta có:  \(d = SH = \sqrt{SB^2- BH^2}\) \( = \sqrt{25^2 -15^2} = \sqrt{400}=20(cm)\) 

Chu vi đáy là: \(4. 30 = 120 (cm)\)

Diện tích xung quanh của hình chóp:

\(S_{xq} = p.d =\dfrac{1}{2} .120.20 = 1200 (cm^2) \) 

Diện tích đáy là:  

\( S_{đ} = 30.30 = 900 (cm^2)\)

Diện tích toàn phần của hình chóp là:

\( S_{tp} =S_{xq}+ S_{đ} = 1200 + 900 \) \(= 2100 (cm^2) \)

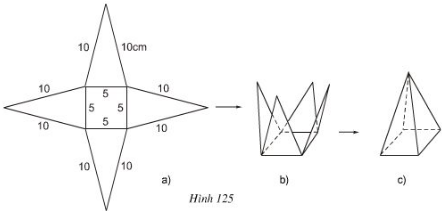
Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.

a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?

b) Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.

c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?

Phương pháp giải

- Diện tích xung quanh của hình chóp đều bằng tích của nửa chu vi đáy với trung đoạn: Sxq = p.d.

- Diện tích toàn phần bằng tổng của diện tích xung quanh và diện tích đáy.

Hướng dẫn giải

a) Trong hình 125a có 4 tam giác cân bằng nhau.

b) 

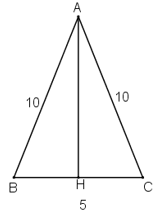
Gọi H là chân đường cao hạ từ A xuống BC, mà tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến. 

Do đó \(HC=BC:2=\dfrac{5}{2}cm\)

Xét tam giác AHC vuông tại H, theo định lý Py-ta-go ta có:

 \(AH = \sqrt{AC^{2}- HC^{2}}\)

 \(= \sqrt{10^{2}- {\left( {\dfrac{5}{2}} \right)^2}} = \sqrt{100-\dfrac{25}{4}} \)

 \(\approx  9,68\) \(cm\)  

c) Chu vi đáy của hình chóp là \(4.5 = 20 (cm).\) 

Diện tích xung quanh hình chóp:

\(S_{xq} = p. d =\dfrac{1}{2}.20.9,68 = 96,8\) \( (cm^2) \) 

Diện tích đáy:

\( S_{đ} = 5^2 = 25 (cm^2) \) 

Diện tích toàn phần của hình chóp:

\( S_ {tp} = S_{xq}+ S_{đ} = 96,8 + 25 = 121,8\) \((cm^2) \)

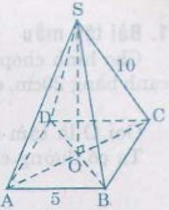
Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên hình 125.

Phương pháp giải

Chân đường cao của hình chóp đều là tâm của đường tròn đi qua các đỉnh của mặt đáy.

Và áp dụng định lý Pytago trong tam giác vuông.

Hướng dẫn giải

Gọi tên như hình vẽ.

Gọi \(O\) là giao điểm hai đường chéo của hình vuông đáy. Khi đó SO là chiều cao của hình chóp tứ giác đều. Ta đi tính SO.

Tam giác \(ABC\) vuông tại \(B\) nên theo định lý Pytago, ta có :  

\( AC^2 = AB^2 + BC^2 \)\(\,= 5^2 + 5^2 = 50 \) 

Vì ABCD là hình vuông nên O là trung điểm của AC. Suy ra \(OC=\dfrac{AC}{2}\)

Tam giác \(SOC\) vuông tại \(O\) nên the định lý Pytago, ta có: 

\( SO^2 + OC^2 = SC^2\)

\( \Rightarrow SO^2 = SC^2 - OC^2 \)\(\,=  SC^2 - {\left( {\dfrac{{AC}}{2}} \right)^2}\) 

\( SO =  \sqrt{SC^{2}- {\left( {\dfrac{{AC}}{2}} \right)^2}}\)\(\,= \sqrt{10^{2}- \dfrac{50}{4}}\) \(\approx 9,35\, (cm)\)

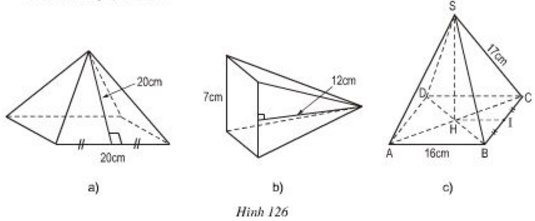
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (h.126).

Phương pháp giải

- Tính diện tích xung quanh: \(S_{xq}= p.h \), trong đó \(p\) là nửa chu vi đáy, \(d\) là trung đoạn của hình chóp đều. 

- Tính diện tích đáy theo công thức diện tích hình vuông: \(S_{hv}\) = cạnh \(\times \) cạnh.

- Tính diện tích toàn phần: \(S_{tp}= S_{xq} + S_{đ}\)

Hướng dẫn giải

Hình a:

Chu vi đáy là \(20.4 (cm)\) 

Diện tích xung quanh của hình chóp đều là:

\(S_{xq}= p.d = \dfrac{1}{2}.20.4.20 = 800(cm^2) \)

Diện tích đáy là:

\( S_{đ} = 20^2 = 400(cm^2) \)

Diện tích toàn phần của hình chóp đều là:

\( S_{tq}= S_{xq} + S_{đ} = 800 + 400 = 1200\) \((cm^2) \) 

Hình b:

Chu vi đáy là \(4.7 = 28 (cm)\) 

Diện tích xung quanh của hình chóp đều là:

\(S_{xq}= p.d = \dfrac{1}{2}.28.12 = 168 (cm^2) \)

Diện tích đáy là:

\( S_{đ} = 7^2 = 49(cm^2) \)

Diện tích toàn phần của hình chóp đều là:

\( S_{tp}= S_{xq} + S_{đ} = 168 + 49 = 217\)\(\,(cm^2) \) 

Hình c:

Do I là trung điểm của BC nên \(IC=\dfrac{BC}{2}=8cm\)

Tam giác SBC có SI là đường trung tuyến nên đồng thời là đường cao, xét tam giác SIC vuông tại I, theo định lý Pytago, ta có:

\(SI = \sqrt{SC^{2}- IC^{2}}\)\(=\sqrt{17^{2}- 8^{2}}= \sqrt{225} = 15(cm) \)

Hay trung đoạn \(d=SI=15cm\)

Chu vi đáy: \(16.4=64cm\)

Diện tích xung quanh của hình chóp đều là: 

\(S_{xq}= p.d = \dfrac{1}{2}.64.15 = 480(cm^2) \)

Diện tích đáy là:

\( S_{đ} = 16^2 = 256(cm^2) \)

Diện tích toàn phần của hình chóp đều là:

\( S_{tp}= S_{xq} + S_{đ} = 480 + 256 = 736\) \((cm^2) \)