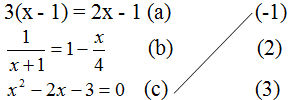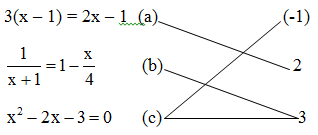Giải bài tập SGK Toán 8 Bài 1: Mở đầu về phương trình

Với mỗi phương trình sau, hãy xét xem x = -1 có là nghiệm của nó không?

a) $4x - 1 = 3x - 2$

b) $x + 1 = 2(x - 3)$

c) $2(x + 1) + 3 = 2 - x$?

Phương pháp giải

Nếu khi thay $x = -1$ vào hai vế của phương trình ta được kết quả của hai vế bằng nhau thì $x = -1$ là nghiệm của phương trình đó. 

Hướng dẫn giải

Câu a

$4x - 1 = 3x - 2$

Thay $x=-1$ vào vế trái và vế phải của phương trình ta được:

Vế trái: $4x - 1 = 4(-1) - 1 = -5$

Vế phải: $3x - 2 = 3(-1) -2 = -5$

Ta thấy kết quả vế trái bằng vế phải nên $x = -1$ là nghiệm của phương trình.

Câu b

$x + 1 = 2(x - 3);$

Thay $x=-1$ vào vế trái và vế phải của phương trình ta được:

Vế trái: $x + 1 = -1 + 1 = 0$

Vế phải: $2(x - 3) = 2(-1 - 3) = -8$

Ta thấy kết quả vế trái khác vế phải nên $x = -1$ không là nghiệm của phương trình.

Câu c

$2(x + 1) + 3 = 2 - x$

Thay $x=-1$ vào vế trái và vế phải của phương trình ta được:

Vế trái: $2(x + 1) + 3 = 2(-1 + 1) + 3 = 3$

Vế phải: $2 - x = 2 - (-1) = 3$

Ta thấy kết quả vế trái bằng vế phải nên $x = -1$ là nghiệm của phương trình.

Trong các giá trị t = -1, t = 0 và t = 1, giá trị nào là nghiệm của phương trình. $(t + 2)^2 = 3t + 4$

Phương pháp giải

Thay lần lượt các giá trị của $t$ vào hai vế của phương trình ta được kết quả hai vế bằng nhau thì giá trị đó là nghiệm của phương trình

Hướng dẫn giải

* Với $t = -1$ ta có:

$VT = {\left( {t + 2} \right)^2} = {\left( { - 1 + 2} \right)^2} =  1^2 = 1$

$VP = 3t + 4 = 3.\left( { - 1} \right) + 4 = 1$

$\Rightarrow  VT = VP$ nên $t = -1$ là nghiệm của phương trình.

* Với $t = 0$ ta có:

$VT = {\left( {t + 2} \right)^2} = {\left( {0 + 2} \right)^2} = 2^2 = 4$

$VP = 3t + 4 = 3.0 + 4 = 4$

$\Rightarrow VT = VP$ nên $t = 0$ là nghiệm của phương trình.

* Với $t = 1$ ta có:

$VT = {\left( {t + 2} \right)^2} = {\left( {1 + 2} \right)^2} =  3^2 = 9$

$VP = 3t + 4 = 3.1 + 4 = 7$

$\Rightarrow VT \ne VP$ nên $t = 1$ không là nghiệm của phương trình

Xét phương trình $x + 1 = 1 + x$. Ta thấy mọi số đều là nghiệm của nó. Người ta còn nói: Phương trình này nghiệm đúng với mọi $x$. Hãy cho biết tập nghiệm của phương trình đó.

Phương pháp giải

Áp dụng định nghĩa: 

- Nghiệm của phương trình là giá trị của ẩn $x$ thoả mãn phương trình.

- Tập nghiệm của phương trình là tập hợp tất cả các nghiệm của phương trình đó.

Hướng dẫn giải

Vì phương trình $x + 1 = 1 + x$ nghiệm đúng với mọi $x \in \mathbb R$.

Vậy tập nghiệm của phương trình trên là: $S = \mathbb R.$

Nối mỗi phương trình sau với các nghiệm của nó (theo mẫu):

Phương pháp giải

Thay các giá trị của $x=-1$, $x=2$ và $x=3$ vào từng phương trình (a), (b), (c); giá trị nào thỏa mãn phương trình thì là nghiệm của phương trình đó.

Hướng dẫn giải

 *) Xét phương trình $3(x-1)=2x-1\;\;\;\;\;(1)$

+) Thay $x=-1$ vào vế trái và vế phải của phương trình (1) ta được:

$\eqalign{ & VT = 3.\left( { - 1 - 1} \right) = 3.\left( { - 2} \right) = - 6 \cr & VP = 2.\left( { - 1} \right) - 1 = - 2 - 1 = - 3 \cr}$

$- 6 \ne  - 3 \Rightarrow VT \ne VP$

Vậy $x=-1$ không là nghiệm của phương trình (1)

+) Thay $x=2$ vào vế trái và vế phải của phương trình (1) ta được:

$\eqalign{ & VT = 3.\left( {2 - 1} \right) = 3.1 = 3 \cr & VP = 2.2 - 1 = 4 - 1 = 3 \cr}$

$3 = 3 \Rightarrow VT = VP$

Vậy $x=2$ là nghiệm của phương trình (1)

+) Thay $x=3$ vào vế trái và vế phải của phương trình (1) ta được:

$\eqalign{ & VT = 3.\left( {3 - 1} \right) = 3.2 = 6 \cr & VP = 2.3 - 1 = 6 - 1 = 5 \cr}$

$6 \ne 5 \Rightarrow VT \ne VP$

Vậy $x=3$ không là nghiệm của phương trình (1)

*) Xét phương trình $\dfrac{1}{{x + 1}} = 1 - \dfrac{x}{4}\;\;\;\;\;(2)$ 

+) Với $x=-1$ thì phương trình (2) không xác định nên $x=-1$ không là nghiệm của phương trình (2)

+) Thay $x=2$ vào vế trái và vế phải của phương trình (2) ta được:

$\eqalign{ & VT = {1 \over {2 + 1}} = {1 \over 3} \cr & VP = 1 - {2 \over 4} = 1 - {1 \over 2} = {1 \over 2} \cr}$

$\dfrac{1}{3} \ne \dfrac{1}{2} \Rightarrow VT \ne VP$

Vậy $x=2$ không là nghiệm của phương trình (2)

+) Thay $x=3$ vào vế trái và vế phải của phương trình (2) ta được:

$\eqalign{ & VT = {1 \over {3 + 1}} = {1 \over 4} \cr & VP = 1 - {3 \over 4} = {4 \over 4} - {3 \over 4} = {1 \over 4} \cr}$

$\dfrac{1}{4} = \dfrac{1}{4} \Rightarrow VT = VP$

Vậy $x=3$ là nghiệm của phương trình (2)

*) Xét phương trình ${x^2} - 2x - 3 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,(3)$

+) Thay $x=-1$ vào vế trái và vế phải của phương trình (3) ta được:

$\eqalign{ & VT = {\left( { - 1} \right)^2} - 2.\left( { - 1} \right) - 3\cr&\;\;\;\;\;\;\; = 1 + 2 - 3 = 0 \cr & VP = 0 \cr}$

$0 = 0 \Rightarrow VT = VP$

Vậy $x=-1$ là nghiệm của phương trình (3)

+) Thay $x=2$ vào vế trái và vế phải của phương trình (3) ta được:

$\eqalign{ & VT = {2^2} - 2.2 - 3 = 4 - 4 - 3 = - 3 \cr & VP = 0 \cr}$

$- 3 \ne 0 \Rightarrow VT \ne VP$

Vậy $x=2$ không là nghiệm của phương trình (3)

+) Thay $x=3$ vào vế trái và vế phải của phương trình (3) ta được:

$\eqalign{ & VT = {3^2} - 2.3 - 3 = 9 - 6 - 3 = 0 \cr & VP = 0 \cr}$

$0 = 0 \Rightarrow VT = VP$

Vậy $x=3$ là nghiệm của phương trình (3)

Hai phương trình $x = 0$ và $x(x - 1) = 0$ có tương đương không? Vì sao?

Phương pháp giải

Áp dụng định nghĩa: Hai phương trình tương đương nếu chúng có cùng một tập nghiệm.

Bước 1: Ta tìm tập nghiệm của hai phương trình $x = 0$ và $x(x - 1) = 0$ 

Giả sử phương trình $x = 0$ có tập nghiệm là $S_1$; phương trình $x(x - 1) = 0$ có tập nghiệm $S_2$

Bước 2: So sánh $S_1$ và $S_2$

Bước 3: Kết luận

- Nếu $S_1=S_2$ thì hai phương trình tương đương.

- Nếu $S_1\ne S_2$ thì hai phương trình không tương đương.

Hướng dẫn giải

Phương trình $x = 0$ có tập nghiệm ${S_1} = {\rm{\{ }}0\}$.

Xét phương trình $x(x - 1) = 0$.

Ta có một tích bằng $0$ khi một trong hai thừa số bằng $0$ tức là:

$x(x - 1) = 0$ khi $x = 0$ hoặc $x = 1$.

Vậy phương trình $x(x - 1) = 0$ có tập nghiệm ${S_2} = {\rm{\{ }}0;1\}$

Vì ${S_1} \ne {S_2}$ nên hai phương trình không tương đương.