Giải bài tập SGK Toán 8 Bài 2: Hình hộp chữ nhật (tiếp theo)

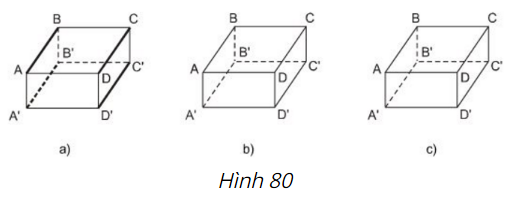
Người ta tô đậm những cạnh song song và bằng nhau của một hình hộp chữ nhật như ở hình 80a. Hãy thực hiện điều đó với hình 80b và 80c.

Phương pháp giải

Hai đường thẳng \(a\) và \(b\) gọi là song song với nhau nếu chúng nằm trong cùng một mặt phẳng và không có điểm chung.

Hướng dẫn giải

Các cạnh song song và bằng nhau của một hình hộp chữ nhật trên hình 80b, 80c là:

+ BC = B'C' = AD = A'D'

+ AA’ = BB’ = CC’ = DD’

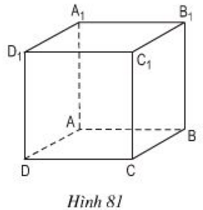
\(ABCD.A{_1}{B_1}{C_1}{D_1}\)  là một hình lập phương (h.81). Quan sát hình và cho biết :

a) Những cạnh nào song song với cạnh \(C_1C\)?

b) Những cạnh nào song song với cạnh  \(A_1D_1\)? 

Phương pháp giải

Hai đường thẳng \(a\) và \(b\) gọi là song song với nhau nếu chúng nằm trong cùng một mặt phẳng và không có điểm chung.

Hướng dẫn giải

Những cạnh song song với cạnh \(CC_1\) là : \(A{A_1};{\rm{ }}B{B_1};{\rm{ }}D{D_1}\)

Những cạnh song song với cạnh \({A_1}{D_1}\) là \({B_1}{C_1};{\rm{ }}BC;{\rm{ }}AD.\)

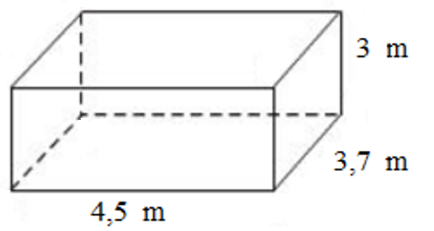
Một căn phòng dài \(4,5m\), rộng \(3,7m\) và cao \(3,0m\). Người ta muốn quét vôi trần nhà và bốn bức tường. Biết rằng tổng diện tích các cửa là \(5,8{m^2}\). Hãy tính diện tích cần quét vôi.

Phương pháp giải

Diện tích cần quét vôi = diện tích bốn bức tường + diện tích trần - diện tích cửa.

Hay: Diện tích cần quét vôi = diện tích xung quanh + diện tích trần - diện tích cửa.

Tính diện tích xung quanh theo công thức \( S_{xq}=(a+b)\times 2 \times c \), với \(a\) là chiều dài, \(b\) là chiều rộng, \(c\) là chiều cao.

Hướng dẫn giải

Ta có: Diện tích cần quét vôi bằng diện tích bốn bức tường + diện tích trần - diện tích cửa. 

Mà diện tích 4 bức tường chính là diện tích xung quanh của hình hộp (hay căn phòng)

Nên diện tích cần quét vôi = diện tích xung quanh + diện tích trần - diện tích cửa. 

Diện tích trần nhà là:

\( 4,5 \times  3,7 = 16,65 (m^2)\)

Diện tích xung quanh căn phòng là:

\(2.(4,5 + 3,7). 3= 49,2(m^2) \)

Diện tích cần quét vôi là:

\(16,65 + 49,2 - 5,8 = 60,05 (m^2) \)

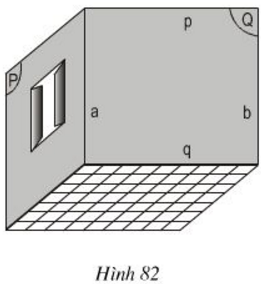
Hình 82 vẽ một phòng ở. Quan sát hình và giải thích vì sao:

a) Đường thẳng \(b\) song song với mp \((P)\)?

b) Đường thẳng \(p \) song song với sàn nhà?

Phương pháp giải

Dựa vào lý thuyết về đường thẳng song song với mặt phẳng.

Khi đường thẳng \(d\) không nằm trong mặt phẳng \((ABCD)\) mà \(d\) song song với đường thẳng của mặt phẳng này thì ta nói đường thẳng \(d\) song song với mặt phẳng \((ABCD)\).

Hướng dẫn giải

a) Ta có  \( a\subset mp(P);\; a\, //\, b \) .

 Mặt khác \(b\) không thuộc mp\((P) \)

 Do đó, \( b //mp (P) \) .

(trong đó mp là mặt phẳng) 

b) Ta có \(p \)  không thuộc sàn nhà và đường thẳng \(p\) song song với đường thẳng \( q\)  trong sàn nhà nên \(p\) song song với sàn nhà.

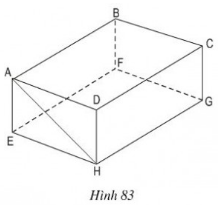
Hình hộp chữ nhật \(ABCD.EFGH\) (h83) có cạnh \(AB\) song song với mặt phẳng \((EFGH)\).

a) Hãy kể tên các cạnh khác song song với mặt phẳng \((EFGH)\)

b) Cạnh \(CD\) song song với những mặt phẳng nào?

c) Đường thẳng \(AH\) không song song với mặt phẳng \((EFGH)\), hãy chỉ ra mặt phẳng song song với đường thẳng đó.

Phương pháp giải

Áp dụng các định nghĩa:

- Hình hộp chữ nhật:

+ Hình hộp chữ nhật là hình không gian có 6 mặt đều là những hình chữ nhật

+ Hai mặt đối diện nhau được xem là hai mặt đáy của  hình hộp chữ nhật, các mặt còn lại gọi là mặt bên

- Khi đường thẳng \(d\) không nằm trong mặt phẳng \((ABCD)\) mà \(d\) song song với đường thẳng của mặt phẳng này thì ta nói đường thẳng \(d\) song song với mặt phẳng \((ABCD)\).

Hướng dẫn giải

a) \(BC // FG\)  nên suy ra \( BC //mp (EFGH)\)

\(CD // HG\)  nên suy ra \(CD //mp (EFGH)\) 

\(AD  // EH\) nên suy ra \(AD  //mp (EFGH)\).  

Vậy ngoài \(AB\), các cạnh song song với mặt phẳng \((EFGH)\) là \(BC; CD; AD\).

b) \(CD // AB\) nên suy ra \( CD //mp (ABFE)\) và \(CD //mp (EFGH)\) (theo ý a)

Vậy cạnh \(CD\) song song với hai mặt phẳng \((ABFE)\) và \((EFGH)\).

c) Vì \(AB // HG, AB = HG\) nên suy ra \(ABGH\) là hình bình hành.

Do đó ta có \(AH // BG\) (tính chất hình bình hành).

Từ đó suy ra mặt phẳng song song với đường thẳng \(AH\) là mặt phẳng \((BCGF)\).