Giải bài tập SGK Toán 8 Bài 6: Thể tích của hình lăng trụ đứng

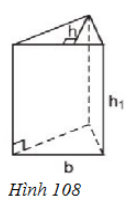
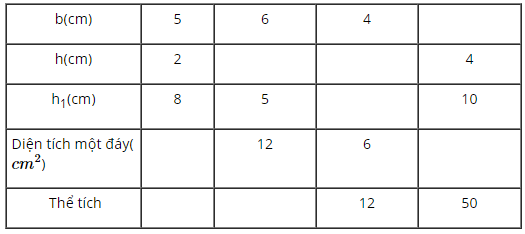
Quan sát hình 108 rồi điền số thích hợp vào các ô trống ở bảng sau:

Phương pháp giải

Áp dụng các công thức:

Thế tích: $V= S.h_1$, trong đó $S$ là diện tích đáy, $h_1$ là chiều cao hình lăng trụ

Diện tích đáy : $S = \dfrac{1}{2}b.h$ với $h$ là chiều cao ứng với cạnh đáy $b.$

Hướng dẫn giải

Ta có: Diện tích đáy: $S = \dfrac{1}{2}b.h$.

Thể tích  $V= S.h_1$ 

Ở cột 2: $S = \dfrac{1}{2} b.h = \dfrac{1}{2}. 5.2 = 5$ 

$V= S.h_1 = 5. 8 = 40$

Ở cột 3: $S = \dfrac{1}{2}. b.h$$\, \Rightarrow h =\dfrac{2.S}{b} =\dfrac{2.12}{6}=  4$

$V= S.h_1 = 12. 5 = 60$

Ở cột 4: $h = \dfrac{2.S}{b} = \dfrac{2.6}{4}=  3$

$V = S.h_1 \Rightarrow h_1 =\dfrac{V}{S} =\dfrac{12}{6}=  2$

Ở cột 5: $V = S.h_1 \Rightarrow  S=\dfrac{V}{h_1} =\dfrac{50}{10}= 5$

 $S =\dfrac{1}{2} b.h \Rightarrow b = \dfrac{2.S}{h} = \dfrac{2.5}{4} = 2,5$

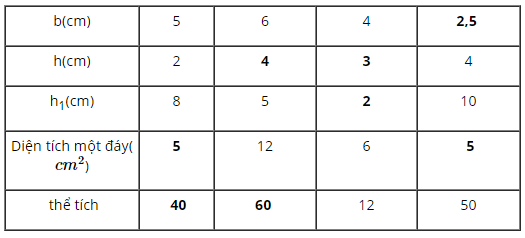
Vậy có kết quả sau khi điền vào bảng sau là:

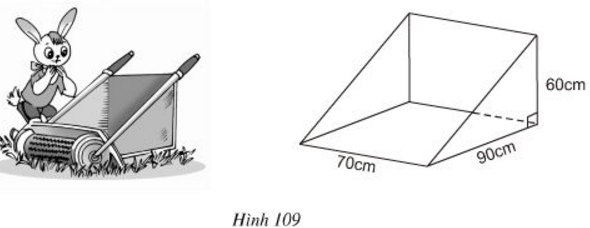
Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác (h.109). Hãy tính dung tích của thùng.

Phương pháp giải

Áp dụng công thức:

Thể tích: $V= S.h$, trong đó $S$ là diện tích đáy, $h$ là chiều cao.

Đáy là tam giác vuông nên diện tích đáy :  $S = \dfrac{1}{2}a.b$, trong đó $a,\; b$ là độ dài hai cạnh góc vuông.

Hướng dẫn giải

Lăng trụ đứng tam giác có đáy là tam giác vuông nên diện tích đáy là :

$S = \dfrac{1}{2}. 60.90 = 2700 (cm^2)$ 

Thể tích lăng trụ là:

$V = S. h = 2700.70 = 189000 (cm^3)$ 

Vậy dung tích của thùng là $189000 (cm^3)$.

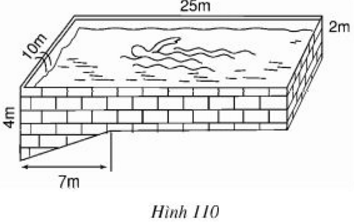
Các kích thước của một bể bới được cho trên hình 110 (mặt nước có dạng hình chữ nhật). Hãy tính xem bể chứa được bao nhiêu mét khối nước khi nó đầy ắp nước?

Phương pháp giải

- Bể bơi được chia thành hai phần: phần hình hộp chữ nhật với các kích thước là $10m, \;25m,\; 2m$ và phần hình lăng trụ đứng với đáy là tam giác vuông có hai cạnh góc vuông là $2m,\; 7m$ và chiều cao $10m$.

- Tính thể tích hình hộp chữ nhật: $V= a.b.c$, trong đó $a,\; b,\; c$ là các kích thước của hình hộp chữ nhật.

- Thể tích lăng trụ: $V = S. h$, trong đó $S$ là diện tích đáy, $h$ là chiều cao.

Hướng dẫn giải

Bể bơi được chia thành hai phần: phần hình hộp chữ nhật với các kích thước là $10m, \;25m,\; 2m$ và phần hình lăng trụ đứng với đáy là tam giác vuông có hai cạnh góc vuông là $2m,\; 7m$ và chiều cao $10m$.

Thể tích hình hộp chữ nhật là:

$V =  10.25.2 = 500 (m^3)$

Thể tích lăng trụ đứng tam giác là:

$V = S.h = \dfrac{1}{2}. 2.7.10 = 70$ $(m^3)$

Vậy bể bơi có thể chứa số mét khối nước khi đầy ắp nước là:

$500 +70 = 570(m^3)$

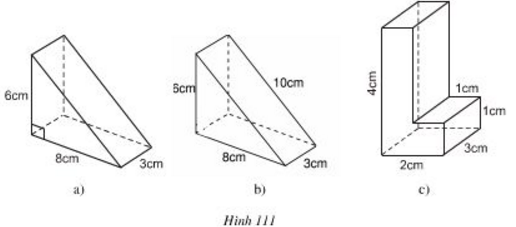
Các hình a, b, c (h.111) gồm một hoặc nhiều lăng trụ đứng. Hãy tính thể tích và diện tích toàn phần của chúng theo các kích thước đã cho trên hình.

Phương pháp giải

Áp dụng các công thức: 

- Diện tích xung quanh: $S_{xq} =2p.h$, trong đó $p$ là nửa chu vi đáy, $h$ là chiều cao.

- Diện tích toàn phần = diện tích xung quanh + diện tích hai đáy.

Hướng dẫn giải

Hình a

Là lăng trụ đứng có chiều cao là $3cm$ và đáy là tam giác vuông có hai cạnh góc vuông là $6cm,\; 8cm$. 

Suy ra cạnh huyền là $\sqrt{6^{2}+8^{2}} = \sqrt{36+64} = \sqrt{100} = 10$ $(cm)$.

Diện tích đáy là :  $S = \dfrac{1}{2}6 . 8 = 24(cm^2)$

Thể tích lăng trụ là: $V = S.h = 24.3 = 72(cm^3)$

Diện tích xung quanh lăng trụ là:

$S_{xq} =2p.h = (6+8+10).3 = 24.3$$=72$ $(cm^2)$

Diện tích toàn phần lăng trụ là:

$S_{tp} =S_{xq}+2. S_{đ} = 72 +2.24 =120$ $(cm^2)$

Hình b

Là lăng trụ đứng tam giác có ba kích thước là $6cm,\, 8cm, \,10cm$; chiều cao lăng trụ là $3cm$.

Vì $6^2 + 8^2 = 36 + 64 = 100 = 10^2$ nên đáy lăng trụ là tam giác vuông có hai cạnh góc vuông là $6cm,\, 8cm$. Do đó, bài toán này quay về bài toán ở hình a, ta thu được kết quả:

$V= 72cm^3; \quad S_{xq} = 72 cm^2;$$\quad S_{tp} =120(cm^2)$.

Hình c

Là hình gồm hai lăng trụ đứng: Hình lăng trụ một là hình hộp chữ nhật có các kích thước $4cm, \; 1cm,\; 3cm$ ; hình lăng trụ hai là hình hộp chữ nhật có các kích thước $1cm,\;1cm, \; 3cm$.

Thể tích lăng trụ một là: $V_1 = 4.1.3 =12 (cm^3)$

Thể tích lăng trụ hai là: $V_2 = 1.1.3 =3 (cm^3)$

Thể tích lăng trụ đã cho là

$V = V_1+ V_2 = 12 +3 =15 (cm^3)$

Diện tích xung quanh của lăng trụ một là:

$S_{xq1} = 2.(3+1).4 =32 (cm^2)$

Diện tích một đáy của lăng trụ một là:

$S_{đ1} = 3.1 =3 (cm^2)$

Diện tích toàn phần của lăng trụ một là:

$S_{tp1} =S_{xq1} +2. S_{đ1} = 32 +2.3 =38$ $(cm^2)$

Diện tích xung quanh của lăng trụ hai là:

$S_{xq2} = 2.(1+3).1 =8 (cm^2)$

Diện tích một đáy của lăng trụ hai là:

$S_{đ2} = 3.1 =3 (cm^2)$

Diện tích toàn phần của lăng trụ hai là:

$S_{tp2} =S_{xq2} +2. S_{đ2} = 8 +2.3=14$ $(cm^2)$

Diện tích toàn phần của lăng trụ đã cho bằng tổng diện tích toàn phần của lặng trụ 1 và 2 trừ đi 2 phần diện tích chung là hình chữ nhật với các kích thước $1cm,\; 3cm$. Do đó:

$S_{tp} =S_{tp1} +S_{tp2} - 2. S_{hcn}$ 

$=38 + 14 - 2.3.1 =46 (cm^2)$