Giải bài tập SGK Toán 8 Bài 7: Hình bình hành

Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?

Phương pháp giải

Áp dụng dấu hiệu nhận biết hình bình hành

• Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
• Tứ giác có các cạnh đối bằng nhau là hình bình hành.

Hướng dẫn giải

Cả ba tứ giác đều là hình bình hành.

- Tứ giác $ABCD$ là hình bình hành vì có

$AB // CD$ và $AB = CD =3$ (dấu hiệu nhận biết hình bình hành)

- Tứ giác $EFGH$ là hình bình hành vì có

$EH // FG$ và $EH = FH = 3$  (dấu hiệu nhận biết hình bình hành)

- Tứ giác $MNPQ$

$MN$ và $PQ$ là cạnh huyền của tam giác vuông có hai cạnh góc vuông là $1$ và $5$.

Áp dụng định lí Py-ta-go ta có: $MN = PQ = \sqrt {{5^2} + {1^2}}  = \sqrt {26}$

$MQ$ và $NP$ là cạnh huyền của tam giác vuông có hai cạnh góc vuông là $1$ và $3$

Áp dụng định lí Py-ta-go ta có: $MQ = NP = \sqrt {{3^2} + {1^2}}  = \sqrt {10}$

Do đó $MNPQ$ là hình bình hành vì có $MN = PQ$ và $MQ = NP$ ( dấu hiệu nhận biết hình bình hành).

Cho hình bình hành $ABCD$. Gọi  $E$ là trung điểm của $AD$, $F$ là trung điểm của $BC$. Chứng minh rằng $BE = DF$

Phương pháp giải

Áp dụng

• Hình bình hành có các cặp cạnh đối song song và bằng nhau.
• Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Hướng dẫn giải

$ABCD$ hình bình hành nên  $DE // BF$ và $AD=BC$

$E$ là trung điểm của $AD$ (giả thiết) nên $DE = \dfrac{1}{2}AD$ (tính chất trung điểm)

$F$ là trung điểm của $BC$ (giả thiết) nên $BF= \dfrac{1}{2}BC$ (tính chất trung điểm)

Mà $AD=BC$ (chứng minh trên) nên $DE=BF$

Tứ giác $BEDF$ có $DE//BF$ và $DE=BF$ (chứng minh trên)

$\Rightarrow$ Tứ giác $BEDF$ là hình bình hành (theo dấu hiệu nhận biết hình bình hành)

Vậy theo tính chất hình bình hành ta được $BE = DF$ (đpcm)

Cho hình bình hành $ABCD$ ($AB > BC$). Tia phân giác của góc $D$ cắt $AB$ ở $E$, tia phân giác của góc $B$ cắt $CD$ ở $F$

a) Chứng minh rằng $DE // BF$

b) Tứ giác $DEBF$ là hình gì? Vì sao?

Phương pháp giải

Áp dụng

• Hình bình hành có các góc đối bằng nhau. 
• Dấu hiệu nhận biết hình bình hành: Tứ giác có các cạnh đối song song là hình bình hành.

Hướng dẫn giải

Câu a

 Vì $ABCD$ là hình bình hành (giả thiết)

$\Rightarrow \widehat {ABC} = \widehat {ADC}$ (tính chất hình bình hành) (1)

Vì $BF$ là tia phân giác $\widehat {ABC}$ (giả thiết)

$\Rightarrow$$\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}$ (tính chất tia phân giác) (2)

Vì $DE$ là tia phân giác $\widehat {ADC}$ (giả thiết)

$\Rightarrow$ $\widehat {{D_1}} = \widehat {{D_2}} = \dfrac{{\widehat {ADC}}}{2}$ (tính chất tia phân giác) (3)

Từ (1), (2), (3) $\Rightarrow \widehat {{D_2}} = \widehat {{B_1}}$  (4)

Có $AB//DC$ (vì $ABCD$ là hình bình hành)

Suy ra: $\widehat {{B_1}} = \widehat {{F_1}}$ (so le trong)   (5)

Từ (4) và (5) suy ra $\widehat {{F_1}} = \widehat {{D_2}}$ mà hai góc này ở vị trí đồng vị nên $DE//BF$ (dấu hiệu nhận biết hai đường thẳng song song)

Câu b

$ABCD$ là hình bình hành (giả thiết)

$\Rightarrow$$AB // CD$ (tính chất hình bình hành) hay $BE // DF$

Xét tứ giác $DEBF$ có $BE // DF$ (chứng minh trên) và $DE//BF$ (theo câu a)

Suy ra tứ giác $DEBF$ là hình bình hành (dấu hiệu nhận biết hình bình hành)

Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Phương pháp giải

Áp dụng dấu hiệu nhận biết hình bình hành.

Hướng dẫn giải

Câu a: Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bàng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

Câu b: Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

Câu c: Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành

Câu d: Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành

Cho hình 72, trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng

Phương pháp giải

Áp dụng: Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.

Hướng dẫn giải

Câu a

Xét hai tam giác vuông $AHD$ và $CKB$ có

$AD = CB$ (vì $ABCD$ là hình bình hành)

$\widehat {ADH} = \widehat {CBK}$ (hai góc ở vị trí so le trong, $AD//BC$)

$\Rightarrow$ $∆AHD =  ∆CKB$ (cạnh huyền- góc nhọn)

$\Rightarrow$ $AH = CK$ ($2$ cạnh tương ứng)

Ta có

$\left\{ \begin{array}{l} AH \bot B{\rm{D}}\\ CK \bot B{\rm{D}} \end{array} \right.\left( \text{giả thiết} \right) \Rightarrow AH//CK$

Xét tứ giác $AHCK$ có

$\left\{ \begin{array}{l} AH//CK\\ AH = CK \end{array} \right.\left( \text{chứng minh trên} \right)$

$\Rightarrow$ tứ giác $AHCK$ là hình bình hành (dấu hiệu nhận biết hình bình hành).

Câu b

Xét hình bình hành $AHCK$ có $O$ là trung điểm của $HK$ (giả thiết)

$\Rightarrow$ $O$ là giao điểm của hai đường chéo $AC$ và $HK$ của hình bình hành (tính chất hình bình hành)

Hay $A,O,C$ thẳng hàng.

Tứ giác $ABCD$ có $E, F, G, H$ theo thứ tự là trung  điểm của các cạnh $AB, BC, CD, DA.$ Tứ giác $EFGH$ là hình gì? Vì sao?

Phương pháp giải

Áp dụng

• Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
• Dấu hiệu nhận biết hình bình hành: Tứ giác cặp cạnh đối song song và bằng nhau là hình bình hành.

Hướng dẫn giải

Xét $\Delta ABC$ có $EA=EB$ và $FB=FC$ nên $EF$ là đường trung bình của  $\Delta ABC$ suy ra $EF // AC$ và $EF = \dfrac{{AC}}{2}$       (1)

Xét $\Delta ADC$ có $HA=HD$ và $GD=GC$ nên $HG$ là đường trung bình của $\Delta ADC$ suy ra $HG // AC$ và $HG = \dfrac{{AC}}{2}$         (2)

Từ (1) và (2) suy ra $EF//HG$ và $EF = HG$

Tứ giác $EFGH$ có $EF//HG$ và $EF = HG$ nên là hình bình hành (dấu hiệu nhận biết hình bình hành).

Vậy tứ giác $EFGH$ là hình bình hành

Cho hình bình hành $ABCD.$ Gọi $I, K$ theo thứ tự là trung điểm của $CD, AB.$ Đường chéo $BD$ cắt $AI, CK$ theo thứ tự ở $M$ và $N.$ Chứng minh rằng:

a) $AI // CK$

b) $DM = MN = NB$

Phương pháp giải

Áp dụng

• Hình bình hành có các cặp cạnh đối song song và bằng nhau.
• Dấu hiệu nhận biết hình bình hành: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
• Định lí: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba

Hướng dẫn giải

Câu a

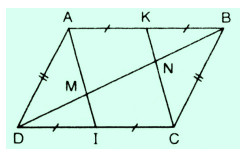
 Vì $ABCD$ là hình bình hành (giả thiết) 

$\Rightarrow \left\{ \begin{array}{l} AB = C{\rm{D}}\\ AB//C{\rm{D}} \end{array} \right.$ (tính chất hình bình hành)

Mà $I, K$ theo thứ tự là trung điểm của $CD, AB$ (giả thiết)

$\Rightarrow \left\{ \begin{array}{l} AK =KB= \dfrac{{AB}}{2}\\ IC =ID= \dfrac{{DC}}{2} \end{array} \right.$ (tính chất trung điểm)

Mà $AB=CD$ (chứng minh trên) nên $\dfrac{AB}2=\dfrac{CD}2$

$\Rightarrow AK = IC$

Lại có: $AB//DC\left( \text{chứng minh trên} \right)$ $\Rightarrow AK//IC$ 

Tứ giác $AICK$ có:

$\left\{ \begin{array}{l} AK//IC\\ AK = IC \end{array} \right.\left( \text{chứng minh trên} \right)$

$\Rightarrow$ Tứ giác $AICK$ là hình bình hành (dấu hiệu nhận biết hình bình hành)

$\Rightarrow AI // CK$ (tính chất hình bình hành)

Câu b

 $∆DCN$ có $DI = IC$ (chứng minh trên), $IM // CN$ (vì $AI // KC$)

$\Rightarrow  DM = MN$ (1) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)

 Xét $∆ABM$ có $AK = KB$ (chứng minh trên) và $KN // AM$ ( vì $AI // CK$)

$\Rightarrow  MN = NB$ (2) (Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba)

Từ (1) và (2) $\Rightarrow DM = MN = NB$