Giải bài tập SGK Toán 8 Bài 8: Đối xứng tâm

Vẽ điểm \(A'\) đối xứng với \(A\) qua \(B\), vẽ điểm \(C'\) đối xứng với \(C\) qua \(B\) (h.\(81\))

Phương pháp giải

Áp dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.

Hướng dẫn giải

 Cách vẽ

Vẽ đoạn thẳng \(AB\) rồi kéo dài về phía \(B,\) chọn điểm \(A'\) sao cho \(B\) là trung điểm của \(AA'.\) Ta được điểm \(A'\) đối xứng với \(A\) qua \(B.\)

Vẽ đoạn thẳng \(CB\) rồi kéo dài về phía \(B.\) Chọn điểm \(C'\), sao cho \(B\) là trung điểm của \(CC'\). Ta được điểm \(C'\) đối xứng với \(C\) qua \(B.\) 

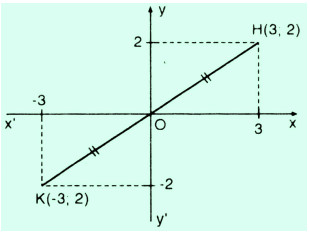
Trong mặt phẳng tọa độ, cho điểm \(H\) có tọa độ \((3; 2)\). Hãy vẽ điểm \(K\) đối xứng với \(H\) qua gốc tọa độ và tìm tọa độ \(K\)

Phương pháp giải

Định nghĩa: Hai điểm \(A\) và \(A'\) gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của \(AA'.\)

Hướng dẫn giải

Trên mặt phẳng tọa độ \(xOy\), xác định điểm \(H\) có tọa độ \((3 ; 2)\). Như vậy ta đã có hai điểm \(O\) và \(H\). Để vẽ điểm \(K\) đối xứng với điểm \(H\) qua gốc tọa độ \(O\), ta nối đoạn thẳng \(OH\) sau đó lấy điểm \(K\) sao cho \(O\) là trung điểm của đoạn \(KH\)

Qua \(K\) ta dựng các đường thẳng song song với trục \(Ox\) và trục \(Oy\) ta tìm được tọa độ của điểm \(K\)

Khi đó điểm \(K\) có tọa độ \((-3 ; -2)\)

Cho hình bình hành \(ABCD\). Gọi \(E\) là điểm đối xứng với \(D\) qua điểm \(A\), gọi \(F\) là điểm đối xứng với \(D\) qua điểm \(C\). Chứng minh rằng điểm \(E\) đối xứng với điểm \(F\) qua điểm \(B\)

Phương pháp giải

Áp dụng

• Hình bình hành có các cặp cạnh đối song song và bằng nhau.
• Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.
• Tiên đề ơclit: Qua một điểm ở ngoài đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

Hướng dẫn giải

Vì \(ABCD \) là hình bình hành (giả thiết)

\( \Rightarrow A{\rm{D}}//BC, A{\rm{B}}//DC,\)\( A{\rm{D}}=BC, A{\rm{B}}=DC \) (tính chất hình bình hành)

Mà \(E \in A{\rm{D}}\) (giả thiết) \( \Rightarrow AE//BC\)

Vì \(E\) là điểm đối xứng với \(D\) qua điểm \(A\) (giả thiết)

\( \Rightarrow AE = A{\rm{D}}\) (tính chất hai điểm đối xứng qua 1 điểm)

\( \Rightarrow \) \(AE = BC\) (cùng bằng \(AD\))

Kết hợp với \(AE//BC\) (chứng minh trên) 

\( \Rightarrow \) Tứ giác \(ACBE\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(BE // AC, BE = AC\)       (1) (tính chất hình bình hành)

Ta có: \(AB//DC\) (chứng minh trên) \(\Rightarrow AB//CF\) 

Vì \(F\) là điểm đối xứng với \(D\) qua điểm \(C\) (giả thiết)

\( \Rightarrow CD = CF\) (tính chất hai điểm đối xứng qua 1 điểm)

\( \Rightarrow AB = CF\) (cùng bằng \(DC\))

Kết hợp với \(AB//CF\) (chứng minh trên)

\( \Rightarrow \) Tứ giác \(ACFB\) là hình bình hành (dấu hiệu nhận biết hình bình hành).

\( \Rightarrow \) \(BF // AC, BF = AC\)       (2) (tính chất hình bình hành)

Từ (1) và (2) suy ra \(BE\) và \(BF\) cùng song song với \(AC\) và cùng đi qua điểm \(B\) nên theo tiên đề Ơclit \(BE\) trùng \(BF\) hay \(B, E, F\) thẳng hàng.

Lại có: \(BE\) = \(BF\) (cùng bằng \(AC\)) do đó \(B\) là trung điểm của \(EF\)

Vậy \(E\) đối xứng với \(F\) qua \(B\)

Cho hình 82, trong đó MD // AB và ME // AC. Chứng minh rằng điểm A đối xứng với  điểm M qua I. 

Phương pháp giải

Áp dụng

• Dấu hiệu nhận biết hình bình hành: Tứ giác có các cạnh đối song song.
• Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường.
• Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.

Hướng dẫn giải

Ta có \(MD // AE\) (vì \(MD // AB\)) (giả thiết).

\(ME // AD\) (vì \(ME // AC\)) (giả thiết).

\( \Rightarrow \) \(AEMD\) là hình bình hành (dấu hiệu nhận biết hình bình hành)

Lại có, \(I\) là trung điểm của \(DE\) (giả thiết) mà \(DE\) và \(AM\) là hai đường chéo của hình bình hành \(AEMD\) nên \(I\) cũng là trung điểm của \(AM\) (theo tính chất hình bình hành).

Do đó \(A\) đối xứng với \(M\) qua \(I\) (theo định nghĩa hai điểm đối xứng qua \(1 \) điểm).

Cho góc vuông \(xOy\), điểm \(A\) nằm trong góc đó. Gọi \(B\) là điểm đối xứng với \(A\) qua \(Ox\), gọi \(C\) là điểm đối xứng với \(A\) qua \(Oy\). Chứng minh rằng điểm \(B\) đối xứng với điểm \(C\) qua \(O\)

Phương pháp giải

Hai điểm \(A\) và \(A'\) gọi là đối xứng nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của \(AA'\)

Hướng dẫn giải

\(A\) đối xứng với \(B\) qua \(Ox\) (giả thiết) nên \(Ox\) là đường trung trực của \(AB\) 

\( \Rightarrow \)  \(OA = OB\)  (tính chất đường trung trực của đoạn thẳng)    (1)

\(\Rightarrow \Delta AOB\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)

Do đó \(Ox\) vừa là đường trung trực đồng thời là phân giác của \( \Delta AOB\)

\( \Rightarrow \) \(\widehat O_1=\widehat O_2\)   (3)

\(A\) đối xứng với \(C\) qua \(Oy\) (giả thiết) nên \(Oy\) là đường trung trực của \(AC\)

\( \Rightarrow \) \(OA = OC\)   (tính chất đường trung trực của đoạn thẳng)     (2)

\(\Rightarrow \Delta AOC\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)

Do đó \(Oy\) vừa là đường trung trực đồng thời là phân giác của \( \Delta AOC\)

\( \Rightarrow \) \(\widehat O_3=\widehat O_4\)    (4) 

Từ (3) và (4) \( \Rightarrow \) \(\widehat O_1+\widehat O_2+\widehat O_3+\widehat O_4\)\(=2\widehat O_2+2\widehat O_3=2(\widehat O_2+\widehat O_3)\)\(=2\widehat {xOy}=2.90^0=180^0\) 

Do đó \(B, O, C\) thẳng hàng   (**)

Từ (1) và (2) \( \Rightarrow \) \(OB = OC\) (*)

Từ (*) và (**) \( \Rightarrow \) \(B\) đối xứng với \(C\) qua \(O\).

Cho hình bình hành \(ABCD\), \(O\) là giao điểm của hai đường chéo. Một đường thẳng đi qua \(O\) cắt các cạnh \(AB\) và \(CD\) theo thứ tự ở \(M\) và \(N\). Chứng minh rằng điểm \(M\) đối xứng với điểm \(N\) qua \(O\)

Phương pháp giải

Áp dụng

• Hình bình hành có các cạnh đối song song.
• Hai điểm gọi là đối xứng với nhau qua điểm \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó.

Hướng dẫn giải

Vì \( ABCD\) là hình bình hành có O là giao điểm hai đường chéo (giả thiết).

\( \Rightarrow AB//DC\) và \(BO=DO\) (tính chất hình bình hành) 

\( \Rightarrow\) \(\widehat{B_{1}} = \widehat{D_{1}}\) (so le trong)

Xét \(\Delta BOM\) và \(\Delta DON\) có:

 \(\widehat{B_{1}} = \widehat{D_{1}}\) (chứng minh trên)

 \(BO = DO\) (chứng minh trên)

 \(\widehat{O_{1}} = \widehat{O_{2}}\) (đối đỉnh) 

\( \Rightarrow\) \( ∆BOM = ∆DON (g.c.g)\)

\( \Rightarrow\) \(OM = ON\) (hai cạnh tương ứng).

\( \Rightarrow\) \(O\) là trung điểm của \(MN\) (dấu hiệu nhận biết trung điểm)

\( \Rightarrow\) \(M \) đối xứng với \(N\) qua \(O\).

Trong các hình vẽ sau, hình nào có tâm đối xứng?

a) Đoạn thẳng \(AB\) (h.\(83a\))

b) Tam giác đều \(ABC\) (h.\(83b\))

c) Biển cấm đi ngược chiều (h.\(83c\))

d) Biển chỉ hướng đi vòng tránh chướng ngại vật (h.\(83d\))

Phương pháp giải

Áp dụng định nghĩa: Hình có tâm đối xứng

Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\)

Hướng dẫn giải

Hình \(83a\) có tâm đối xứng là trung điểm của đoạn thẳng \(AB\).

Hình \(83b\) không có tâm đối xứng. 

Giải thích: Nếu gọi \(O\) là giao điểm của \(3\) đường trung trực trong \(ΔABC\) (là tam giác đều) thì điểm đối xứng của \(3\) điểm \(A, B, C\) qua \(O\) không thuộc \(ΔABC\) \(\Rightarrow \) Hình này không có tâm đối xứng.

Hình \(83c\) có tâm đối xứng là tâm của đường tròn.

Hình \(83d\) không có tâm đối xứng.

Giải thích: Nếu gọi \(O\) là tâm đường tròn. Thì có vô số điểm thuộc hình dấu "\( \Rightarrow \)" sẽ không có điểm đối xứng thuộc hình dấu "\( \Rightarrow \)" nên hình này cũng không có tâm đối xứng.

Các câu sau đúng hay sai ?

a) Tâm đối xứng của một đường thẳng là điểm bất kì của đường thẳng đó.

b) Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.

c) Hai tam giác đối xứng với nhau qua một điểm thì có chu vi bằng nhau.

Phương pháp giải

Áp dụng định nghĩa: Hình có tâm đối xứng

Điểm \(O\) gọi là tâm đối xứng qua hình \(H\) nếu điểm đối xứng với mỗi điểm thuộc hình \(H\) qua điểm \(O\) cũng thuộc hình \(H.\)

Hướng dẫn giải

Câu a: Đúng, vì nếu lấy một điểm \(O\) bất kì trên đường thẳng thì nó chia đường thẳng đó thành hai tia và với bất kì một điểm \(M\), trên tia này cũng luôn có một điểm \(M'\) đối xứng với nó qua \(O\) trên tia kia.

Câu b: Sai, vì nếu lấy điểm đối xứng của 1 đỉnh bất kì của tam giác qua trọng tâm thì điểm đối xứng này không thuộc tam giác. 

Giả sử tam giác \(ABC\) có trọng tâm \(G.\) 

Khi đó điểm \(A’\) đối xứng với \(A\) qua \(G\) không thuộc tam giác.

Câu c: Đúng, vì hai tam giác đối xứng với nhau qua một điểm thì chúng bằng nhau và hai tam giác bằng nhau có chu vi bằng nhau.