Giải bài tập SGK Toán 8 Bài 6: Diện tích đa giác
Nội dung hướng dẫn Giải bài tập SGK Hình học 8 Bài 6 dưới đây sẽ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức về Diện tích đa giác. Mời các em cùng theo dõi.
Mục lục nội dung

1. Giải bài 37 trang 130 SGK Toán 8 tập 1
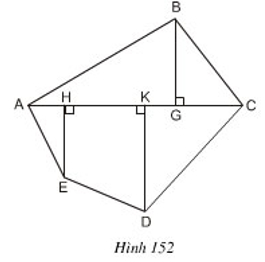
Thực hiện các phép đo cần thiết (chính xác đến từng mm) để tính diện tích hình \(ABCDE\) (h.\(152\)).
Phương pháp giải
Ta chia đa giác đó thành tam giác \(ABC\), hai tam giác vuông \(AHE, DKC\) và hình thang vuông \(HKDE.\) Sau đó, áp dụng công thức tính diện tích tam giác, hình thang.
Hướng dẫn giải
Đa giác \(ABCDE\) được chia thành tam giác \(ABC\), hai tam giác vuông \(AHE, DKC\) và hình thang vuông \(HKDE.\)
Thực hiện phép đo chính xác đến mm ta được:
\(BG= 19mm, AC = 48mm, \)\(AH = 8mm, HK = 18mm\)
\(KC = 22mm, EH = 16mm, \)\(KD = 23mm\)
\({S_{ABC}}= \dfrac{1}{2}.BG. AC = \dfrac{1}{2}. 19.48 = 456\) \((m{m^2})\)
\({S_{AHE}}=\dfrac{1}{2} AH. HE = \dfrac{1}{2} 8.16 = 64\) \((m{m^2})\)
\({S_{DKC}}=\dfrac{1}{2}. KC.KD = \dfrac{1}{2}. 22.23 \)\(\,= 253\) \((m{m^2})\)
\({S_{HKDE}}=\dfrac{\left ( HE+KD \right ).HK}{2} \)\(\,= \dfrac{\left (16+23 \right ).18}{2}= 351\) \((m{m^2})\)
Do đó
\({S_{ABCDE}} = {S_{ABC}} + {S_{AHE}} + {S_{DKC}} \)\(\,+ {S_{HKDE}} = 456 + 64 + 253 + 351\)\(\,= 1124\;(m{m^2})\)
Vậy \({S_{ABCDE}} = 1124\;(m{m^2})\)
2. Giải bài 38 trang 130 SGK Toán 8 tập 1
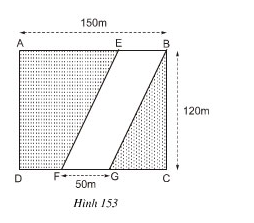
Một con đường cắt một đám đất hình chữ nhật với các dữ liệu được cho trên hình \(153.\) Hãy tính diện tích phần con đường \(EBGF \;(EF // BG)\) và diện tích phần còn lại của đám đất .
Phương pháp giải
- Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó.
\(S = ah\)
- Diện tích hình chữ nhật bằng tích hai kích thước của nó
\( S = a.b\)
(\(S\) là diện tích, \(a\) là chiều dài, \(b\) là chiều rộng của hình chữ nhật).
Hướng dẫn giải
Con đường hình bình hành \(EBGF\) có diện tích là:
\({S_{EBGF}}= 50.120 = 6000\) (\({m^2}\))
Đám đất hình chữ nhật \(ABCD\) có diện tích là:
\({S_{ABCD}}= 150.120 = 18000\) (\({m^2}\))
Diện tích phần còn lại của đám đất:
\(S = {S_{ABCD}} - {S_{EBGF}} = 18000 - 6000 \)\(\,= 12000\;({m^2})\)
3. Giải bài 39 trang 131 SGK Toán 8 tập 1
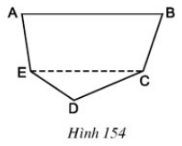
Thực hiện các phép vẽ và đo cần thiết để tính diện tích một đám đất có dạng như hình \(154\), trong đó \(AB // CE\) và được vẽ tỉ lệ \(\dfrac{1}{5000}\)
Phương pháp giải
- Diện tích hình thang bằng một nửa tích của tổng hai đáy với chiều cao.
\(S = {1 \over 2}\left( {a + b} \right).h\)
- Diện tích tam giác bằng nửa tích của một cạnh với chiều cao ứng với cạnh đó.
\(S = {1 \over 2}ah\)
Hướng dẫn giải
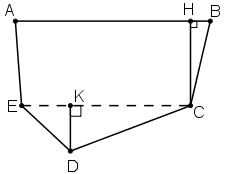
Chia đám đất \(ABCDE\) thành hình thang \(ABCE\) và tam giác \(ECD.\) Cần vẽ đường cao \(CH\) của hình thang và đường cao \(DK\) của tam giác. Thực hiện các phép đo chính xác đến \(mm\) ta được \(AB = 30\,mm, CE = 26\,mm,\) \(CH = 13\,mm, DK = 7\,mm.\)
\({S_{ABCE}}=\dfrac{\left ( AB+EC \right ).CH}{2} \)\(\,= \dfrac{\left ( 30 + 26 \right ).13}{2} =364\) \((m{m^2})\)
\({S_{ECD}}=\dfrac{1}{2} EC. DK = \dfrac{1}{2} .26.7= 91\) \((m{m^2})\)
Do đó \({S_{ABCDE}} = {S_{ABCE}} + {S_{ECD}} = 364 + 91 \)\(\,= 455\) \((m{m^2})\)
Vì bản đồ được vẽ với tỉ lệ xích \(\dfrac{1}{5000}\) nên diện tích đám đất là:
\(S = 455. 5000 = 2275000 \;(m{m^2}) \)\(\,= 2,275 \;({m^2})\)
4. Giải bài 40 trang 131 SGK Toán 8 tập 1
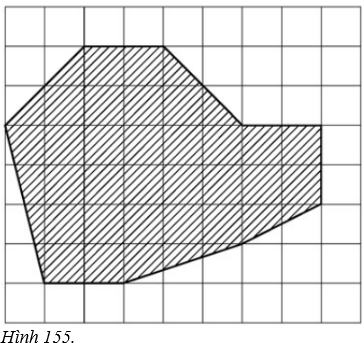
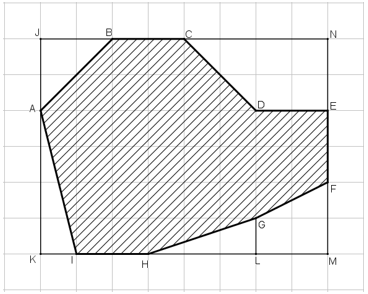
Tính diện tích thực của hồ nước có sơ đồ là phần gạch sọc trên hình \(155\) (cạnh của mỗi hình vuông là \(1\,cm\), tỉ lệ \(\dfrac{1}{10000}\) ).
Phương pháp giải
Ta kẻ thêm hình chữ nhật \(ABCD\), sao cho các cạnh của hình chữ nhật đó đi qua các đỉnh của hồ nước. Sau đó, chia diện tích của hình chữ nhật đó thành diện tích của các tam giác, hình thang và phần diện tích của hồ nước. Áp dụng công thức tính diện tích tam giác, hình thang, hình chữ nhật.
Hướng dẫn giải
Diện tích phần gạch sọc trên hình gồm diện tích hình chữ nhật \(ABCD\) trừ đi diện tích các hình tam giác \(AEN, JKL, DMN\) và các hình thang \(BFGH, CIJK.\) Ta có:
Diện tích hình chữ nhật \(ABCD\) là \( 6. 8=48\) \(cm^2\)
Diện tích tam giác \(AEN\) là \(2\) \(cm^2\)
Diện tích tam giác \(JKL\) là \(1,5\) \(cm^2\)
Diện tích tam giác \(DMN \) là \(2\) \(cm^2\)
Diện tích hình thang \(BFGH\) là \(\dfrac{{\left( {2 + 4} \right).2}}{2} = 6\) \(cm^2\)
Diện tích hình thang \(CIJK\) là \(\dfrac{{\left( {2 + 1} \right).2}}{2} = 3\) \(cm^2\)
Do đó tổng diện tích của các hình tam giác \(AEN, JKL, DMN\) và các hình thang \(BFGH, CIJK\) là:
\(2 + 1,5 + 2 +6 + 3 = 14,5\) \(cm^2\)
Diện tích phần gạch sọc trên hình là:
\(48 - 14,5 = 33,5\) \(cm^2\)
Do tỉ lệ xích \(\dfrac{1}{10000}\) là nên diện tích thực tế là:
\(33,5 . 10000 = 335000\,c{m^2} = 33,5\,{m^2}\)