Giải bài tập SGK Toán 8 Bài 9: Ứng dụng thực tế của tam giác đồng dạng

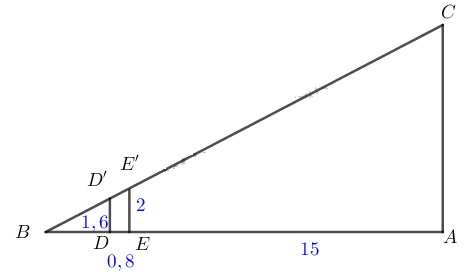
Một người đo chiều cao của một cây nhờ một cọc chôn xuống đất, cọc cao \(2m\) và đặt xa cây \(15m\). Sau khi người ấy lùi ra xa cách cọc \(0,8m\) thì nhìn thấy đầu cọc và đỉnh cây cùng nằm trên một đường thẳng. Hỏi cây cao bao nhiêu, biết rằng khoảng cách từ chân tới mắt người ấy là \(1,6m\)?

Phương pháp giải

Bước 1: Biểu diễn hình học các sự vật theo hình học.

Bước 2: Xét các tam giác đồng dạng, sử dụng tỉ số đồng dạng để tính kích thước cần tính

Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

ΔABC, MN // BC (M ∈ AB, N ∈ AC) ⇒ ΔAMN  ΔABC.

Hướng dẫn giải

Gọi chiều cao của cây là \(AC,\) chiều cao cọc \(EE' = 2m,\) chiều cao từ mắt đến chân người là \(DD' = 1,6m;\) khoảng cách giữa cọc và cây: \(AE = 15m,\) khoảng cách giữa cọc và người đứng: \(DE = 0,8m.\)

Vì \(DD' // EE'\) nên \(ΔBDD' \backsim ΔBEE'\)

\(\Rightarrow \dfrac{BD}{BE} = \dfrac{DD'}{EE'}\)  (cặp cạnh tương ứng tỉ lệ)

\(\Rightarrow 1 - \dfrac{BD}{BE} = 1 - \dfrac{DD'}{EE'}\)

\(\Rightarrow \dfrac{BE - BD}{BE} = \dfrac{EE' - DD'}{EE'}\)

\(\Rightarrow \dfrac{DE}{BE} = \dfrac{2 - 1,6}{2}\)

Hay \(\dfrac{0,8}{BE} = \dfrac{0,4}{2}\)

\(\Rightarrow BE = \dfrac{2.0,8}{0,4} = 4 \, (m)\)

Vì \(EE' // AC\) nên \(ΔEBE' \backsim ΔABC\)

\(\Rightarrow \dfrac{BE}{BA} = \dfrac{EE'}{AC} \) (cặp cạnh tương ứng tỉ lệ)

\(\Rightarrow AC = \dfrac{BA.EE'}{BE}\)

Hay \(AC = \dfrac{EE'(BE + EA)}{BE} = \dfrac{2(4 + 15)}{4} = 9,5 \, (m)\)

Vậy chiều cao của cây là \(9,5m.\)

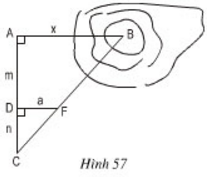
Để đo khoảng cách giữa hai điểm \(A\) và \(B,\) trong đó \(B\) không tới được, người ta tiến hành đo và tính khoảng cách \(AB\) như hình 57; \(AB // DF; \,AD = m;\,DC = n;\, DF = a.\)

a) Em hãy nói rõ cách đo như thế nào.

b) Tính độ dài \(x\) của khoảng cách \(AB.\)

Phương pháp giải

Bước 1: Biểu diễn hình học các sự vật theo hình học.

Bước 2: Xét các tam giác đồng dạng, sử dụng tỉ số đồng dạng để tính kích thước cần tính

Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

ΔABC, MN // BC (M ∈ AB, N ∈ AC) ⇒ ΔAMN  ΔABC.

Hướng dẫn giải

a) Cách đo

- Chọn thêm hai điểm \(D\) và \(C\) sao cho \(A, \,D, \,C\) thẳng hàng và \(AC \bot AB.\)

- Chọn điểm \(B\) sao cho \(C,\, F,\, B\) thẳng hàng và \(DF \bot AC.\)

b) \(ΔCDF \backsim ΔCAB\) (vì \(DE // AB\))

\(\Rightarrow \dfrac{DF}{AB} = \dfrac{CD}{CA}\) (cặp cạnh tương ứng tỉ lệ)

\(\Rightarrow AB = \dfrac{DF.CA}{CD} = \dfrac{a(m + n)}{n} \)

Vậy \(x = \dfrac{a(m + n)}{n}\)

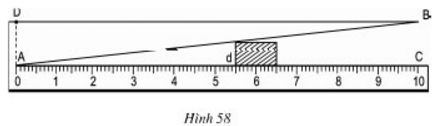
Hình 58 dưới đây mô tả dụng cụ đo bề dày của một số loại sản phẩm. Dụng cụ này gồm thước \(AC\) được chia đến \(1\) mm và gắn với một kim loại hình tam giác \(ABD\), khoảng cách \(BC= 10\) cm.

Muốn đo bề dầy của vật, ta kẹp vật vào giữa bản kim loại và thước (đáy của vật áp vào bề mặt thước \(AC\)), khi đó trên thước \(AC\) ta đọc được bề dày \(d\) của vật (trên hình vẽ ta có \(d=5,5mm\)).

Hãy chỉ rõ định lí nào của hình học là cơ sở để ghi vạch trên thước \(AC\) (\(d ≤ 10\) mm).

Phương pháp giải

Bước 1: Biểu diễn hình học các sự vật theo hình học.

Bước 2: Xét các tam giác đồng dạng, sử dụng tỉ số đồng dạng để tính kích thước cần tính

Nếu một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

ΔABC, MN // BC (M ∈ AB, N ∈ AC) ⇒ ΔAMN  ΔABC.

Hướng dẫn giải

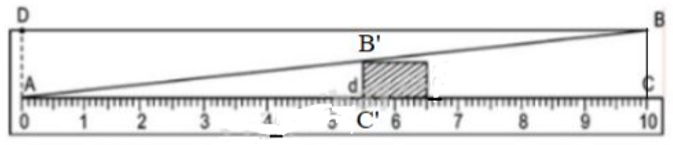
Theo hình vẽ thì \(B'C'//BC\) nên \(∆ABC ∽ ∆AB'C'\) (theo định lí) 

\( \Rightarrow \dfrac{AC'}{AC}= \dfrac{B'C'}{BC}\)

\(B'C'\) là bề dày của vật cần đo 

Vì \(d ≤ 10\) mm nên \(BC=10mm=1cm\)

\( \Rightarrow  B'C' = \dfrac{AC'. BC}{AC}= \dfrac{1}{10}AC'\)

Vậy khi \(AC' = 5,5 \,cm\) thì đọc \(B'C' = \dfrac{1}{10}.  5,5\, cm\)\(=0,55cm = 5,5\, mm.\)

Dụng cụ trên đã dùng tính chất hai tam giác đồng dạng thì cạnh tương ứng tỉ lệ.