Giải bài tập SGK Toán 8 Bài 3: Thể tích của hình hộp chữ nhật

1) Gấp hình 87a theo các nét đã chỉ ra thì có được một hình hộp chữ nhật hay không?

2) Kí hiệu các đỉnh hình hộp gấp được như 87b.

a) Đường thẳng BF vuông góc với những mặt phẳng nào?

b) Hai mặt phẳng (AEHD) và (CGHD) vuông góc với nhau, vì sao?

Phương pháp giải

Dựa vào lý thuyết về đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc với nhau.

+ Một đường thẳng vuông góc với một mặt phẳng nếu nó vuông góc với hai đường thẳng cắt nhau trong mặt phẳng đó.

+ Hai mặt phẳng được gọi là vuông góc nếu có một đường thẳng nằm trong mặt phẳng này và vuông góc với mặt phẳng còn lại. 

Hướng dẫn giải

1) Gấp hình 87a  theo các nét đã chỉ ra thì ta được một hình hộp chữ nhật.

2)

a) Trong hình hộp \(ABCD.EFGH\) thì:

+) BF vuông góc với hai đường thẳng cắt nhau EF và FG của mặt phẳng (EFGH) nên BF vuông góc với mặt phẳng (EFGH).

+) BF vuông góc với hai đường thẳng cắt nhau AB và BC của mặt phẳng (ABCD) nên BF vuông góc với mặt phẳng (ABCD).

b) Hai mặt phẳng \((AEHD)\) và \((CGHD)\) vuông góc với nhau vì mặt phẳng \((AEHD)\) chứa đường thẳng \(EH\) vuông góc với mặt phẳng \((CGHD)\) tại \(H\). 

a) Tính các kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với \(3,\, 4,\, 5\) và thể tích của hình hộp này là \(480 cm^3\).

b) Diện tích toàn phần của một hình lập phương là \(486 m^2\). Thể tích của nó bằng bao nhiêu?

Phương pháp giải

a) Áp dụng công thức tính thể tích hình hộp chữ nhật : \(V = a.b.c\), trong đó \(a,\, b,\, c\) là ba kích thước của hình hộp chữ nhật. Sau đó áp dụng tính chất của tỉ lệ thức để tìm \(a,\, b,\, c\).

b) Diện tích toàn phần = diện tích một mặt \( \times 6\)

Do đó,  diện tích một mặt = diện tích toàn phần \( :  6\)

Lập luận để tìm độ dài cạnh hình lập phương.

Áp dụng công thức tính diện tích hình lập phương : \( V = a^3\).

Hướng dẫn giải

a) Gọi \(a,\, b,\, c\) là ba kích thước của hình hộp chữ nhật.

Vì \(a,\, b,\, c\) tỉ lệ với \(3,\, 4,\, 5\) nên

\(\dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5}= t \;  ( t > 0)   \) 

\(\Rightarrow  a = 3t;\; b = 4t;\; c = 5t  \quad (1) \)

Mà thể tích hình hộp là \( 480cm^3\) nên \(a.b.c = 480 \quad  (2)\)

Từ (1) và (2) suy ra 

\( 3t.4t.5t = 480 \Rightarrow 60t^3 = 480\)

\(  \Rightarrow t^3 = 8 \Rightarrow t = 2 \) 

Do đó:

\(a =3t=3.2= 6(cm);\\ b=4t=4.2 = 8(cm); \\ c=5t=5.2 = 10 (cm) \)

Vậy các kích thước của hình hộp là \(6cm;\; 8cm; \; 10cm\) .

b) Hình lập phương là hình có \( 6\) mặt là các hình vuông bằng nhau.

Diện tích một mặt là:

\(486 : 6 = 81 (cm^2) \)

Gọi \(a\) là độ dài cạnh hình lập phương, ta có:

\(a^2=81\)

Suy ra độ dài cạnh hình lập phương là  \( a = \sqrt{81}=9\, (cm) \).

Thể tích hình lập phương là :    \( V = a^3 = 9^3 = 729 (cm^3)  \).

 \(A,\, B,\, C \) và \(D\) là những đỉnh của hình hộp chữ nhật cho ở hình 88.

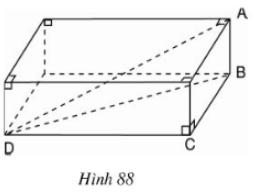
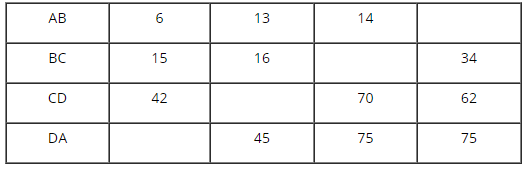
Hãy điền số thích hợp vào các ô trống ở bảng sau:

Kết quả bài 12 minh họa công thức quan trọng sau:

\(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

Phương pháp giải

- Áp dụng định lý Py-ta-go trong tam giác vuông để chứng minh công thức: 

\(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

- Áp dụng công thức bên trên để tìm độ dài các đoạn thẳng chưa biết.

Hướng dẫn giải

Trước hết ta chứng minh hệ thức sau: \(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

Ta có:  \( \triangle BCD\) vuông tại \( C \Rightarrow  BD^2  = DC^2 + BC^2\)

 \( \triangle ABD\) vuông tại \(B \Rightarrow  AD^2  = BD^2 + AB^2\)

\( \Rightarrow AD^2 = DC^2 +BC^2 + AB^2 \)

Suy ra:  \(DA = \sqrt{AB^{2}+BC^{2}+CD^{2}}\)

Áp dụng hệ thức này ta sẽ tính được độ dài  một cạnh khi biết  ba độ dài kia.

Cột 1: \(AB=6,BC=15, CD=42\)

\(DA = \sqrt {{6^2} + {{15}^2} + {{42}^2}}  = \sqrt {2025}  \)\(\,= 45\)

Cột 2: \(AB=13,BC=16,DA=45\)

\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow C{D^2} = D{A^2} - A{B^2} - B{C^2} \cr
& \Rightarrow CD = \sqrt {D{A^2} - A{B^2} - B{C^2}} \cr
&= \sqrt {{{45}^2} - {{16}^2} - {{13}^2}} \cr
&= \sqrt {1600} = 40 \cr} \)

Cột 3: \(AB=14,CD=70,DA=75\)

\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow B{C^2} = D{A^2} - A{B^2} - C{D^2} \cr
& \Rightarrow BC = \sqrt {D{A^2} - A{B^2} - C{D^2}} \cr
&= \sqrt {{{75}^2} - {{14}^2} - {{70}^2}} \cr
&= \sqrt {529} = 23 \cr} \)

Cột 4: \(BC=34,CD=62,DA=75\)

\(\eqalign{
& D{A^2} = A{B^2} + B{C^2} + C{D^2} \cr
& \Rightarrow A{B^2} = D{A^2} - B{C^2} - C{D^2} \cr
& \Rightarrow AB = \sqrt {D{A^2} - B{C^2} - C{D^2}} \cr
&= \sqrt {{{75}^2} - {{34}^2} - {{62}^2}} \cr
&= \sqrt {625} = 25 \cr} \)

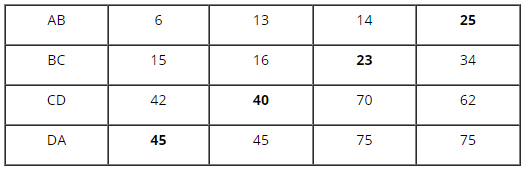
Do đó ta có kết quả như bảng dưới đây:

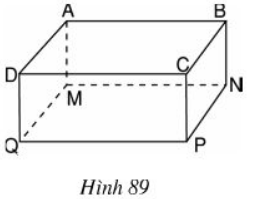
a) Viết công thức tính thể tích của hình hộp chữ nhật \(ABCD.MNPQ\) (h.89).

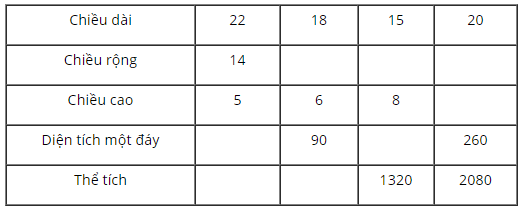
b) Điền số thích hợp vào các ô trống ở bảng sau:

Phương pháp giải

a) Áp dụng công thức tính thể tích hình hộp chữ nhật: \(V = a.b.c\), trong đó \( a,\, b, \, c\) là các kích thước của hình hộp chữ nhật;

Hay thể tích = chiều dài \( \times\) chiều rộng \( \times\) chiều cao.

b) Giả sử \( a\) là chiều dài, \( b\) là chiều rộng và \(  c\) là chiều cao. 

Ta áp dụng các công thức sau:

\(V = a.b.c\)

\(b= V :( a.c)\)

\( S_{\mbox{1 đáy}} = a.b\)

\(b = S_{\mbox{1 đáy}}: a\)

\(c= V :S_{\mbox{1 đáy}}\)

Hướng dẫn giải

a) \({V_{ABCD.MNPQ}} = MN.{\rm{ }}NP.{\rm{ }}NB\)

b) 

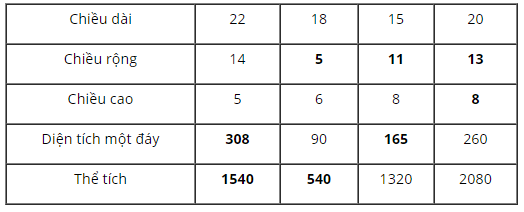
+ Hình hộp chữ nhật với các kích thước ở cột 1: 

Diện tích một đáy là: \(22 . 14 = 308\)  

Thể tích là: \(22. 14 . 5 = 1540\)

+ Hình hộp chữ nhật với các kích thước ở cột 2:

Chiều rộng là: \(90 : 18 = 5\)

Thể tích là: \(18 . 5 . 6 = 90 . 6 = 540\)

+ Hình hộp chữ nhật với các kích thước ở cột 3:

Chiều rộng là: \(1320 : (15 . 8) = 11\)

Diện tích một đáy là: \(15 . 11 = 165\)

+ Hình hộp chữ nhật với các kích thước ở cột 4:

Chiều rộng là: \(260 : 20 = 13\)

Chiều cao là: \(2080 : 260 = 8\)

Ta có kết quả chung như bảng sau: