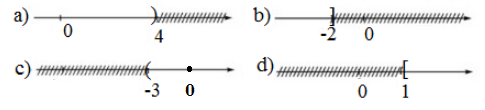Giải bài tập SGK Toán 8 Bài 3: Bất phương trình một ẩn

Kiểm tra xem giá trị \(x = 3\) là nghiệm của bất phương trình nào trong các bất phương trình sau:

a) \(2x + 3 < 9\)

b) \(-4x > 2x + 5\)

c) \(5 - x > 3x - 12\)

Phương pháp giải

Áp dụng định nghĩa: Nghiệm của bất phương trình là giá trị của ẩn thay vào bất phương trình ta được một khẳng định đúng.

Hướng dẫn giải

Câu a

Thay \(x = 3\) vào bất phương trình ta được: \(2.3 + 3 < 9\) \( \Rightarrow 9 < 9\) (khẳng định sai)

Vậy \(x = 3\) không là nghiệm của bất phương trình \(2x + 3 < 9\)

Câu b

Thay \(x = 3\) vào bất phương trình ta có: \(-4.3 > 2.3 + 5  \Rightarrow  -12 > 11\) (khẳng định sai)

Vậy \(x = 3\) không là nghiệm của bất phương trình \(-4x > 2x + 5\).

Câu c

Thay \(x = 3\) vào bất phương trình ta có: \(5 - 3 > 3.3 -12 \Rightarrow  2 > -3\) (khẳng định đúng)

Vậy \(x = 3\) là nghiệm của bất phương trình \(5 - x > 3x - 12\).

Viết và biểu diễn tập nghiệm trên trục số của mỗi bất phương trình sau:

a) \(x < 4\);          b) \(x ≤ -2\);           c) \(x > -3\);              d) \(x  ≥ 1\).

Phương pháp giải

Áp dụng qui tắc biểu diễn tập nghiệm trên trục số.

Hướng dẫn giải

\(\eqalign{
& a)\,\,\,S = {\rm{\{ }}x|x < 4\} \cr
& b)\,\,\,S = {\rm{\{ }}x|x \le - 2\} \cr
& c)\,\,\,S = {\rm{\{ }}x|x > - 3\} \cr
& d)\,\,S = {\rm{\{ }}x|x \ge 1\} \cr} \) 

Biểu diễn các tập nghiệm trên trục số: 

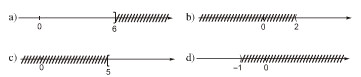
Hình vẽ sau đây biểu diễn tập nghiệm của bất phương trình nào? (Chỉ nêu một bất phương trình).

Phương pháp giải

Áp dụng qui tắc biểu diễn tập nghiệm của phương trình trên trục số.

Hướng dẫn giải

a) Hình a biểu diễn tập nghiệm của bất phương trình \(x ≤ 6\).

b) Hình b biểu diễn tập nghiệm của bất phương trình \(x > 2\).

c) Hình c biểu diễn tập nghiệm của bất phương trình \(x ≥ 5\). 

d) Hình d biểu diễn tập nghiệm của bất phương trình \(x < -1\).

Hãy lập bất phương trình cho bài toán sau:

Quãng đường đi từ A đến B dài \(50\)km. Một ô tô đi từ A đến B, khởi hành lúc \(7\) giờ. Hỏi ô tô phải đi với vận tốc bao nhiêu km/h để đến B trước \(9\) giờ cùng ngày?

Phương pháp giải

Áp dụng bài toán: thời gian = quãng đường : vận tốc.

- Đặt vận tốc của ô tô làm ẩn, biểu diễn thời gian ô tô đi từ A đến B theo ẩn đó.

- Đặt điều kiện cho ẩn để tìm được bất phương trình cần tìm.

Hướng dẫn giải

Gọi \(x\) là vận tốc của ô tô (\(x > 0\), tính bằng km/h)

Thời gian ô tô đi từ A đến B là: \( \dfrac{50}{x}\) (giờ)

Thời gian từ \(7\) giờ đến \(9\) giờ là: \(9 - 7 = 2\) giờ.

Để đến B trước \(9\) giờ thì \( \dfrac{50}{x} < 2\)

\(⇔ 50 < 2x\) (nhân cả hai vế với x > 0)

\(⇔ 25 < x\) (chia cả hai vế cho 2).

Vậy để ô tô đến B trước 9 giờ thì ô tô phải chạy với vận tốc x thỏa mãn: \(x > 25\) (km/h)